|
ようこそ、化学標準物質の不確かさへのいざない |
アーカイブ（統計処理ソフト）
「不確かさ」にはAタイプの不確かさとBタイプの不確かさがあり、Aタイプの不確かさは純粋に統計学的に求めることができる量です。そこで、ここではAタイプの不確かさを求めるための統計処理ソフトを紹介します。
「Aタイプの不確かさ」は統計で言うところの「母分散
」の正の平方根、すなわち、「母標準偏差
」に相当し、統計学における分散分析や回帰分析などで算出可能な量です。
「分散分析」は統計処理のモデルによって、いろいろな分析法があるが、ここでは化学標準物質の調製濃度のバラツキやアンプル詰めをしたときのアンプル間バラツキを決定するための統計処理モデルとしてよく使用される「枝分かれ実験（nested design）」（変量型因子モデル）の分散分析についての統計処理ソフトをまず紹介します。
下記の例は「二段枝分かれ実験」（２因子実験モデルの中の変量型因子モデルで、下段の因子が上段の因子にネストしているモデル）分散分析の例です。この場合は、質量比混合法で
種の標準液を調製し、それぞれの調製液から
種のアンプルをランダムに小分けして、得られたアンプル溶液の濃度につき
回の繰り返し測定を行った例（図１参照）を想定しています。すなわち、調製液は基準液を一定組成になるようできるだけ精密に秤量して調製した液であるので、各調製液はランダムサンプリングした標本と見なされることから変量型であり、またアンプルはこれらの各調製液からランダムに小分けしたものであるからこれも変量型であり、「二段枝分かれ実験」分散分析の典型例と考えられます。
このように２因子がネストしている２因子変量型モデル（無作為抽出標本モデル）に対して、２因子がクロスしている場合は、通常「繰り返しのある二元配置実験」の分散分析を行うことになります。すなわち、ある標準液の
番目のアンプルと別の標準液の番目のアンプルとは何の因果関係もないような変量モデルの場合は「二段枝分かれ実験」分散分析を行い、ある標準液の番目のアンプルと別の標準液の番目のアンプルとは同じアンプルを使って小分けしたので両者の間には因果関係があるような構造モデル
では「繰り返しのある二元配置実験」分散分析を行うことになります。「繰り返しのある二元配置実験」モデルの中には、「２因子実験変量モデル」と「２因子実験母数モデル」、あるいはそれら母数型因子と変量型因子が混合した「２因子実験混合モデル」があります。いずれのモデルでも上述の構造モデル式は同じであり、
は因子
の主効果、
は因子
の主効果を表し、
は２因子の交互作用
の項（単に
と表すこともあります）を表します。しかしながら、それぞれの変動要因との不偏分散の期待値はモデルによって異なりますが、交互作用の不偏分散の期待値（
）と誤差変動
の不偏分散の期待値（
）はモデルによって変わりません。ところで、交互作用の不偏分散が誤差変動の不偏分散に比較して小さい（交互作用がほとんどない）場合には、交互作用を誤差変動にプールした構造モデル
を使って統計分析をする方が、誤差変動の自由度が大きくなるため、一般に主効果
の検定精度が上がり、また合意値
（すなわち総平均
）の不確かさも小さくなります。ちなみに、「２因子実験母数モデル」の因子の不偏分散、因子の不偏分散、交互作用、誤差変動の期待値は
であり、因子、因子、交互作用、誤差変動の自由度は
です。これに対し、「２因子実験変量モデル」の因子の不偏分散、因子の不偏分散、交互作用、誤差変動の期待値は
であり、「２因子実験母数モデル」とは異なり、期待値だけでなく、主効果や主効果の
検定量も変わることに注意して下さい。「２因子実験混合モデル」では当然のことですが上述の二種類の期待値の混合型になります。
ところで、「２因子実験母数モデル」において、交互作用が小さくて誤差に交互作用をプールした場合の各変動要因、自由度、不偏分散の期待値は
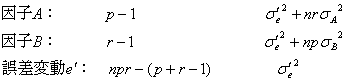
となります。このプーリングした「繰り返しのある二元配置実験」の構造モデル式
は、次に詳述する「二段枝分かれ実験」の構造モデル式と見かけ上ちょっと似ていますが、それらの変動要因の自由度や不偏分散の期待値は全く異なりますので注意する必要があります。また、「繰り返しのない二元配置実験」は
なので誤差変動の自由度が
になり、結果として交互作用の項は消失し誤差変動に変わり、構造モデル式は
。
のような単純なモデルで表され、各変動要因、自由度、不偏分散の期待値は
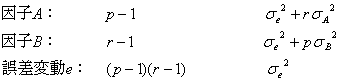
となります。
さて、話を本題に戻して、「二段枝分かれ実験」では、図２のような構造モデル
を仮定し、枝分かれ分散分析を行うことにより、図３に示されるような分散分析表（ANOVA）からそれぞれの誤差変動要因の分散（
）の推定値（
）を求めることができます。これらの分散の推定値の和の平方根をとれば、それがこの被検溶液の濃度測定データ１個（
）当たりのAタイプの標準不確かさ(
) になります。
Aタイプの標準不確かさ 
また、この被検溶液の濃度測定データの総平均（）のAタイプの標準不確かさ() は
Aタイプの標準不確かさ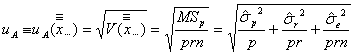 
のようになります。ただし、測定データの総平均（）は
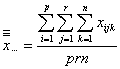
です。
もし、この他の情報として、Bタイプの標準不確かさ（
）が見積もられる場合（Bタイプの拡張不確かさ
が既知の時には、包含係数（通常
とする）を使って、
の式から見積もることが可能）には、この系の拡張不確かさ（
）は合成標準不確かさ（
）に包含係数（）を掛けて求めることができます。
合成標準不確かさ 
拡張不確かさ 
ちなみに拡張不確かさ（）というのは、測定対象となる標本の総平均をとした時、母平均（
）が包含係数（）に相当する確率（の場合は、ほぼ95%の確率）で区間 
、すなわち、
に入っていることを意味します。つまり
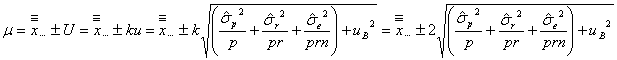
となります。もちろん、Bタイプの不確かさがなければ母平均は
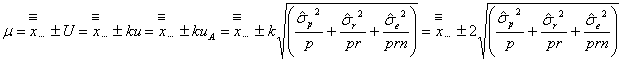
となります。以降、Bタイプの不確かさを無視し、包含係数はとして話を進めます。
一方、標準液の濃度そのものよりも質量比混合法で標準液を調製したときの調製バラツキや調製液をアンプルに小分けしたときのアンプル間バラツキに関心がある場合は、二段枝分かれ分散分析によって求められた各分散成分の推定値
や
の値から、それらの変動による不確かさを見積もることになります。すなわち、調製バラツキによる不確かさを
、アンプル小分けのアンプル間バラツキの不確かさを
とすれば
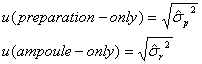
となります。これら２つの不確かさは被検溶液の無作為抽出（random sampling）に基づく不確かさなので、この不確かさを
とすれば
となります。また、繰り返し測定の偶然誤差に基づく測定バラツキの不確かさを
とすれば
ですから、先述の被検溶液の濃度測定データ１個（）当たりのAタイプの標準不確かさ()は
のように、サンプリング・バラツキと測定バラツキの和の正の平方根と見ることもできます。
標準液の表示値として質量比混合法で調製した標準液から小分けしたアンプル１本の表示値は、その標準液の調製値
（固定値）をそのまま使うというのであれば
のようになります。
しかしながら、標準液の表示値として質量比混合法で調製した標準液から小分けしたアンプル１本の表示値は、その標準液の調製値（固定値）を使うのではなく、濃度測定の結果得られた総平均値（確率変数
の実現値の一つ）を使うというのであれば
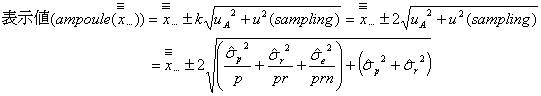
となります。すなわち、このようなアンプル１本のもつ不確かさは総平均値を求めるのに伴う不確かさとサンプリングの不確かさを合成したものになるのです。ここで、総平均値を求めるのに伴う不確かさは、別の見方をすれば、標準液（母液）の母平均をとしたとき、その母平均の推定値
として総平均値を採択したという意味（逆に言えば
）なので、不確かさは標準液（母液）の濃度を総平均値としたときの標準液（母液）の濃度の持つ不確かさ
であり、
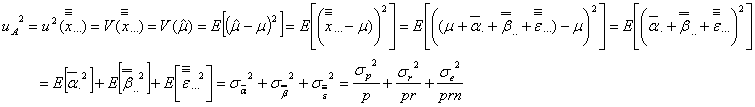
となります。
一方、アンプル１本（調製液
から小分けした
番目のアンプル）の母平均を
とすれば
であるから、アンプル１本の表示値（母平均の推定値
）として総平均値を採択すれば、アンプル１本の持つ不確かさの分散
は
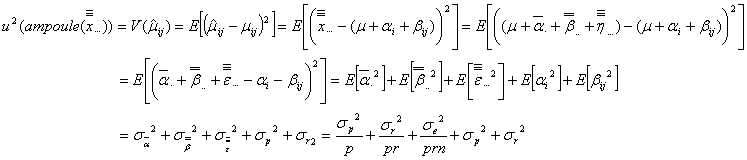
となります。したがって、濃度測定の結果得られた総平均値をアンプル１本の表示値として使うのであれば、不確かさを併記したアンプル１本の表示値は
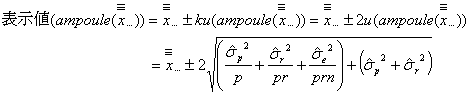
となり、前述の
の導出式と一致します。
また、標準液の表示値として質量比混合法で調製した標準液から小分けしたアンプル１本の表示値として、その標準液の調製値（固定値）をそのまま使うというのであれば、上と同様な考え方で、アンプル１本の表示値（母平均の推定値）として標準液の調製値
を採択したことになるので、アンプル１本の持つ不確かさの分散
は
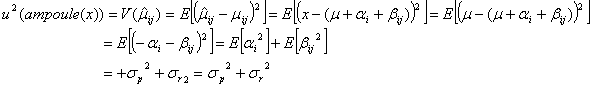
となります。したがって、調製値（固定値）をアンプル１本の表示値として使うのであれば、不確かさを併記したアンプル１本の表示値は
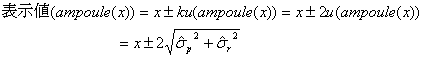
となり、前述のだけを考慮した
の導出式と一致します。
このように、アンプル１本の表示値として標準液（母液）の調製値（固定値）を使う場合は、アンプルの表示値の不確かさはサンプリングの不確かさのみの不確かさ
になるが、同じアンプル１本の表示値として測定値（確率変数の実現値の一つ）を採択した場合（このような例は実際問題としてはあまりないとは思いますが・・・、ただ品質管理を行う過程での抜き取り検査ではあり得るケースです）のアンプル１本の不確かさの分散
は
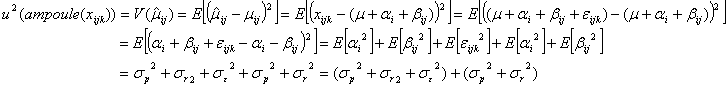
となり、したがって、
は
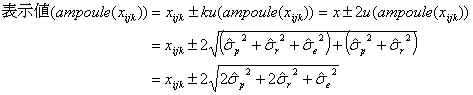
となります。すなわち、アンプル１本の表示値として測定値（確率変数の実現値の一つ）を採択した場合のアンプル１本の不確かさは、測定値を求めるのに付随する不確かさ成分
と標準液（母液）を新たに調製して得られる調製液からアンプルに小分けしたときのサンプリングによる不確かさ
の和になっていることがわかります。
なお、以下の図では、簡単のために総平均値
を単にと書き表し、
および
はそれぞれ
および
と書き表わしました。
枝分かれ実験分散分析
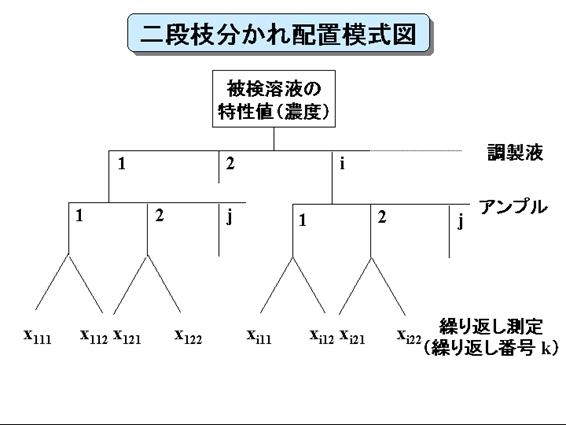
図１
図２
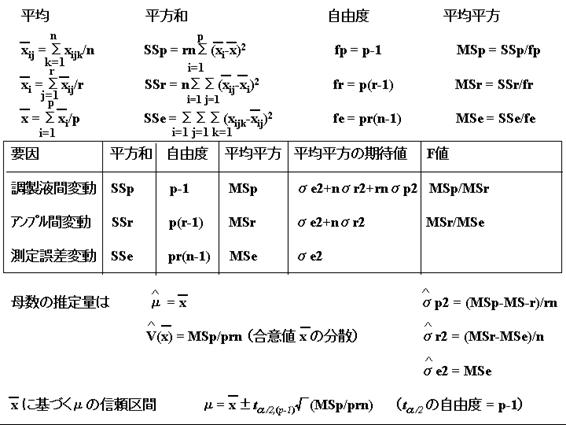
図３
上図のような枝分かれ分析を一段枝分かれから四段枝分かれまで自動化したexcelマクロファイルを以下に載せたので、自由にダウンロードして使ってみて下さい。
なお、「一段枝分かれ分析」については当然のことながら、Excelの標準ツールである統計処理のための分析ツールの「分散分析：一元配置」と同じ結果を与えることになります。ただし、Excelの分析ツールでは分散は自動算出できず手計算をしなければなりませんが、このマクロでは不確かさまで自動計算できるようになっています。
旧バージョンは「欠測データ」の処理はできませんが、データ数が少ない場合は使いやすいと思います。それ以外のバージョンは欠測処理が自動でできるようになっています。
（参考文献： 「欠測データ」の扱いについては奥野忠一，「応用統計ハンドブック」，養賢堂，第1冊第9版，p. 252(1999)を参照）
ExcelのSheet1にあるデータシートのデータ値を統計処理ソフトSPSS用フォーマットに書き換えたり、逆にSPSS形式のデータ値をExcelのSheet1上のデータシートに読み込んだりすることができるようになっています。
下記のマクロファイルを使用するに当たっては、「欠測データ」のセルには空白文字は入れないようにして下さい。見かけ上、そのようなセルは空に見えても、空白文字が入っている場合は計算ミスが生じます。しっかりDELETEキーでセル内容を消してから統計処理を行って下さい。
JCSS対応（Windows専用）旧バージョン
JCSS対応（Windows専用）
JCSS対応（Windows,Macともに稼動）
一般的な分散分析（Windows,Macともに稼動）
（補足説明）上掲の「一般的な分散分析」マクロの解析結果の表示（Sheet２）において、拡張不確かさを求めるための「有効自由度」が算出されていますが、厳密に算出してみてもあまり意味がない場合も多いので、分散成分あるいは合成標準不確かさについての計算結果を用いて、簡単に包含係数をとした拡張不確かさを求めることもよくあります。
ISO GUIDE 35:2006(E) 7.9 Insufficient repeatability of the measurement methodを考慮した分散分析（Windows,Macともに稼動）
（補足説明）上掲の「二段枝分かれ分析マクロ v9.1」においては、二段目の要因による変動が他の要因に比べて無視できるほど小さい場合は、プーリングを行って「一段枝分かれ分析」ができるようにマクロの更新を行いました。実際のやり方は、通常通り「二段枝分かれ分析マクロv9.1」の「解析」ボタン処理を行う前に、まず「SPSS」ボタンを押して二段枝分かれ分析」に使うデータをSheet3にSPSS準拠フォーマットのデータとして貼り付けます。その後、上記「解析」ボタンを押すと、Sheet2には通常の「二段枝分かれ分析」の計算結果が、またSheet5には二段目の要因による変動を測定誤差変動にプーリングしたデータ（「一段枝分かれ分析」に相当）が表示され、同時にSheet3のデータの中でB列を除いたものがSheet7に貼り付けられ、プーリングしたデータについての計算結果がSheet6に表示されます。
回帰分析
重み付き回帰分析（Deming法）マクロにおいては、座標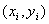
の重み
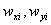は
で定義することにします。ここで、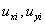
は変数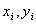
の「標準不確かさ」であり、
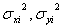は母分散、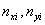
は観測データの数です。したがって、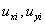は統計学で言うところの「標準誤差」に相当する量になります。もちろん、観測データ数が
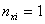や
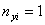のときは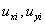は「標準偏差」に相当する量になります。
１次回帰式（原点を通らない回帰直線）
y = a + bx
回帰分析の中でも実際に最もよく遭遇する例は直線回帰であろうと思われます。また直線回帰には、原点（
）を通る特殊な回帰直線と
軸に切片
を持つより一般的な回帰直線（
）がありますが、ここでは後者のマクロをまず紹介することにします。
また、このマクロでは
に対応する測定点
が個の繰り返し測定からなっているものと仮定しています。
マクロv2.71は繰り返しのない（
）回帰分析もエラー表示することなく処理できるプログラムです。いずれのマクロも独立変数には不確かさはなく従属変数にのみ標準不確かさがあることを仮定しており、その不確かさの分散はの値によって変化せず正規母集団分布をしているものと仮定しています。このような仮定は回帰直線に乗る測定データについては多くの場合当てはまります。
重み付き回帰分析（Windows専用）の重み付き回帰分析wマクロはDemingの簡略法による重み付き直線回帰分析のプログラムです。初期条件として独立変数と従属変数の分散
と
の比
の逆数（
）である重みを入力する必要があります。ただし厳密な値を入力する必要はなくおよその値で十分です。
また、重み付きDeming回帰分析wdマクロv1.3は独立変数
と従属変数
のどちらにも不確かさ
があり、しかもの値によって異なるような複雑な系について線形回帰分析ができる応用性の高いマクロです。重み付きDeming回帰分析wdマクロv2.3およびv2.4は、サブルーチンの内容を書き換えればのような線形のみならず非線形回帰曲線
のあてはめにも対応可能なマクロです。ただし、あてはめ可能なパラメータの数は標本データ（
）の総数
以内です。もちろん、指数関数を対数形に変換したものがこの多項式になる場合は、変換プログラムをサブルーチン
（観測方程式を表現するサブルーチン）内に書き加えれば、指数関数や対数関数の回帰分析にも対応可能です。
JCSS対応（Windows専用）
一般的な回帰分析（Windows専用）
ISO GUIDE 35:2006(E) 7.9 Insufficient repeatability of the measurement methodを考慮した回帰分析（Windows専用）
重み付き回帰分析（Windows専用）
下記の三段枝分かれ実験回帰分析のマクロは、一段目の変動要因が日間変動のような経時変化である場合、その変動（たとえば特定標準液の保存安定性）が回帰直線に乗っていると仮定した場合の測定データの不確かさを、通常の枝分かれ実験分散分析の不確かさと比較しながら算出するプログラムです。詳細は本ホームページの分散分析の「三段枝分かれ実験分散分析と経時変化に１次回帰を考慮したケース」を参照して下さい。
枝分かれ実験回帰分析（Windows専用）
比例回帰式（原点を通る回帰直線）
y=bx
一般的な比例回帰分析（Windows専用）
原点（）を通る回帰直線のことを比例回帰式とも言いますが、ここではそのようなマクロをいくつか掲載しておきます。一般的な比例回帰分析は、繰り返し測定を行った標本の全データの
個の組
（ただし、
（繰り返し測定数）とする）
をそのまま使いますが、推定回帰直線は必ず原点（）を通る回帰直線（
）であることを仮定しています。
回帰分析0マクロV.1.0 （原点を通る回帰直線分析自動計算システム）
重み付き比例回帰分析（Windows専用）
次に紹介するマクロは、上記と同じく原点（）を通る回帰直線（）ですが、繰り返し測定データの組
（ただし、（繰り返し測定数）とする）の最初のデータの組の平均
が原点
を通るように座標変換した新たな測定データの
個の組
を用いて比例回帰分散するマクロです。ただし、原点のデータ（
に相当するデータ
）は諸パラメータの算出に当たっては使用しません。したがって、総データ数は
となります。
回帰分析00マクロV.1.0 （座標変換した原点を通る回帰直線分析自動計算システム）
２次関数（原点を通らない回帰曲線）
y = a + bx + cx2
このマクロではに対応する測定点が個の繰り返し測定からなっているものと仮定しています。もちろんのデータも処理できます。回帰分析wdp2
v1.0 （重み付き多項式Deming回帰分析自動計算システム）は、独立変数と従属変数のどちらにも不確かさがあり、しかもの値によって異なるような複雑な系について線形回帰分析ができるマクロです。ただし、このマクロの計算結果には比較のために１次式直線回帰分析の結果も併せて出力するようになっています。,
重み付き回帰分析（Windows専用）
回帰分析wdp2マクロv1.0 （重み付き多項式Deming回帰分析自動計算システム）
３次関数（原点を通らない回帰曲線）
y = a + bx + cx2 + dx3
このマクロではに対応する測定点が個の繰り返し測定からなっているものと仮定しています。もちろんのデータも処理できます。回帰分析wdp3
v1.0 （重み付き多項式Deming回帰分析自動計算システム）は、独立変数と従属変数のどちらにも不確かさがあり、しかもの値によって異なるような複雑な系について線形回帰分析ができるマクロです。ただし、このマクロの計算結果には比較のために１次式直線回帰分析の結果も併せて出力するようになっています。,
重み付き回帰分析（Windows専用）
回帰分析wdp3マクロv1.0 （重み付き多項式Deming回帰分析自動計算システム）
多項式回帰曲線応用例１（動粘度と温度）
logX = a – blogY
重み付き回帰分析（Windows専用）
回帰分析wda1マクロv1.0 （重み付き多項式Deming回帰分析自動計算システム）
多項式回帰曲線応用例２（指数関数）
Y = aebX
重み付き回帰分析（Windows専用）
回帰分析wda2マクロv1.0 （重み付き指数関数式Deming回帰分析自動計算システム）
多項式回帰曲線応用例３（円の方程式）
(x-a)2 + (y-b)2 = r2
重み付き回帰分析（Windows専用）
回帰分析wda3マクロv1.0 （重み付き多項式Deming回帰分析自動計算システム）