|
ようこそ、化学標準物質の不確かさへのいざない |
分散分析
分散分析はAタイプの不確かさ（統計処理）を求めるための最も基本となる統計処理です。そこで、ここでは分散分析の基本と分散分析による不確かさの求め方を解説します。
母集団が無限正規母集団でそこから無作為抽出をしたデータ構造のない標本については、推測統計学の最も基本的で簡単な統計処理により、その標本の不確かさを求めることができます。すなわち、いま無限正規母集団
から無作為抽出した標本のデータを
と仮定すれば、標本の平均と分散は
のようになり、それらの期待値
および
は
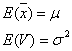
なので、それぞれ正規母集団の母平均
と母分散
になります。したがって、標本のデータ１個当たりの標準不確かさ
は母標準偏差
に等しいから
となります。ここで、
は母標準偏差の推定値で、標本の不偏標準偏差
に等しい値です。また、標本平均
の標準不確かさ
については
のようになります。不確かさは通常これらの標準不確かさ
に包含係数
を掛けた拡張不確かさ
で表されますので
となります。ここで、包含係数はスチューデントの
分布の値
と同じく
の関係式から求められますが、通常危険率
を5%（したがって信頼率
は約95%）とした値に近いもの（標本数が十分に大きい場合（
）には
）として、わざわざスチューデントの分布の値を求めることなく、
とする場合が多いようです。したがって、拡張不確かさを記載する場合には必ず包含係数の値を併記する必要があります。
次に、標本データに構造がある場合（構造模型）には、「分散分析」により不確かさを求めることになります。いま、２元配置実験において、因子Aの水準数が
個（
）および因子Bの水準数が
個（
）の場合、条件
での測定値を
とすれば、この値は
で表すことができます。ここで、ギリシャ文字で記された 各文字はそれぞれ次のように呼ばれる母数または変量です。
因子
や
の水準
や
はあらかじめ決められた処理である場合が多いが、場合によっては多数の処理からランダムに選ばれた理であることもあり、後者の場合は母集団からの標本抽出ごとに異なる処理となります。したがって、前者の因子やは「母数型」であり、後者の因子やは「変量型」であると言われます。いずれにしても、このような構造模型では、（１）
は正規分布に従うこと（正規性の仮定）、（２）各
の分散は等しいこと（等分散性の仮定）、（３）各
は互いに独立であること（独立性の仮定）が成立していなければなりません。このような条件の下で、帰無仮説
など、主効果や交互作用の有無を検定することを分散分析と言います。
そこで、分散分析の中でも最も簡単な一元配置実験についてまず取り上げることにします。この構造模型では因子はただ一つ（これをとし、その水準数を個とします）であり、なる水準の下での
回目の測定値（測定の繰り返し数は
とします）としてというデータが得られたすれば、構造模型は
であり、水準の効果
は
を
番目の水準の平均としたとき
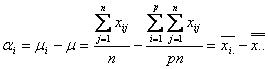
となります。したがって、
という関係が成立します。因子の主効果の不偏分散を
とすると
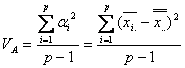
となります。一方、偶然誤差
は
なので、その偶然誤差の不偏分散を
とすると
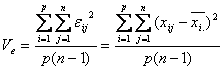
となります。不偏分散との期待値
および
は、それぞれに対応する分散を
および
とすれば
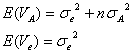
となります。一元配置分散分析の帰無仮説は
であるので、をに対して検定することになります。したがって、その比である
値
を検定すれば主効果があったのかどうかを検定することができます。検定に使う分布の右片側検定点は
であり、検定は上述の値とこの有意水準点
と比較検定することになります。もし
ならば、帰無仮説を棄却して対立仮説
を採択することになり、因子の主効果があったということになります。また、逆に
ならば、帰無仮説は棄却できず測定データには因子の主効果はなかったという結論になります。ここで、主効果がある場合の総分散をとすれば
となります。次表は分散分析でよく使われる分散分析表（ANOVA）です。
データ１個の期待値
と分散
は
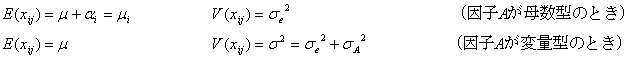
となります。ただし、因子の主効果は、
で定義されます。したがって、変量型一元配置実験のデータ１個当たりの標準不確かさは
となります。標準不確かさを求める場合、分散分析の不偏分散によって求められる分散は期待値そのものであるやではなくそれらの推定値
や
であることに注意しなければなりません。
また、標本平均（全データの平均）
の標準不確かさは
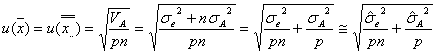
となります。
化学標準物質の不確かさを評価するときには、「枝分かれ実験分散分析」という分散分析の手法がよく用いられますが、その手法の詳細については本ホームページのアーカイブの項で解説してあります。ちなみに、上で紹介した一元配置実験の分散分析は「一段枝分かれ実験分析」に相当します。以下では、分散分析の応用例をあげておくことにします。
三段枝分かれ実験分散分析と経時変化に１次回帰を考慮したケース