|
�悤�����A���w�W�������̕s�m�����ւ̂����Ȃ� |
���m�点�i2002/05/14�`2009/03/06�j
2002/05/14 �悤�₭�s�m�����̃z�[���y�[�W�������ł��܂����B���ꂩ�班�����R���e���c���[�����Ă䂫�����Ǝv���Ă��܂��B
2002/05/16 �A�[�J�C�u�ɂ͎}����������̕��U���͂ɂ��s�m���������߂�Excel�}�N���t�@�C�����ڂ��܂����B
2002/12/04�@���v�w�̎Q�l���ɂ���ẮA�W�{���U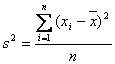 �ƕs�Ε��U
�ƕs�Ε��U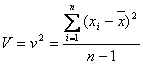 ����ʂ���Ȃ��Ŏg�p����Ă��č�������ꍇ�������̂ŁA���̃z�[���y�[�W�ł͗��҂��ł��邾����ʂ��ċL�q���邱�Ƃɂ��܂����B�܂��A��W�c�̕ꐔ�i����
����ʂ���Ȃ��Ŏg�p����Ă��č�������ꍇ�������̂ŁA���̃z�[���y�[�W�ł͗��҂��ł��邾����ʂ��ċL�q���邱�Ƃɂ��܂����B�܂��A��W�c�̕ꐔ�i����![]() �Ƃ���j�ɂ��Ă��A�^�̕ꐔ�͋L��
�Ƃ���j�ɂ��Ă��A�^�̕ꐔ�͋L��![]() �ŕ\���A���̐���l�̓n�b�g�O��t�����L��
�ŕ\���A���̐���l�̓n�b�g�O��t�����L��![]() �ŕ\���悤�ɂ��܂����B����ɁA�m���ϐ��͉p�啶���i���Ƃ���
�ŕ\���悤�ɂ��܂����B����ɁA�m���ϐ��͉p�啶���i���Ƃ���![]() �j�ŕ\���A���̎����l�i�m���ϐ�
�j�ŕ\���A���̎����l�i�m���ϐ�![]() ���\���鐔�l�ɑ�������ϐ��j�͉p������
���\���鐔�l�ɑ�������ϐ��j�͉p������![]() �ŕ\���̂���ʓI�ł����A�{�z�[���y�[�W�ł͓��ɒf��Ȃ�����A�m���ϐ��������l�����ɓ����p������
�ŕ\���̂���ʓI�ł����A�{�z�[���y�[�W�ł͓��ɒf��Ȃ�����A�m���ϐ��������l�����ɓ����p������![]() �ŋL�q���Ă��܂��B
�ŋL�q���Ă��܂��B
2003/02/27 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���u�}������������U���́v�̈�ʓI�ȕ��U���́iWindows,Mac�Ƃ��ɉғ��j�}�N����V.8.0����V.8.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�͕�܌W��k�Ƃ��Ďg�p����X�`���[�f���g��t�l��L�����R�x���狁�߂���悤�ɂ����_�ƌv�Z���ʕ\����̎�̕ύX�ł��B
2003/02/28 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���u�}������������U���́v�̈�ʓI�ȕ��U���́iWindows,Mac�Ƃ��ɉғ��j�}�N����V.8.1����V.8.2�Ƀo�[�W�����A�b�v���܂����B�ύX�_�͗L�����R�x�̃o�O�t�B�b�N�X�ł��B
2003/03/01 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���u�}������������U���́v�̈�ʓI�ȕ��U���́iWindows,Mac�Ƃ��ɉғ��j�}�N����V.8.2����V.8.3�Ƀo�[�W�����A�b�v���܂����B�ύX�_�͌v�Z���ʕ\������葽�l�Ō��₷�����A���[�U�[�̕X��}�����_�ł��B
2003/03/04 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���u�}������������U���́v�̈�ʓI�ȕ��U���́iWindows,Mac�Ƃ��ɉғ��j�}�N����V.8.3����V.8.4�Ƀo�[�W�����A�b�v���܂����B�ύX�_�͗L�����R�x�̃o�O�t�B�b�N�X�ƁA��͂Ɏg�p�����p�����[�^�̕\���@�\��lj������_�ł��B
2003/03/12 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���u�}������������U���́v�̈�ʓI�ȕ��U���́iWindows,Mac�Ƃ��ɉғ��j�}�N����V.8.4����V.8.5�Ƀo�[�W�����A�b�v���܂����B�ύX�_�͉�͌��ʂ̕\������茩�₷���A�]���ȋ@�\���Ȃ��V���v���ɂ������Ƃł��B
2003/03/27 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���u�}������������U���́v�̈�ʓI�ȕ��U���́iWindows,Mac�Ƃ��ɉғ��j�}�N����V.8.5����V.8.51�Ƀo�[�W�����A�b�v���܂����B��ȕύX�_�͗L�����R�x�̎Z�o���@�̌������Ə����ȃo�O�t�B�b�N�X�ł��B
2003/04/04 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���u�J��Ԃ��̂����A���̓}�N���v��V.2.7����V.2.71�Ƀo�[�W�����A�b�v���܂����B�}�N��v2.71�͌J��Ԃ��̂Ȃ��i![]() �j��A���͂��G���[�\�����邱�ƂȂ������ł���v���O�����ł��B
�j��A���͂��G���[�\�����邱�ƂȂ������ł���v���O�����ł��B
2003/04/05 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�f�ڂ��Ă���JCSS�Ή��u�J��Ԃ��̂����A���̓}�N���vV.2.71����ʓI�ȉ�A���͂ɂ����p�ł���}�N��V2.8��V���ɗp�ӂ��܂����B
2003/04/05 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɎO�i�}�����������A����V1.0���A�b�v���܂����B
2003/04/10 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̎O�i�}�����������A����V1.0��V1.1�Ƀo�[�W�����A�b�v���܂����B
2003/04/13 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̎O�i�}�����������A����V1.1��V1.2�Ƀo�[�W�����A�b�v���܂����B
2003/04/18 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̎O�i�}�����������A����V1.2��V1.3�Ƀo�[�W�����A�b�v���܂����B
2003/04/20 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɉ�A����0�}�N�� V.1.0 �i���_��ʂ��A�������͎����v�Z�V�X�e���j����щ�A����00�}�N�� V.1.0 �i���W�ϊ��������_��ʂ��A�������͎����v�Z�V�X�e���j���A�b�v���܂����B
2003/04/18 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̎O�i�}�����������A����V1.3��V1.4�Ƀo�[�W�����A�b�v���܂����B�o���ω����q�ɂ����萫�̕s�m�����͕��A�����W����![]() �̐���l
�̐���l![]() ���Ȃ킿�X��
���Ȃ킿�X��![]() �݂̂��l�������ꍇ�Ƃ��̕W���덷
�݂̂��l�������ꍇ�Ƃ��̕W���덷![]() �����l���������̂̂Q�̏ꍇ�ɂ��ĎZ�o���Ă���܂��B�Ȃ��A������A�����ł���c�����U�i
�����l���������̂̂Q�̏ꍇ�ɂ��ĎZ�o���Ă���܂��B�Ȃ��A������A�����ł���c�����U�i![]() �j�ȊO�̂��̑��́i��A�ɂ��Ȃ��j�덷���U�i
�j�ȊO�̂��̑��́i��A�ɂ��Ȃ��j�덷���U�i![]() �j�ɂ��Ă̓v�[�����Ȃ��ŎO�i�}������������U���͂��瓾���镪�U�����i
�j�ɂ��Ă̓v�[�����Ȃ��ŎO�i�}������������U���͂��瓾���镪�U�����i![]() �j�̒P���a���Ȃ킿
�j�̒P���a���Ȃ킿
![]()
�Ƃ��ĎZ�o���܂����B�덷���U�i![]() �j���������������ꍇ�ɂ́A�����ϓ����q�̕������a���v�[�����Ď��R�x�Ŋ������덷���U�i
�j���������������ꍇ�ɂ́A�����ϓ����q�̕������a���v�[�����Ď��R�x�Ŋ������덷���U�i![]() �j���덷���U�i
�j���덷���U�i![]() �j�̒l�Ƃ��ėp���ĉ������B
�j�̒l�Ƃ��ėp���ĉ������B
2003/04/23 �A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̎O�i�}�����������A����V1.4��V1.5�Ƀo�[�W�����A�b�v���܂����B�o���ω����q�ɂ����萫�̕s�m�����͕��A�����W����![]() �̐���l
�̐���l![]() ���Ȃ킿�X��
���Ȃ킿�X��![]() �Ƃ��̕W���덷
�Ƃ��̕W���덷![]() ���l���������̂����ɓ��ꂵ�܂����B
���l���������̂����ɓ��ꂵ�܂����B
2003/04/26�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̎O�i�}�����������A����V1.5��V1.6�Ƀo�[�W�����A�b�v���܂����B�o���ω����q�ɂ����萫�̕s�m�����Ƃ��ĉ�A�����̗\���l���狁�߂��M����Ԃ���l���z�Ɖ��肵�ĎZ�o�����W���s�m�����������\������悤�ɂ��܂����B
2003/04/28�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̎O�i�}�����������A����V1.6��V1.7�Ƀo�[�W�����A�b�v���܂����B�W���t�̕\���l�̕s�m�����̒�`��ύX���܂����B
2003/05/17�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɏd�ݕt��Deming��A����wd�}�N��V1.0���A�b�v���܂����B�Ɨ��ϐ�![]() ����я]���ϐ�
����я]���ϐ�![]() �̂�����ɂ����قȂ�s�m�����������Ă����`��A���͂��ł���}�N���ł��B
�̂�����ɂ����قȂ�s�m�����������Ă����`��A���͂��ł���}�N���ł��B
2003/05/22�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɏd�ݕt��Deming��A����wd�}�N��V1.0��V1.1�Ƀo�[�W�����A�b�v���܂����B
2003/05/25�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɏd�ݕt��Deming��A����wd�}�N��V2.0���A�b�v���܂����B���̃}�N���̓T�u���[�`�������������邱�Ƃɂ����![]() �̂悤�Ȑ��`�݂̂Ȃ炸����`��A�Ȑ�
�̂悤�Ȑ��`�݂̂Ȃ炸����`��A�Ȑ�![]() �ɂ��Ή��\�ȃ}�N���ł��B�������A���Ă͂߉\�ȃp�����[�^�̐�
�ɂ��Ή��\�ȃ}�N���ł��B�������A���Ă͂߉\�ȃp�����[�^�̐�![]() �͕W�{�f�[�^�i
�͕W�{�f�[�^�i![]() �j�̑���
�j�̑���![]() �ȓ��ł��B�܂��A�w������ΐ��`�ɕϊ��������̂����̑������ŕ\�����Ƃ��ł���A�T�u���[�`��
�ȓ��ł��B�܂��A�w������ΐ��`�ɕϊ��������̂����̑������ŕ\�����Ƃ��ł���A�T�u���[�`��![]() �i�ϑ���������\������T�u���[�`���j���ɓK�ȕϊ��v���O���������������邱�Ƃɂ��A���̃}�N���͎w������ΐ����̉�A���͂ɂ��Ή��ł��鉞�p�͈͂̍L���}�N���ł��B
�i�ϑ���������\������T�u���[�`���j���ɓK�ȕϊ��v���O���������������邱�Ƃɂ��A���̃}�N���͎w������ΐ����̉�A���͂ɂ��Ή��ł��鉞�p�͈͂̍L���}�N���ł��B
2003/05/27�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɏd�ݕt��������Deming��A����wdp2�}�N��V1.0���A�b�v���܂����B���̃}�N���Q����![]() �̉�A���͂��s���}�N���ł��B
�̉�A���͂��s���}�N���ł��B
2003/05/27�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɏd�ݕt��������Deming��A����wdp3�}�N��V1.0���A�b�v���܂����B���̃}�N���R����![]() �̉�A���͂��s���}�N���ł��B
�̉�A���͂��s���}�N���ł��B
2003/05/27�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɏd�ݕt��������Deming��A����wda1�}�N��V1.0���d�ݕt��������Deming��A���͂̉��p��P�Ƃ��ăA�b�v���܂����B���̃}�N��log-log��![]() �̉�A���͂��s���}�N���ł��B����log-log���͓��S�x�i
�̉�A���͂��s���}�N���ł��B����log-log���͓��S�x�i![]() �j�Ɖ��x�i
�j�Ɖ��x�i![]() �j�̊W��
�j�̊W��
�@�@�@�@�@![]()
�ɂ����āA![]() �ƒu�����������ł��B
�ƒu�����������ł��B
2003/06/21�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̏d�ݕt��Deming��A����wd�}�N��V2.0���o�[�W����v2.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A���l�����w�@�H�w�����@�̍������M�����̂��w�E�ɂ��ADeming��A���͂̌W���s��̋ߎ��v�Z�ɂ����Ċϑ�������![]() �̕Δ���
�̕Δ���![]() ��
��![]() �̒l�Ƃ��čŏ��̋ߎ��ł͊ϑ��l
�̒l�Ƃ��čŏ��̋ߎ��ł͊ϑ��l![]() ��p���܂����A�Q��ڈȍ~�̋ߎ��v�Z�ł͊ϑ��l
��p���܂����A�Q��ڈȍ~�̋ߎ��v�Z�ł͊ϑ��l![]() �����
�����![]() �����������ē����鐄��l�i�Ŋm�l�j
�����������ē����鐄��l�i�Ŋm�l�j
�@�@�@�@�@![]()
��������������s��v�Z�����A�W���Ɖ�A�W���̕s�m���������߂�悤�ɂ������Ƃł��B�ʏ�ϑ�������![]() �̕Δ���
�̕Δ���![]() ��
��![]() �̒l�Ƃ��Ă͊ϑ��l
�̒l�Ƃ��Ă͊ϑ��l![]() �����̂܂ܒ����ߎ��v�Z�ő�����ĉ�A�W���Ɖ�A�W���̕s�m���������߂Ă���Ⴊ�����̂ł����A���̂悤�ɂ���ƁA�������Ƃɕs�m�������ς��Ȃ��悤�ȓ���ȏꍇ�ɂ́A�ʏ�̂P������A���͂Ɠ������ʁA���킿�A
�����̂܂ܒ����ߎ��v�Z�ő�����ĉ�A�W���Ɖ�A�W���̕s�m���������߂Ă���Ⴊ�����̂ł����A���̂悤�ɂ���ƁA�������Ƃɕs�m�������ς��Ȃ��悤�ȓ���ȏꍇ�ɂ́A�ʏ�̂P������A���͂Ɠ������ʁA���킿�A![]() ���ɂ̂ݕs�m����������悤�Ȓʏ�̉�A���͂̏ꍇ�Ɠ����v�Z���ʂƂȂ��Ă��܂��܂��B�������A�������Ƃɕs�m�������ς��悤�ȏꍇ�ɂ́A�ϑ�������
���ɂ̂ݕs�m����������悤�Ȓʏ�̉�A���͂̏ꍇ�Ɠ����v�Z���ʂƂȂ��Ă��܂��܂��B�������A�������Ƃɕs�m�������ς��悤�ȏꍇ�ɂ́A�ϑ�������![]() �̕Δ���
�̕Δ���![]() ��
��![]() �̒l�Ƃ��āA�ϑ��l
�̒l�Ƃ��āA�ϑ��l![]() �����̂܂g���Ă��A���邢�͊ϑ��l
�����̂܂g���Ă��A���邢�͊ϑ��l![]() �����
�����![]() �����������ē����鐄��l
�����������ē����鐄��l![]() �𒀎�������Čv�Z���Ă��A���ʂɑ傫�ȍ��ق͐����Ȃ��A�ނ���O�҂̕���Deming�������悤�ɒ����ߎ��v�Z�̉��ʏ�P�C�Q��Ə��Ȃ��čςݑ����������闘�_�͂���܂��B
�𒀎�������Čv�Z���Ă��A���ʂɑ傫�ȍ��ق͐����Ȃ��A�ނ���O�҂̕���Deming�������悤�ɒ����ߎ��v�Z�̉��ʏ�P�C�Q��Ə��Ȃ��čςݑ����������闘�_�͂���܂��B
2003/07/21�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̏d�ݕt��Deming��A����wd�}�N��V2.1���o�[�W����v2.2�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����ы����U
����ы����U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂��A��A�W��
�{�ɂȂ��Ă����̂��A��A�W��![]() �̋ߎ��l
�̋ߎ��l![]() �Ƃ̕�
�Ƃ̕�![]() �ɂ��Ă̐��K�������i�ϑ���������
�ɂ��Ă̐��K�������i�ϑ���������![]() �j
�j
�@�@�@�@ �@
�̌W���s��
�@�@�@ �@�@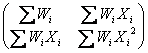
�̋t�s��
�@�@�@�@�@ 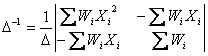
�̑Ίp�v�f����є�Ίp�v�f�ɑ�������悤�ɉ��߂��_�ł��B���Ȃ킿�A
�@�@�@�@�@ 
�̂悤�ɒ�`�������܂����B������
�@�@�@�@ �@
�͌W���s�̒l�ł��B�܂�����
![]()
�ŁA�d�݊�![]() ��
��

�ł��B�����ŁA![]() �͂��ꂼ��ϑ��_
�͂��ꂼ��ϑ��_![]() ��
��![]() ���W�̏d�݂ł���A
���W�̏d�݂ł���A![]() �͂������W�̕s�m������
�͂������W�̕s�m������![]() �͑Ή����镪�U�ł��B
�͑Ή����镪�U�ł��B
2003/07/23�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̏d�ݕt��Deming��A����wd�}�N��v2.2���o�[�W����v2.3�Ƀo�[�W�����A�b�v���܂����B���̐V�����o�[�W������Sheet4�ł́A�W�{�l�i![]() �j�Ƃ��̕s�m����
�j�Ƃ��̕s�m����![]() ���g���ďd�ݕt��Deming�@�ߎ��v�Z���狁�߂��P������A�����i�ϑ�������
���g���ďd�ݕt��Deming�@�ߎ��v�Z���狁�߂��P������A�����i�ϑ�������![]() ���瓾����Z���Ȑ����邢�͌��ʐ��Ƃ������A
���瓾����Z���Ȑ����邢�͌��ʐ��Ƃ������A![]() �ŕ\����܂��j��
�ŕ\����܂��j��![]() ��
��![]() ���t�ɂ��ē��������͋Ȑ�
���t�ɂ��ē��������͋Ȑ�![]() �ŕ\�����P��������ɂ��āA���m�����̓ǂݒl
�ŕ\�����P��������ɂ��āA���m�����̓ǂݒl![]() �Ƃ��̕s�m����
�Ƃ��̕s�m����![]() ���疢�m������
���疢�m������![]() �̒l�i�Z�x�j�Ƃ��̕s�m����
�̒l�i�Z�x�j�Ƃ��̕s�m����![]() ��\���ł���悤�ɂ��܂����B���̂悤�ɍZ���Ȑ�����ɂ��Ė��m�����̓ǂݒl����l�i�Z�x�j��\�����邱�Ƃ��u�t����v�ƌĂԂ��Ƃ�����܂��B
��\���ł���悤�ɂ��܂����B���̂悤�ɍZ���Ȑ�����ɂ��Ė��m�����̓ǂݒl����l�i�Z�x�j��\�����邱�Ƃ��u�t����v�ƌĂԂ��Ƃ�����܂��B
���̋t����̊��i���͊��j![]() ��
��
![]()
�ł���ƒ�`���܂��i�Q�l�����F ISO
6143:2001(E)�j�B��������ƁA���̎��Ɂu�덷�`�����v��K�p���āA�ǂݒl![]() �ɑΉ����関�m�����̗\���l
�ɑΉ����関�m�����̗\���l![]() �̕s�m����
�̕s�m����![]() �͈ȉ��̂悤�ɂ��ĎZ�o�ł��܂��B
�͈ȉ��̂悤�ɂ��ĎZ�o�ł��܂��B

���̎��ɓ��͂��ׂ���A�W��![]() �₻�̌덷���U����ы����U
�₻�̌덷���U����ы����U![]() �̒l�͏�q�̏d�ݕt��Deming�@�ߎ��v�Z�i�������ϑ��������͕��͊�
�̒l�͏�q�̏d�ݕt��Deming�@�ߎ��v�Z�i�������ϑ��������͕��͊�![]() ���瓾����
���瓾����![]() �Ƃ��܂��j�ŋ��߂��l���g���܂��B
�Ƃ��܂��j�ŋ��߂��l���g���܂��B
�������Ȃ���A���ۖ��Ƃ��ẮA�d�ݕt��Deming��A����wd�}�N��v2.3���킴�킴�V�����ϑ�������![]() �ɏ��������}�N���ɏ��������K�v�͂Ȃ��A�ϑ�������
�ɏ��������}�N���ɏ��������K�v�͂Ȃ��A�ϑ�������![]() �ɓ��͂��ׂ�Sheet1��
�ɓ��͂��ׂ�Sheet1��![]() ��
��![]() �̒l�����ւ��邾���ŁA���ꂩ�狁�߂���Sheet2�̉�A�W��
�̒l�����ւ��邾���ŁA���ꂩ�狁�߂���Sheet2�̉�A�W��![]() �̌덷���U
�̌덷���U![]() ����ы����U
����ы����U![]() �̒l�́A���̂܂�Sheet4�́u�t����v�Ɏg�p���ׂ�
�̒l�́A���̂܂�Sheet4�́u�t����v�Ɏg�p���ׂ�![]() ��
��![]() �̒l�Ƃ��Ďg�p���邱�Ƃ��ł��܂��B���̃}�N��v2.3��Sheet4�̋t����̌v�Z�}�N�������ۂ��̂悤�Ȏ�舵�������Ă��܂��B
�̒l�Ƃ��Ďg�p���邱�Ƃ��ł��܂��B���̃}�N��v2.3��Sheet4�̋t����̌v�Z�}�N�������ۂ��̂悤�Ȏ�舵�������Ă��܂��B
2003/07/26�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̏d�ݕt��Deming��A����wd�}�N��v2.3���o�[�W����v2.4�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A�o�[�W����v2.3��Sheet4�́u�t����v�̃}�N�����g���ɂ�Sheet�P�̊ϑ��l�ƕs�m�����̃f�[�^���͗���![]() ��
��![]() �̍��W�����ւ��ē��͂��Ȃ���Ȃ�Ȃ��Ƃ�������킵�����������̂��A���̃o�[�W�����ł͒ʏ�̃f�[�^���͂ł悢�悤�ɁASheet4�́u�t����v�}�N�������������܂����B
�̍��W�����ւ��ē��͂��Ȃ���Ȃ�Ȃ��Ƃ�������킵�����������̂��A���̃o�[�W�����ł͒ʏ�̃f�[�^���͂ł悢�悤�ɁASheet4�́u�t����v�}�N�������������܂����B
���Ȃ킿�ASheet1�Ŏg�p����d�ݕt��Deming�@�ߎ��v�Z���狁�߂��P������A�����i�ϑ�������![]() ���瓾����Z���Ȑ����邢�͌��ʐ��Ƃ������A
���瓾����Z���Ȑ����邢�͌��ʐ��Ƃ������A![]() �ŕ\����܂��j�̎������̂܂ܗp���āASheet4�́u�t����v�}�N���̊��i���͊��j
�ŕ\����܂��j�̎������̂܂ܗp���āASheet4�́u�t����v�}�N���̊��i���͊��j![]() ��
��
![]()
�ƒ�`���܂����B��������ƁA���̎��Ɂu�덷�`�����v��K�p���āA�ǂݒl![]() �ɑΉ����関�m�����̗\���l
�ɑΉ����関�m�����̗\���l![]() �̕s�m����
�̕s�m����![]() �͈ȉ��̂悤�ɂ��ĎZ�o�ł��܂��B
�͈ȉ��̂悤�ɂ��ĎZ�o�ł��܂��B

���������āA���̎��ɓ��͂��ׂ���A�W��![]() �₻�̌덷���U����ы����U
�₻�̌덷���U����ы����U![]() �̒l�͏�q�̏d�ݕt��Deming�@�ߎ��v�Z�i�ϑ�������
�̒l�͏�q�̏d�ݕt��Deming�@�ߎ��v�Z�i�ϑ�������![]() �j�ŋ��߂��l�����̂܂g�����Ƃ��ł��܂��B
�j�ŋ��߂��l�����̂܂g�����Ƃ��ł��܂��B
2003/07/27�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̏d�ݕt��Deming��A����wd�}�N��V1.1��V1.2�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����ы����U
����ы����U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂�������܂����B
�{�ɂȂ��Ă����̂�������܂����B
2003/08/22�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̉�A����wdp2�}�N�� v1.0 �i�d�ݕt��������Deming��A���͎����v�Z�V�X�e���j��V1.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����ы����U
����ы����U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂�������܂����B
�{�ɂȂ��Ă����̂�������܂����B
2003/08/22�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̉�A����wdp3�}�N�� v1.0 �i�d�ݕt��������Deming��A���͎����v�Z�V�X�e���j��V1.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����ы����U
����ы����U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂�������܂����B
�{�ɂȂ��Ă����̂�������܂����B
2003/08/23�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̉�A����wda1�}�N�� v1.0 �i�d�ݕt��������Deming��A���͎����v�Z�V�X�e���j��V1.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����ы����U
����ы����U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂�������܂����B
�{�ɂȂ��Ă����̂�������܂����B
2003/08/23�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̉�A����wda3�}�N�� v1.0 �i�d�ݕt��������Deming��A���͎����v�Z�V�X�e���j��V1.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����ы����U
����ы����U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂�������܂����B
�{�ɂȂ��Ă����̂�������܂����B
2003/08/23�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̏d�ݕt��Deming��A����wd0�}�N��
v1.0��V1.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂�������܂����B
�{�ɂȂ��Ă����̂�������܂����B
2003/08/23�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̏d�ݕt��Deming��A����wd0�}�N��
v2.0��V2.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A��A�W��![]() �̌덷���U
�̌덷���U![]() ����A�c���̕��U
����A�c���̕��U![]() �{�ɂȂ��Ă����̂�������܂����B
�{�ɂȂ��Ă����̂�������܂����B
2003/10/08�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�ɏd�ݕt���w������Deming��A����wda�}�N�� v1.0���A�b�v���܂����B
2004/01/13 ���낢��Ȋ��ɉ��p�\�Ȃ悤�Ƀ}�N���̕ύX�_������Deming�@�d�ݕt����A���̓G�N�Z��VBA�}�N�� �ix, y�����W�ɕs�m�����̂���ꍇ�̍ŏ����@�j ��O���t�쐬�G�N�Z��VBA�}�N���i�ߎ��Ȑ��`�揈���t���j �Ȃǂ̃G�N�Z��VBA�}�N�����A�b�v���܂����B
2004/01/17 �O�i�}�����������A���̓}�N���������Ł� v2.8���A�b�v���܂����B�P����A���̌��肪�����I�ɍs����悤�ɂ��܂����B
2004/01/30�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̓�i�}�����������A���̓}�N��v1.0��v1.1�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́AANOVA�\�̌덷�ϓ��̕s�Ε��U![]() �̊��Ғl��
�̊��Ғl��![]() �ɂȂ��Ă����̂�
�ɂȂ��Ă����̂�![]() �ɒ������܂����B�܂��A��A�ϓ��̕s�Ε��U
�ɒ������܂����B�܂��A��A�ϓ��̕s�Ε��U![]() �̊��Ғl��
�̊��Ғl��![]() �ƂȂ��Ă����̂�
�ƂȂ��Ă����̂�![]() �ɒ������܂����B�܂�����ɔ����A
�ɒ������܂����B�܂�����ɔ����A![]() �̊��Ғl
�̊��Ғl![]() ��
��![]() ����
����![]() �ɕς��܂����B���̑��A�\����̎�̕ύX�������܂����B
�ɕς��܂����B���̑��A�\����̎�̕ύX�������܂����B
2004/01/31�A�[�J�C�u�i���v�����\�t�g�j�̃y�[�W�̌J��Ԃ��̂����A���̓}�N��v2.81��v2.82�Ƀo�[�W�����A�b�v���܂����B�ύX�_�́A���萫�̕W���s�m������
![]() �ɂȂ��Ă����̂�
�ɂȂ��Ă����̂�![]() �ɒ������܂����B
�ɒ������܂����B
2004/02/14 ���v�����́u�����l�̂����i�}������������U���́`�����l�̂���Z�i�}������������U���́v�̇@���CT��
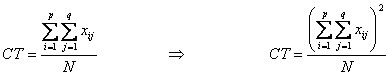
�̂悤�ɁA�\���~�X�̏C�����s���܂����B
2004/02/15 ���낢��Ȋ��ɉ��p�\�Ȃ悤�Ƀ}�N���̕ύX�_������Deming�@�d�ݕt����A���̓G�N�Z��VBA�}�N�� �ix, y�����W�ɕs�m�����̂���ꍇ�̍ŏ����@�j �̕s���i�p�����[�^���P�ϐ��̏ꍇ�A�W���s��̕Δ��������p�����[�^�ɑ��Ĕ���`�ɂȂ�悤�ȃ��f���ł͂��܂��ߎ��v�Z���ł��Ȃ����Ƃ�����j���C�����܂����B
2004/02/16�O���t�쐬�G�N�Z��VBA�}�N���i�ߎ��Ȑ��`�揈���t���j DrawGraph2.xls�̋@�\���A�b�v���āA�T�����܂ł̑�������������悤�ɂ��܂����i�]���͂R�����܂łł����j�B
2004/03/19 �O�i�}�����������A���̓}�N�����V�����Ł� v2.9���A�b�v���܂����B�o�͒l���܂Ƃ߂₷�����܂����B�܂��A�P����A���̌���̎�������Ƀo�O���������̂��܂����B
2004/03/25 �O�i�}�����������A���̓}�N�����V�����Ł� v2.9���������P�ɎO�i�}�����������A���̓}�N��v2.9�Ƃ��܂����B�܂��A����Ɠ����ɁA���V�����Ł� v2.9�ɂ����ĂP����A���̌���̎�������Ƀo�O���������̂��܂����B
2004/03/25 ��i�}�����������A���̓}�N��v1.3���A�b�v���܂����Bv1.2�ɂ����ĂP����A���̌���̎�������Ƀo�O���������̂��܂����B
2004/04/02 �J��Ԃ��̂����A���̓}�Nv2.83���A�b�v���܂����Bv2.82�ɂ����ĂP����A�̊��Ғl�Ƀo�O���������̂��܂����B
2008/03/06 �i�Ɓj�_�ѐ��Y������S�Z�p�Z���^�[�̈�Ɂ@�I��l���炲�w�E�������ӏ��ɂ��܂��ẮA���w�E�̒ʂ�̒ʂ�A
�u�Ɛ��w�I�ɂ͂Ȃ�܂����AF�l�̓��v�I����������j�����Ƃ�������ʂ͂Ȃ��Ƃ̌��_��95%�̐M�����i���Ȃ킿5%�̊댯���j�œ����Ă���̂ŁA���R��
���ɂ�镪�U�͂Ȃ��A���ׂċ��R�덷�ɂ�镪�U�Ƃ�������悢�ƍl�����܂��B�v�Ƃ������͕����ɂ��܂��ẮA���͂��炵�ē��R�A�O�҂́u���R�덷�v�́u�j
�����v�Ə����˂Ȃ�Ȃ������̂ŁA���̂悤�ɏC�����܂����B
2008/07/29�ܒi�}�����ꕪ�̓}�N�� v8.51��Excel2003�܂ł͐���ɓ����Ă����̂ł����AExcel2007��ł�
kfactor = Val(Worksheets("Sheet2").Range("G43"))
��kfactor�̂Ƃ���ŃG���[���o�Ă����̂ł����A���̌�����
Worksheets("Sheet2").Range("G42") = phieff
�̍s��phieff�̕\�����Ȃ����d���������Q�O�O�V�ł͐��l�╶���^�̒l�Ƃ��ĕ\������Ă��Ȃ��悤�ł��B
�����ł��̍s��
Worksheets("Sheet2").Range("G42") = val(phieff)
�̂悤��val�i�j�����g���Ă͂�����Ɛ��l�^�ł���Ɛ錾����悤�ɂ�����
����A�d���������Q�O�O�V�ł�����Ɂu��́v�}�N���������悤�ɂȂ�܂����B�����ŁA���̏C�����s�����}�N�����ܒi�}�����ꕪ�̓}�N�� v8.52�Ƃ��ăA�b�v���܂����B
2008/08/28�@�V�����Ȃ����s�m�����K�C�h ISO GUIDE 35:2006(E) 7.9 Insufficient repeatability of the measurement method���l���������U���́iWindows,Mac�Ƃ��ɉғ��j
��i�}�����ꕪ�̓}�N�� v9.2�Ɠ�i�}�����ꕪ�̓}�N�� v9.1���A�b�v���܂����B
�i�⑫�����j��f�́u��i�}�����ꕪ�̓}�N�� v9.1�v�ɂ����ẮA��i�ڂ̗v���ɂ��ϓ������̗v���ɔ�ׂĖ����ł���قǏ������ꍇ�́A�v�[�����O���s���āu��i�}�����ꕪ�́v���ł���悤�ɐV�����}�N���u��͂Q�v��t�����܂����B���ۂ̂����͒ʏ�ʂ�u�ɒi�}�����ꕪ�̓}�N��v9.1�v�́u��́v�{�^���������s���Čv�Z���ʂ������߂���A�uSPSS�v�{�^���������Ɠ�i�}�����ꕪ�́v�Ɏg�����f�[�^��Sheet3��SPSS�����̃f�[�^�Ƃ��ē\��t������̂ŁA����Sheet3�̃f�[�^�̒���B������������̂�Sheet7�ɂ܂��\��t���܂��B�����ŁASheet5���J���ϓ��v���Ɛ������Ȃǂ̕K�v���ڂ߂���A�u�c�[���v���u�}�N���v���u�f�[�^�Q�v�����s�����Sheet7��SPSS�����f�[�^��Sheet5�̃f�[�^�ʒu�ɕϊ�����ē\��t������̂ŁA�Ō�Ɂu�c�[���v���u�}�N���v���u��͂Q�v�����s����Ɠ�i�ڂ̗v���ɂ��ϓ��𑪒�덷�ϓ��Ƀv�[�����O�����f�[�^�ɂ��Ă̌v�Z���ʂ�Sheet6�ɕ\������܂��B
2008/10/17 �{�z�[���y�[�Windex.html���烊���N���Ă���y�[�Wdemingmethod.html�i�f�~���O�@�d�ݕt����A���̓v���O�������ꂱ��j�ɂ������̃v���O������V���ɉ������Y�y�[�W����V���܂����B
2009/03/03 �{�z�[���y�[�W��http://staff.aist.go.jp/s-shin/����http://staff.aist.go.jp/t.ihara/�Ɉ����z���܂����B
2009/03/03 �A�[�J�C�u�ɂ����A���͂̍��̂Ƃ���ɐV����ISO GUIDE 35:2006(E) 7.9 Insufficient repeatability of the
measurement method���l��������A���́iWindows��p�j�̍���݂��A�J��Ԃ��̂����A���̓}�N��v.3.6���ڂ��܂����B���̃v���O�����ł͉�A�������ɗL�Ӑ����Ȃ��Ƃ�������i![]() �j�̏ꍇ�ł��������萫�̕s�m���������߂���悤�ɂȂ��Ă��܂��B
�j�̏ꍇ�ł��������萫�̕s�m���������߂���悤�ɂȂ��Ă��܂��B
2009/03/06 �A�[�J�C�u�ɂ����A���͂̍��̃}�N���v���O�����J��Ԃ��̂����A���̓}�N��v.273�A�J��Ԃ��̂����A���̓}�N��v.282����т��J��Ԃ��̂����A���̓}�N��v.3.6�̌��ʕ\���̌㔼�̕����i�M����ԁj�̍��ڂ̕\�����ʂɈꕔ�o�O���������̂��C�����܂����B
2009/03/06 ���v�����́u���萫�ۏ؊��Ԃ̕ۏؒl�̕s�m�����v�̍���![]() �̓������������ɑ�����悤�����C�����Ă݂܂����B
�̓������������ɑ�����悤�����C�����Ă݂܂����B
|
�z�[�� | ���m�点 | �Q�l���� | �W�� | �Z�� | �g���[�T�r���e�B | ���U���� | ��A���� | ���v���� | �A�[�J�C�u | �����N |