|
ようこそ、化学標準物質の不確かさへのいざない |
回帰分析
x, y両座標ともに不確かさがある「重み付き回帰分析」(Deming法)については、本ホームページの「統計メモ」のページをご覧下さい。
直線回帰モデル
変数![]() と
と![]() からなる
からなる![]() 個の組
個の組![]() について散布図を描き、それら変数の間に何らかの関数関係
について散布図を描き、それら変数の間に何らかの関数関係![]() が想定される場合には、観測値
が想定される場合には、観測値![]() と関数曲線
と関数曲線![]() の距離が最小になるようにして、任意に選んだ多項式
の距離が最小になるようにして、任意に選んだ多項式
![]()
の係数![]() を決定することにより、推定関数
を決定することにより、推定関数![]() を見いだし、観測値
を見いだし、観測値![]() の誤差分散
の誤差分散![]() を見積もることが可能であり、これを(曲線)回帰分析と呼び、このようにして得られる推定関数のことを「
を見積もることが可能であり、これを(曲線)回帰分析と呼び、このようにして得られる推定関数のことを「![]() に対する
に対する![]() の回帰曲線」と呼んでいます。そして、回帰曲線の中でも最も単純でしかも実践的によく用いられるものは回帰直線(
の回帰曲線」と呼んでいます。そして、回帰曲線の中でも最も単純でしかも実践的によく用いられるものは回帰直線(![]() )で、そのようなモデルのことを「直線回帰モデル」と言います。
)で、そのようなモデルのことを「直線回帰モデル」と言います。
以下の直線回帰モデルでは、独立変数![]() には不確かさはなく(
には不確かさはなく(![]() )従属変数
)従属変数![]() にのみ不確かさがある(
にのみ不確かさがある(![]() )ものとします。また
)ものとします。また![]() の誤差の分布は正規分布をしており、その誤差分散
の誤差の分布は正規分布をしており、その誤差分散![]() は
は![]() の値によらず一定値
の値によらず一定値![]() をとるものと仮定します(
をとるものと仮定します(![]() )。このような仮定は通常成立している場合が多く、直線回帰モデルとして一般的なものです。
)。このような仮定は通常成立している場合が多く、直線回帰モデルとして一般的なものです。
そこで、いま任意の標本の組として
![]()
のような![]() 個の変数の組を考えることにします。ここで、
個の変数の組を考えることにします。ここで、![]() は独立変数(指定変数あるいは説明変数とも言う)、
は独立変数(指定変数あるいは説明変数とも言う)、![]() は従属変数(結果変数あるいは目的変数とも言う)であり、実現値
は従属変数(結果変数あるいは目的変数とも言う)であり、実現値![]() の確率変数
の確率変数![]() が
が
![]()
となるような直線の構造式(線形モデル)をもつものとします。![]() と
と![]() はこの構造式の形を決める構造パラメータ(母数)であり、
はこの構造式の形を決める構造パラメータ(母数)であり、![]() は確率変数ではない通常の変数です。また、
は確率変数ではない通常の変数です。また、![]() は正規分布
は正規分布![]() をする誤差の確率変数です。いま、確率変数
をする誤差の確率変数です。いま、確率変数![]() に実現値
に実現値![]() を代入すれば
を代入すれば
![]()
なる構造式が得られ、![]() は直線(母回帰直線)
は直線(母回帰直線)
![]()
すなわち
![]()
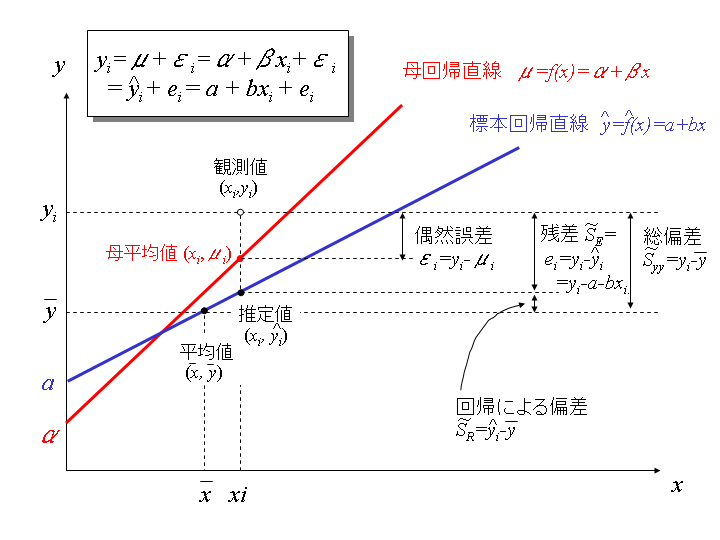
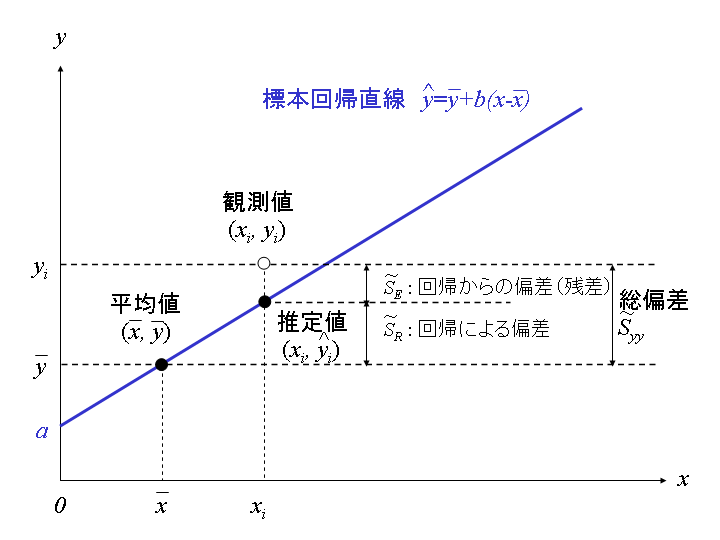
からの観測値のずれ(誤差)![]() に相当します。母回帰直線は、下図に見られるように、
に相当します。母回帰直線は、下図に見られるように、![]() に対応する無数の対象の
に対応する無数の対象の![]() の値の平均値である母平均
の値の平均値である母平均![]() の軌跡となります。すなわち
の軌跡となります。すなわち
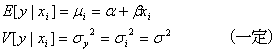
となるような期待値と分散をもつ母回帰直線ということです。
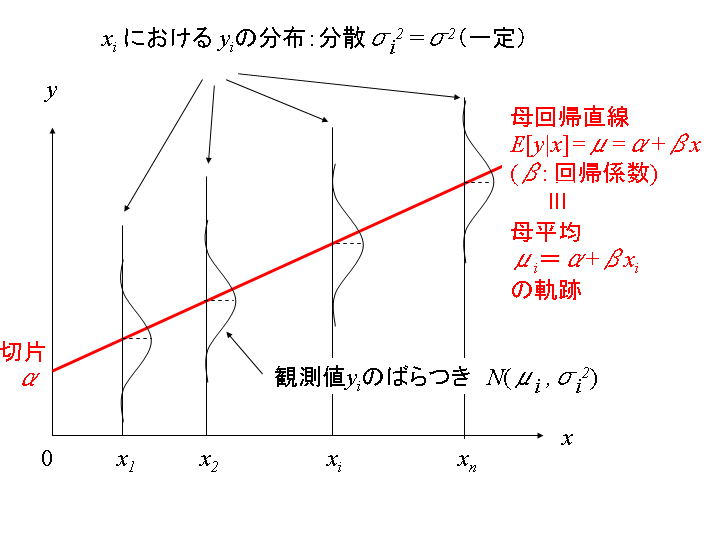
観測値![]() によって定義される標本回帰直線と母回帰直線
によって定義される標本回帰直線と母回帰直線
母回帰直線![]() の構造パラメータ(母数)である
の構造パラメータ(母数)である![]() (母切片)および
(母切片)および![]() (母回帰係数)の推定値
(母回帰係数)の推定値![]() と
と![]() を点推定するためには、上述の観測値
を点推定するためには、上述の観測値![]() と母平均
と母平均![]() との偏差
との偏差![]() の平方和
の平方和
![]()
を最小にするように、「Gaussの最小自乗法」を標本(標本回帰直線を![]() とすれば観測値は
とすれば観測値は![]() となります。ここで
となります。ここで![]() は観測値
は観測値![]() の推定値(真の値)です。)の偏差
の推定値(真の値)です。)の偏差![]() の平方和に適用して、
の平方和に適用して、
![]()
の極値条件
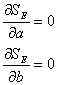
を求めることによって得られる連立方程式(正規方程式)

から、母数![]() と
と![]() の最良推定値である不偏推定値
の最良推定値である不偏推定値![]() と
と![]() が得られます。すなわち
が得られます。すなわち

となります。また
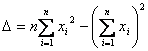
と定義すれば、母数![]() と
と![]() の推定値
の推定値![]() と
と![]() は
は
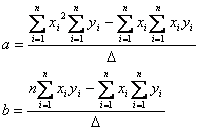
と書くこともできます。
したがって、推定された「![]() への
への![]() の回帰直線」(標本回帰直線)は、平均値
の回帰直線」(標本回帰直線)は、平均値![]() を通る切片
を通る切片![]() および傾き
および傾き![]() の直線
の直線
![]()
となります(下図参照。【注】この図および次図以下では、図中の大文字の![]() は、変動の偏差平方和
は、変動の偏差平方和![]() を表すのではなく偏差を表しています。したがって、たとえば、記号
を表すのではなく偏差を表しています。したがって、たとえば、記号![]() は本文中の誤差偏差
は本文中の誤差偏差![]() に相当することになります。)。ちなみに、正規方程式を求めるのに使った観測値
に相当することになります。)。ちなみに、正規方程式を求めるのに使った観測値![]() と回帰推定値
と回帰推定値![]() (回帰式
(回帰式![]() の
の![]() に
に![]() を代入して得られる推定値)との偏差
を代入して得られる推定値)との偏差![]()
![]()
のことを「残差」(あるいは単に「誤差」とも言います)と呼び、また![]() のことを「回帰からの変動の誤差変動」であり「残差平方和」(あるいは単に「誤差平方和」と呼ぶこともあります)と呼んでいます。残差
のことを「回帰からの変動の誤差変動」であり「残差平方和」(あるいは単に「誤差平方和」と呼ぶこともあります)と呼んでいます。残差![]() は
は
![]()
の関係式より
![]()
で表されるように、偶然誤差![]() と(母回帰直線と標本回帰直線との差)の和であることに注意する必要があります。
と(母回帰直線と標本回帰直線との差)の和であることに注意する必要があります。
観測値![]() は真の値
は真の値
残差平方和![]() は定義式
は定義式
![]()
の![]() に上で求めた
に上で求めた
![]()
を代入して、変形すれば

となります。ただし

および

です。一方、
![]()
であるから

となり、総変動![]() は「回帰による変動」
は「回帰による変動」![]() と「回帰からの変動」
と「回帰からの変動」![]() の和になります。
の和になります。
![]() の総変動
の総変動![]() に占める回帰平方和
に占める回帰平方和![]() の割合を「回帰の寄与率」と呼び
の割合を「回帰の寄与率」と呼び![]() で表します。すなわち
で表します。すなわち
![]()
あるいは
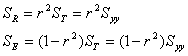
となります。したがって、![]() が
が![]() に近ければ
に近ければ![]() の変動の大部分が
の変動の大部分が![]() に対する回帰によって説明されることになり、
に対する回帰によって説明されることになり、![]() が
が![]() に近ければ
に近ければ![]() xの説明力はほとんどないことがわかります。この
xの説明力はほとんどないことがわかります。この![]() は
は![]() と
と![]() との「相関係数」に相当し、
との「相関係数」に相当し、![]() のことを「決定係数」と呼ぶことがあります。なお、相関係数
のことを「決定係数」と呼ぶことがあります。なお、相関係数![]() の符号は
の符号は![]() の符号と同じにします。
の符号と同じにします。
観測値![]() は真の値
は真の値![]() の周りに分布幅
の周りに分布幅![]() で正規分布していると仮定したので、偏差
で正規分布していると仮定したので、偏差![]() は中心値
は中心値![]() 、一定幅
、一定幅![]() で正規分布していることになります。したがって、
で正規分布していることになります。したがって、![]() の誤差、すなわち、測定値
の誤差、すなわち、測定値![]() の誤差
の誤差![]() 、すなわわち、「回帰推定の標準誤差」あるいは「残差標準偏差」
、すなわわち、「回帰推定の標準誤差」あるいは「残差標準偏差」![]() は
は
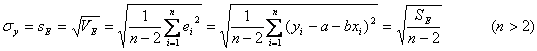
となります。分母が![]() ではなく
ではなく![]() になっているのは独立な変数
になっているのは独立な変数![]() の全個数
の全個数![]() から誤差
から誤差![]() を算出するのに
を算出するのに![]() と
と![]() と言う2つのパラメータ(
と言う2つのパラメータ(![]() に依存)を使っているので自由度が
に依存)を使っているので自由度が![]() に減少しているのです。したがって当然ながら、2点のみからなる変数系では回帰直線を推定できないことになります。
に減少しているのです。したがって当然ながら、2点のみからなる変数系では回帰直線を推定できないことになります。
母数![]() と
と![]() の最良推定値
の最良推定値![]() と
と![]() の誤差(標準偏差)は、それぞれ
の誤差(標準偏差)は、それぞれ

と定義されます。残差分散(誤差母分散)![]() は一定値であるから
は一定値であるから![]() の関数である
の関数である![]() も
も![]() の係数は
の係数は![]() のみの関数となっています。
のみの関数となっています。
また、母数![]() と
と![]() の不偏推定値である
の不偏推定値である![]() と
と![]() の期待値は、それぞれ
の期待値は、それぞれ
![]()
となります。さらに、![]() および
および![]() の期待値は、それぞれ
の期待値は、それぞれ
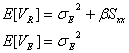
となります。ここで、![]() は残差分散(誤差母分散)
は残差分散(誤差母分散)![]() のことです。すなわち
のことです。すなわち
![]()
です。これら分散と期待値の証明は以下の通りです。
![]() は
は

と変形でき、![]() は互いに独立であり、
は互いに独立であり、![]() であるから
であるから
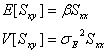
となります。これから
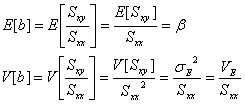
が得られます。
![]() は
は
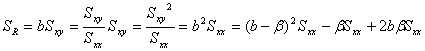
であるので
![]()
となります。一方、![]() は
は
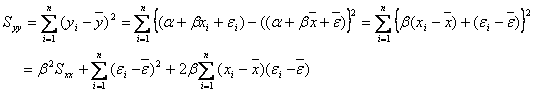
であるので
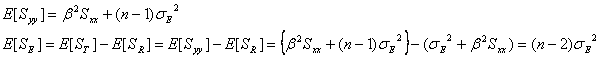
となります。したがって
![]()
となります。
観測値![]() (
(![]() )に繰り返しのない場合の回帰直線
)に繰り返しのない場合の回帰直線
残差分散(誤差母分散)![]() の正の平方根を回帰推定の標準誤差あるいは残差標準偏差と呼び
の正の平方根を回帰推定の標準誤差あるいは残差標準偏差と呼び![]() の記号を使って表します。これを回帰を用いないときの
の記号を使って表します。これを回帰を用いないときの![]() の標準偏差
の標準偏差![]() と比べると
と比べると
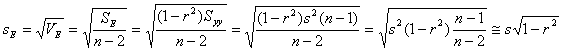
となるので、回帰で説明される部分を差し引くと、![]() の標準偏差はほぼ
の標準偏差はほぼ![]() 倍になります。つまり、相関がなければ
倍になります。つまり、相関がなければ![]() であるから
であるから![]() の残差標準偏差
の残差標準偏差![]() は回帰を用いないときの
は回帰を用いないときの![]() の標準偏差
の標準偏差![]() そのものになり、相関が強ければ
そのものになり、相関が強ければ![]() であるから、
であるから、![]() の残差標準偏差
の残差標準偏差![]() は限りなく
は限りなく![]() に近づき、すべての観測値
に近づき、すべての観測値![]() は標本回帰直線上の
は標本回帰直線上の![]() の推定値
の推定値![]() (真の値)に一致するようになることを意味しています。
(真の値)に一致するようになることを意味しています。
ここで、観測値![]() に繰り返しのない場合の回帰直線の分散分析表(ANOVA)を次に示します。
に繰り返しのない場合の回帰直線の分散分析表(ANOVA)を次に示します。
|
変動要因 |
偏差平方和 |
自由度 |
不偏分散 |
F値 |
不偏分散の期待値 |
|
回帰 |
|
|
|
|
|
|
残差 |
|
|
|
|
|
|
総変動 |
|
|
|
|
|
このANOVA表を用いることにより回帰性の有無を検定することができます。すなわち、
帰無仮説![]() (母回帰直線は回帰性をもたない)
(母回帰直線は回帰性をもたない)
対立仮説![]() (回帰性がある)
(回帰性がある)
とすれば、ANOVA表の各変動![]() は
は
![]() は自由度
は自由度![]() の
の![]() 分布
分布
![]() は自由度
は自由度![]() の
の![]() 分布
分布
![]() は自由度
は自由度![]() の
の![]() 分布
分布
となるので、帰無仮説![]() の下では
の下では
![]()
は自由度![]() の
の![]() 分布をすることになります。
分布をすることになります。
したがって、![]() ならば分子の
ならば分子の![]() の値は大きくなり、
の値は大きくなり、![]() の値も大きくなるので、この
の値も大きくなるので、この![]() の実現値
の実現値![]() を
を![]() 分布の右側棄却域と比較することにより回帰性の有無を検定することができます。
分布の右側棄却域と比較することにより回帰性の有無を検定することができます。
しかしながら、もし帰無仮説![]() (
(![]() は理論や過去の経験によって規定された仮説の値、通常は
は理論や過去の経験によって規定された仮説の値、通常は![]() )が
)が![]() の場合は
の場合は![]()
分布ではなく次のように![]() 分布で回帰性の有無を検定することになります。
分布で回帰性の有無を検定することになります。
これを対立仮説![]() に対して有意水準
に対して有意水準![]() (通常は
(通常は![]() )で検定するには
)で検定するには
![]()
が自由度![]() の
の![]() 分布をすることを考慮し、この
分布をすることを考慮し、この![]() の絶対値がスチューデントの
の絶対値がスチューデントの![]() 表の
表の![]() 点
点![]() より大きければ、帰無仮説
より大きければ、帰無仮説![]() を棄却し、推定回帰係数
を棄却し、推定回帰係数![]() は
は![]() とは有意差があると判断します。
とは有意差があると判断します。
推定母切片![]() は、そのもつ意味合いが実際的ではない場合が多いけれども、特殊な場合には帰無仮説
は、そのもつ意味合いが実際的ではない場合が多いけれども、特殊な場合には帰無仮説![]() (通常は
(通常は![]() 、すなわち、
、すなわち、![]() のとき
のとき![]() の母平均も
の母平均も![]() )を検定したい場合があり、このときは
)を検定したい場合があり、このときは
![]()
が自由度![]() の
の![]() 分布をすることを考慮して、推定回帰係数
分布をすることを考慮して、推定回帰係数![]() と同様に検定を行うことになります。
と同様に検定を行うことになります。
![]() という特殊な場合(通常はこの条件が満たされる)には、上述した
という特殊な場合(通常はこの条件が満たされる)には、上述した![]() 分布による検定と
分布による検定と![]() 分布による検定は一致します。すなわち、
分布による検定は一致します。すなわち、
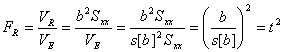
のような関係があり、どちらでも検定できることを意味しています。
![]()
観測値![]() (水準数:
(水準数:![]() ;繰り返し数:
;繰り返し数:![]() )に繰り返しがある場合の回帰直線
)に繰り返しがある場合の回帰直線
観測値![]() (水準数:
(水準数:![]() ;繰り返し数:
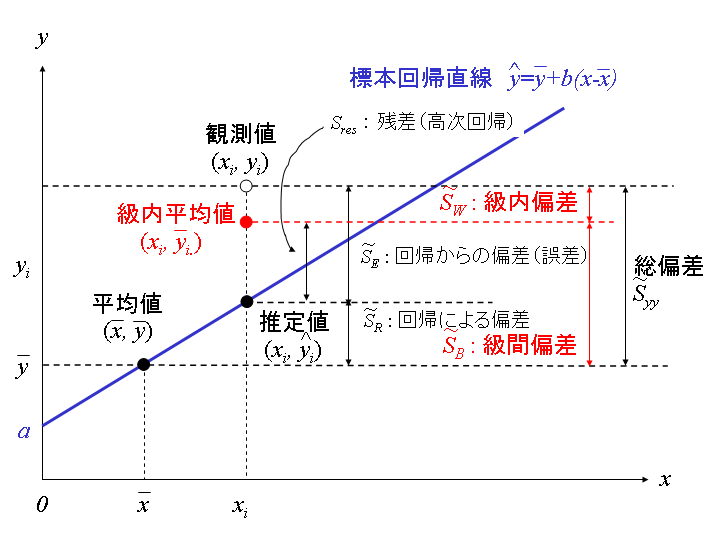
;繰り返し数:![]() )に繰り返しがある場合の回帰分析は上述の繰り返しのない回帰直線の場合より若干複雑になりますが、基本的な考え方は同じです。この場合は一元配置実験(一段枝分かれ実験)の分散分析に相当するので、総変動の偏差平方和(以降、大文字の
)に繰り返しがある場合の回帰分析は上述の繰り返しのない回帰直線の場合より若干複雑になりますが、基本的な考え方は同じです。この場合は一元配置実験(一段枝分かれ実験)の分散分析に相当するので、総変動の偏差平方和(以降、大文字の![]() は偏差平方和を意味する)
は偏差平方和を意味する)![]() は
は
![]()
のように級間変動成分![]() と級内変動成分
と級内変動成分![]() に分解することができます。級内変動
に分解することができます。級内変動![]() は独立変数
は独立変数![]() の
の![]() の値如何によって変化しない観測値
の値如何によって変化しない観測値![]() の純粋な誤差変動に相当するので、独立変数
の純粋な誤差変動に相当するので、独立変数![]() の
の![]() の値によって変化し得る変動成分は級間変動
の値によって変化し得る変動成分は級間変動![]() に相当します。そこで、級間変動
に相当します。そこで、級間変動![]() は回帰に関わる変動と見なすことができるので、これを1次回帰に相当する回帰による変動
は回帰に関わる変動と見なすことができるので、これを1次回帰に相当する回帰による変動![]() と残りの変動(高次回帰変動)
と残りの変動(高次回帰変動)![]() に分解することにします。すなわち
に分解することにします。すなわち
![]()
のうになります。この残りの変動(高次回帰変動)![]() は回帰残差(あるいは単に残差)の変動あるいは不適合度の変動とも呼ばれることがあり、回帰直線への当て嵌めの悪さ(直線からのふれ)、すなわち、回帰直線(1次回帰)の不適合度を見積もる目安となっています。その理由は、残りの変動(高次回帰変動)
は回帰残差(あるいは単に残差)の変動あるいは不適合度の変動とも呼ばれることがあり、回帰直線への当て嵌めの悪さ(直線からのふれ)、すなわち、回帰直線(1次回帰)の不適合度を見積もる目安となっています。その理由は、残りの変動(高次回帰変動)![]() と純粋な誤差変動に相当する級内変動
と純粋な誤差変動に相当する級内変動![]() をそれぞれの自由度で割って得られる不偏分散
をそれぞれの自由度で割って得られる不偏分散![]() と
と![]() の比を
の比を![]() と定義すれば
と定義すれば
![]()
は自由度![]() と
と![]() の
の![]() 分布に従い、これは帰無仮説
分布に従い、これは帰無仮説![]() :回帰は1次回帰
:回帰は1次回帰![]() ではないことを検定することになり、もし
ではないことを検定することになり、もし![]() の実現値
の実現値![]() が、自由度
が、自由度![]() と
と![]() の
の![]() 分布における
分布における![]() (通常
(通常![]() )の右側棄却域よりも大きければ、直線回帰への不適合度(当て嵌めの悪さ)が大きいと言うことになり、1次回帰よりさらに高次の回帰を考慮する必要があるという1次回帰の不適合性の指標になるからです。
)の右側棄却域よりも大きければ、直線回帰への不適合度(当て嵌めの悪さ)が大きいと言うことになり、1次回帰よりさらに高次の回帰を考慮する必要があるという1次回帰の不適合性の指標になるからです。
総変動![]() から回帰による変動
から回帰による変動![]() を差し引いたものは誤差変動
を差し引いたものは誤差変動![]() と呼ばれ
と呼ばれ
![]()
のように、それはまた回帰残差![]() と級内変動
と級内変動![]() の和となっており、この誤差変動
の和となっており、この誤差変動![]() は回帰からの変動とも呼ばれ、回帰直線の回帰性の度合い(帰無仮説
は回帰からの変動とも呼ばれ、回帰直線の回帰性の度合い(帰無仮説![]() すなわち回帰直線の回帰係数(直線の傾き)が
すなわち回帰直線の回帰係数(直線の傾き)が![]() である)を検定するのに用いられる。すなわち、回帰変動
である)を検定するのに用いられる。すなわち、回帰変動![]() による不偏分散
による不偏分散![]() と誤差変動
と誤差変動![]() による不偏分散
による不偏分散![]() との比
との比![]()
![]()
の実現値![]() が、自由度
が、自由度![]() と
と![]() の
の![]() 分布における
分布における![]() (通常
(通常![]() )の右側棄却域に入るかどうかを検定し、回帰性の有無(回帰直線の傾き
)の右側棄却域に入るかどうかを検定し、回帰性の有無(回帰直線の傾き![]() の有無)を判定するわけです。
の有無)を判定するわけです。
また、回帰そのものがこの観測系にあるのかどうかを検定するためには、級間変動![]() による不偏分散
による不偏分散![]() と級内変動
と級内変動![]() による不偏分散
による不偏分散![]() との比
との比![]()
![]()
の実現値![]() が、自由度
が、自由度![]() と
と![]() の
の![]() 分布における
分布における![]() (通常
(通常![]() )の右側棄却域に入るかどうかを検定することになります。この場合、帰無仮説
)の右側棄却域に入るかどうかを検定することになります。この場合、帰無仮説![]() すなわち
すなわち![]() であり、独立変数
であり、独立変数![]() の
の![]() の値の如何を問わず従属変数
の値の如何を問わず従属変数![]() の平均値
の平均値![]() が変化しないで一定値
が変化しないで一定値![]() をとることになり、結果として回帰成分がこの観測系では存在しないことを意味することになります。
をとることになり、結果として回帰成分がこの観測系では存在しないことを意味することになります。
観測値![]() (水準数:
(水準数:![]() ;繰り返し数:
;繰り返し数:![]() )に繰り返しがある場合の回帰直線の分散分析表(ANOVA)を次に示します。表中の
)に繰り返しがある場合の回帰直線の分散分析表(ANOVA)を次に示します。表中の![]() は全観測データ数で
は全観測データ数で
![]()
です。
|
変動要因 |
偏差平方和 |
自由度 |
不偏分散 |
F値 |
不偏分散の期待値 |
|
級間 |
|
|
|
|
|
|
回帰 |
|
|
|
|
|
|
残差 |
|
|
|
|
|
|
級内 |
|
|
|
|
|
|
誤差 |
|
|
|
|
|
|
総変動 |
|
|
|
|
|
(注)回帰による変動の偏差平方和は、また、![]() とも書けます。
とも書けます。
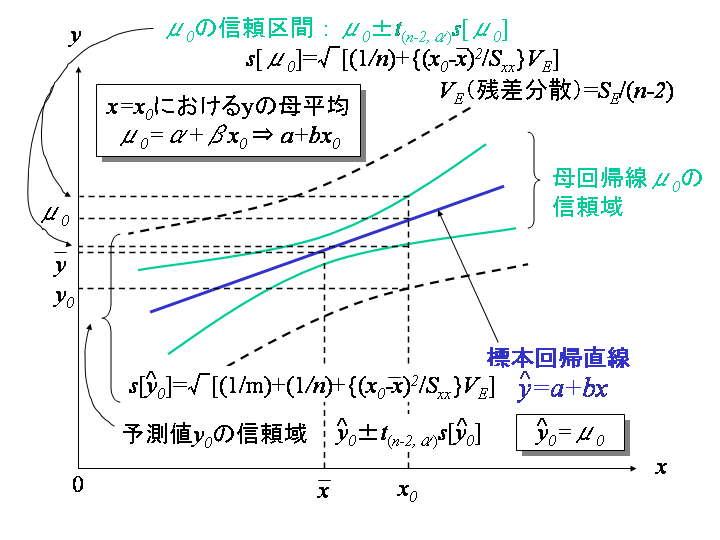
母回帰線![]() の信頼域と予測値
の信頼域と予測値![]() の信頼域
の信頼域
この項では繰り返しのない回帰直線についてのみ記述することにしますが、繰り返しのある場合にも応用可能です。上述の説明からも明らかなように、母回帰直線の母数である母切片![]() と母回帰係数
と母回帰係数![]() の
の![]() 信頼区間は
信頼区間は
![]()
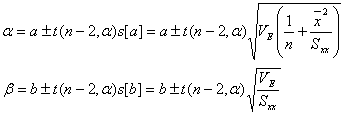
で与えられます。しかしながら回帰を用いる推定ではこのような回帰直線の母数そのものの推定よりも、独立変数![]() がある特定の値
がある特定の値![]() をとったときの従属変数
をとったときの従属変数![]() の母平均
の母平均![]() の推定の方がより重要である場合が多い。その推定値は
の推定の方がより重要である場合が多い。その推定値は
![]()
で与えられるのは自明であるが、この形では推定値![]() と
と![]() に相関があるので母平均の推定値
に相関があるので母平均の推定値![]() の標準誤差を求めることは容易ではありません。そこで上式を変形した
の標準誤差を求めることは容易ではありません。そこで上式を変形した
![]()
においては、確率変数![]() と
と![]() とは統計的に独立であるので、
とは統計的に独立であるので、
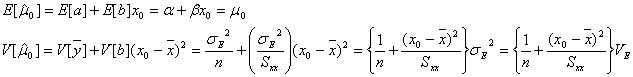
のように、母平均の推定値![]() の期待値と分散が得られるので、母平均の推定値
の期待値と分散が得られるので、母平均の推定値![]() の標準誤差
の標準誤差![]() は
は
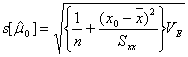
となります。したがって母平均![]() の
の![]() 信頼区間は
信頼区間は
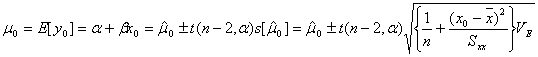
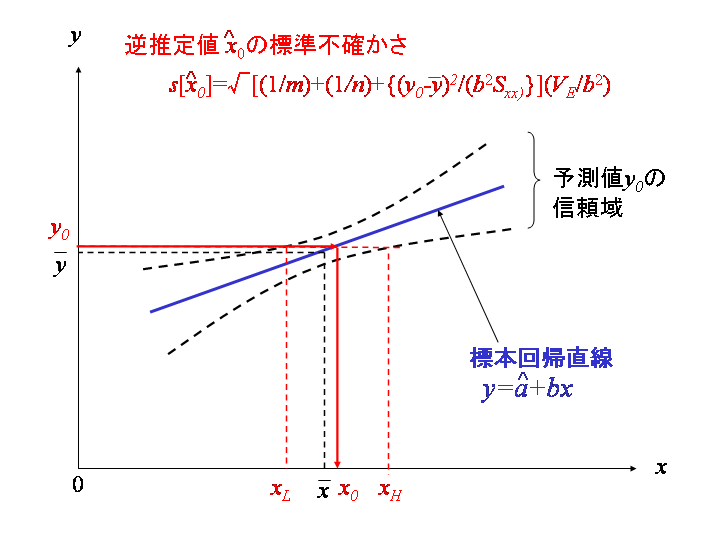
で与えられます。![]() の値を動かすと、
の値を動かすと、![]() で母平均の推定値
で母平均の推定値![]() の標準誤差
の標準誤差![]() は最小になり、
は最小になり、![]() が
が![]() より離れるに従って
より離れるに従って![]() は大きくなり、その信頼区間
は大きくなり、その信頼区間![]() は下図の緑色の実線のように双曲線的に広がって行きます。
は下図の緑色の実線のように双曲線的に広がって行きます。
ところで、母平均の推定値![]() の標準誤差(標準不確かさ)
の標準誤差(標準不確かさ)![]() の中身を吟味するために、その分散
の中身を吟味するために、その分散![]() の中身を考えてみると
の中身を考えてみると
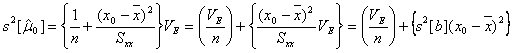
のように、![]() 個の観測値
個の観測値![]() の標準誤差(誤差分散
の標準誤差(誤差分散![]() の平均値である
の平均値である![]() )の項と回帰係数(回帰直線の傾き)
)の項と回帰係数(回帰直線の傾き)![]() にのみ関わる分散
にのみ関わる分散![]() の項の和となっていることがわかります。
の項の和となっていることがわかります。
ここまでの記述は標本の観測データのみに基づいて得られる母平均の推定値![]() の標準不確かさについて記述したものであるが、この標本系の回帰分析結果(残差分散
の標準不確かさについて記述したものであるが、この標本系の回帰分析結果(残差分散![]() や回帰係数の標準偏差
や回帰係数の標準偏差![]() の値)を使って、独立変数
の値)を使って、独立変数![]() が
が![]() において新しい実験や観測を行ったとき、従属変数
において新しい実験や観測を行ったとき、従属変数![]() の値
の値![]() がどのような範囲(予測値
がどのような範囲(予測値![]() の標準不確かさ
の標準不確かさ![]() で定義される
で定義される![]() 信頼区間)に入るのかを予測したい場合があります。このとき、他に情報がなければ予測値
信頼区間)に入るのかを予測したい場合があります。このとき、他に情報がなければ予測値![]() は、母平均の推測値
は、母平均の推測値![]() と同じであると見なさざるを得ませんから
と同じであると見なさざるを得ませんから
![]()
となります。そこで、新しい実験(観測)系における従属変数![]() の値(観測値)
の値(観測値)![]() と予測値(真の値)
と予測値(真の値)![]() との偏差の期待値と分散を求めてみることにします。すなわち
との偏差の期待値と分散を求めてみることにします。すなわち
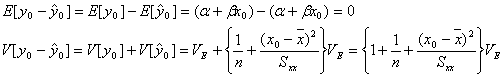
となりますから、新しい観測値![]() は新しい標準誤差(標準不確かさ)
は新しい標準誤差(標準不確かさ)![]()
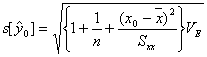
で規定される![]() 信頼区間(下図の黒色の波線で囲まれた範囲)
信頼区間(下図の黒色の波線で囲まれた範囲)
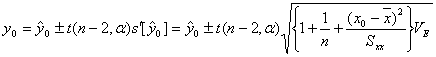
に入ることが予測されます。この範囲は標本の信頼区間より観測値1個分の標準誤差が付加された拡張不確かさで表現される信頼区間に相当します。
この証明は別の方法によっても可能です。すなわち、実際の![]() の値は
の値は
![]()
のように母平均![]() に誤差
に誤差![]() が1個分加わるので、
が1個分加わるので、![]() の実現値を
の実現値を![]() で予測した場合の予測誤差
で予測した場合の予測誤差![]() は
は
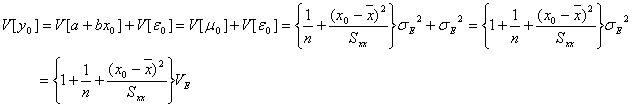
のように、誤差![]() による誤差分散
による誤差分散![]() の分だけ大きくなります。
の分だけ大きくなります。
また、新たな実験系(観測系)において観測値![]() 個分の平均値
個分の平均値![]() を求めた場合、その平均値についての信頼区間を知りたいことも現実にはあり得ます。このような場合は上記の観測値1個分の考察から類推して、その信頼区間は
を求めた場合、その平均値についての信頼区間を知りたいことも現実にはあり得ます。このような場合は上記の観測値1個分の考察から類推して、その信頼区間は
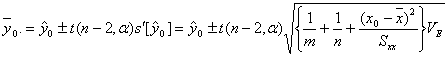
となり、上述の観測値1個分の信頼区間より若干狭くなります。
逆推定(検量線を使って![]() から
から![]() を推定する)
を推定する)
標本の組![]() から、上記のように、標本回帰直線
から、上記のように、標本回帰直線![]() を作成した後、その標本回帰直線を検量線として、従属変数
を作成した後、その標本回帰直線を検量線として、従属変数![]() から独立変数
から独立変数![]() を逆に推定したい場合があり、このような操作のことを「逆推定」と呼びます。逆推定を行った場合にどれくらいの不確かさで
を逆に推定したい場合があり、このような操作のことを「逆推定」と呼びます。逆推定を行った場合にどれくらいの不確かさで![]() を推定できるかは関心のあるところです。標本回帰式は
を推定できるかは関心のあるところです。標本回帰式は
![]()
と変形できるから、![]() に対する
に対する![]() の推測値
の推測値![]() は
は
![]()
となります。ここで、![]() は定数、
は定数、![]() と
と![]() は統計量であり、標本回帰線から見て
は統計量であり、標本回帰線から見て![]() は新しい観測値であるから、
は新しい観測値であるから、![]() は3つの正規分布する変数
は3つの正規分布する変数![]() の関数と見ることができます。したがって、
の関数と見ることができます。したがって、![]() は
は![]() の真の値を平均とする正規分布に近似することができ、その推定値
の真の値を平均とする正規分布に近似することができ、その推定値![]() の分散
の分散![]() は
は

となります。もし![]() が
が![]() 個の平均値
個の平均値![]() である場合には、上記分散は
である場合には、上記分散は
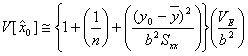
となります。したがって求める逆推定の標準誤差(標準不確かさ)は
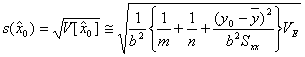
であり、![]() 信頼水準での信頼区間
信頼水準での信頼区間![]() は
は
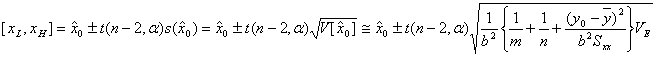
となります。
従属変数![]() にのみ重みの異なる不確かさがある(
にのみ重みの異なる不確かさがある(![]() )場合の回帰直線
)場合の回帰直線
従属変数![]() が
が![]() の母回帰直線上に乗ると予測でき、
の母回帰直線上に乗ると予測でき、![]() に相異なる不確かさ
に相異なる不確かさ![]() が含まれている場合には、重み
が含まれている場合には、重み![]() を
を
![]()
と定義することによって、回帰係数![]() の最良推定値(最確値)
の最良推定値(最確値)![]() および
および![]() を重み
を重み![]() を使って次のようにして求めることができます。
を使って次のようにして求めることができます。

また、![]() の推定の誤差分散は
の推定の誤差分散は

となります。もし測定値![]() の個々の不確かさについての分散
の個々の不確かさについての分散![]() がわかってはいないが、それぞれの繰り返し測定回数
がわかってはいないが、それぞれの繰り返し測定回数![]() がわかっている場合には、重み
がわかっている場合には、重み![]() を測定回数
を測定回数![]() で代表させてもよい。すなわち
で代表させてもよい。すなわち
![]()
として上述のパラメータを算出することもできます。
また、重み![]() が均等である(測定値
が均等である(測定値![]() の分散
の分散![]() がすべて等しく
がすべて等しく![]() )である場合には
)である場合には
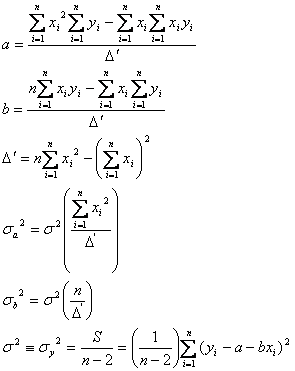
となり、一般的な1次式回帰直線のパラメータと一致するようになります。
独立変数![]() と従属変数
と従属変数![]() のいずれにも不確かさがある(
のいずれにも不確かさがある(![]() )場合の回帰直線(Taylorの方法)
)場合の回帰直線(Taylorの方法)
このような場合は、もし独立変数![]() の標準不確かさ(標準偏差)
の標準不確かさ(標準偏差)![]() が
が![]() の値によって変わらなければ、その不確かさをすべて従属変数
の値によって変わらなければ、その不確かさをすべて従属変数![]() の標準不確かさ(標準偏差)
の標準不確かさ(標準偏差)![]() に組み込んだ新しい標準不確かさ(標準偏差)
に組み込んだ新しい標準不確かさ(標準偏差)![]()
![]()
を![]() すなわち
すなわち![]() あるいは
あるいは![]() と定義し直すことにより、上述の(通常の)回帰直線分析に置き換えることができます。
と定義し直すことにより、上述の(通常の)回帰直線分析に置き換えることができます。
独立変数と従属変数のどちらにも誤差がある場合の重み付き直線回帰分析(Demingの簡略法)
確率変数である独立変数![]() と従属変数
と従属変数![]() の組
の組![]() が
が
![]()
のような1次式の直線関係にあり、これに対応する観測値(測定値)が
![]()
のように、それぞれ![]() および
および![]() の測定誤差をもっているものとします。また、
の測定誤差をもっているものとします。また、![]() および
および![]() をそれぞれ誤差
をそれぞれ誤差![]() および
および![]() の標準偏差とします。
の標準偏差とします。
さて、問題はどのようにして回帰直線の母数![]() と
と![]() の推定を行い、また
の推定を行い、また![]() および
および![]() の推定値を求めるかと言うことが課題ですが、
の推定値を求めるかと言うことが課題ですが、![]() と
と![]() に対応する「重み」がわかれば通常の最小二乗法によってそれらの推定値を求めることができます。
に対応する「重み」がわかれば通常の最小二乗法によってそれらの推定値を求めることができます。
そこで、誤差![]() および
および![]() の不偏分散をそれぞれ
の不偏分散をそれぞれ![]() および
および![]() とし、その比が
とし、その比が![]() であるとすると
であるとすると
![]()
のようになります。すなわち、![]() と
と![]() はそれぞれ不偏分散
はそれぞれ不偏分散![]() および
および![]() に比例する量ですが、これらの逆数である
に比例する量ですが、これらの逆数である![]() と
と![]() 、あるいはそれらの定数倍である
、あるいはそれらの定数倍である![]() と
と![]() はそれぞれ誤差
はそれぞれ誤差![]() および
および![]() の「重み」に相当します。
の「重み」に相当します。
いま、独立変数![]() と従属変数
と従属変数![]() の推定値をそれぞれ
の推定値をそれぞれ![]() および
および![]() とし、条件
とし、条件
![]()
の下で「重み付き平方和」を![]() とすれば
とすれば
![]()
を最小にして推定値を求めるのがDemingの方法です。上述の2つの式から
![]()
が得られますが、![]() と
と![]() およびすべての
およびすべての![]() に関してこの量
に関してこの量![]() を最小になるようにします。
を最小になるようにします。
ここで、観測値![]() および
および![]() の平均値をそれぞれ
の平均値をそれぞれ![]() および
および![]() とし、次のような量
とし、次のような量![]()

を導入すれば
![]() は次のような正規方程式
は次のような正規方程式
![]()
の解
![]()
として得られます。
また、![]() は
は
![]()
から求められ、推定値![]() および
および![]() は次のようにして求めることができます。すなわち
は次のようにして求めることができます。すなわち
![]()
とすれば
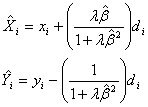
となります。最後に不偏分散![]() および
および![]() の推定値は
の推定値は

のようにして求めることができます。![]() は上述の式
は上述の式
![]()
から求められますが、
![]()
という式からも直接求めることができます。
この量![]() は
は
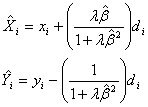
の式から推定値![]() および
および![]() を算出したときの
を算出したときの![]() の最小値に等しく、また
の最小値に等しく、また
![]()
なる量は自由度![]() のある種の分散、すなわち、一般的な回帰直線の誤差分散
のある種の分散、すなわち、一般的な回帰直線の誤差分散![]() の推定値と見ることもできます。
の推定値と見ることもできます。
原点を通る回帰直線
従属変数![]() が原点を通る母回帰直線
が原点を通る母回帰直線![]() 上に乗ると仮定でき、独立変数
上に乗ると仮定でき、独立変数![]() には誤差がなく、また、測定値
には誤差がなく、また、測定値![]() の誤差がすべて同じである場合には、母数である回帰係数(傾き)
の誤差がすべて同じである場合には、母数である回帰係数(傾き)![]() の最良推定値(最確値)
の最良推定値(最確値)![]() とその分散は
とその分散は

となります。