三段枝分かれ実験の構造モデル（質量比混合法による特定標準液の調製に係わる不確かさを求める）

　        《一段目（経時変化因子）を直線回帰（１次式）で近似するケース》

 

　特定標準液の保存安定保証期間（６ヶ月）内における各標準液の表示値とその不確かさならびにその特定標準液を使って校正機関が特定二次標準液を校正（jcss校正）するときの不確かさの見積もりに関する統計処理の考え方を以下にまとめておきます。

 

　まず特定標準液については、０，２，４，６ヶ月目に質量比混合法で目標濃度の標準液を３ロットずつ調製し、また各ロットからそれぞれ２本ずつのアンプルに標準液を小分けし、校正保証期間（６ヶ月）内の任意の期間一定の条件に保って保存することにします。次いで、このように一定期間（０，２，４，６ヶ月）保存しておいた各アンプル（被検溶液）につき、６ヶ月目に濃度既知（質量比混合法で得られた値を濃度の表示値とする）の標準液１ロットを別途調製し、この濃度を標準として２回の繰り返し測定（たとえばGC分析）により被検溶液の濃度測定を行います。したがって、これら被検溶液の濃度に関する標本データは４（日間変動の水準数）×３（調製ロット間変動の水準数）×２（アンプル間変動の水準数）×２（繰り返し測定回数）の大きさになり、その構造モデルは

 

 

となります。

 

このような実験モデルは対応のない変量模型である「三段枝分かれ実験モデル」となり、そのANOVA表は次のようになります。

 

要因

平方和

自由度

分散

期待値

経時変化

ロット誤差

アンプル

測定誤差

 

したがって、特定標準液の合成標準不確かさ ucと拡張不確かさUは以下のようになります。

 

                           

        　(ここで、通常は包含係数とする)

 

ただし、被検溶液（特定標準液）の測定濃度は、たとえば呼称濃度が1,000 ppmの場合には、規格化のために

 

              測定濃度＝検量線用標準液の質量比混合法による調製濃度

                            ×（被検溶液のガスクロ分析ピーク面積／検量線用標準液の

                            ガスクロ分析ピーク面積）×（1,000／被検溶液の調製濃度）

 

として算出します。

 

経時変化が一次回帰直線に乗ると仮定したとき

 

上述の三段枝分かれ実験の構造モデル

 

 

を、母平均μおよび経時変化とその他の変動要因の項からなるように書き改めます。

 

                           

 

                   ここで、：経時変化（）

：その他の変動（）

 

１次式回帰の偏差平方和は

 

 

と定義する。ただし、は時間変動に対する偏差平方和

 

                           

 

である。

 

ちなみに、このような３段枝分かれ実験回帰分析のANOVA表は

 

 

変動要因

偏差

平方

和

自由度

不偏

分散

不偏分散の期待値

級間変動（）

１次回帰

高次回帰（残差）

級内変動（）

ロット

アンプル

測定誤差

 

級内変動

 

回帰残差

 

のように表すことができます。ただし、総変動の偏差平方和を

 

             

 

と定義すれば、

 

 

です。

 

 

の部分の分解を行って直線回帰モデルを適用すると

 

+

 

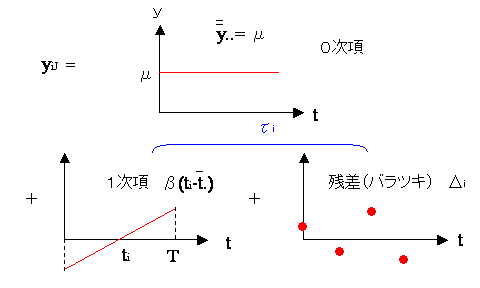
すなわち、

 

 

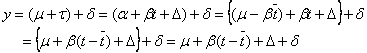
となります。

 

したがって、直線回帰の構造モデルから得られる確率変数の不確かさの分散は

 

 

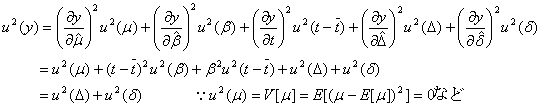
となります。これは、また測定値が回帰直線による推定値からの偏差分散と見ることもできます。すなわち、

 

                           

 

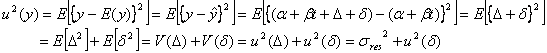
ところで、私たちが目標値としているのは質量比混合法で調製した標準液の濃度（表示値）ですから、不確かさの分散は

 

                           

 

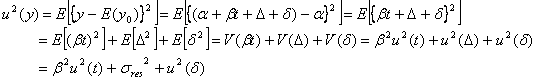
となります。ここで、通常は時間は一定値での不確かさはないので、上式右辺の第１項は消え、結局

 

                           

 

となってしまうわけですが、私たちの場合には、この表示値を基準にしての期間の間の推定値の不確かさを定義しようとするわけですから、にはの不確かさがあり、その不確かさは保証期間の間の時間平均と考えれば

 

                           

 

 

となります。

 

よって、表示値の合成標準不確かさは次式の合成分散から算出できます。

 

 

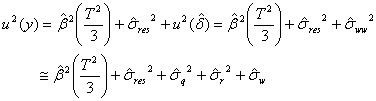
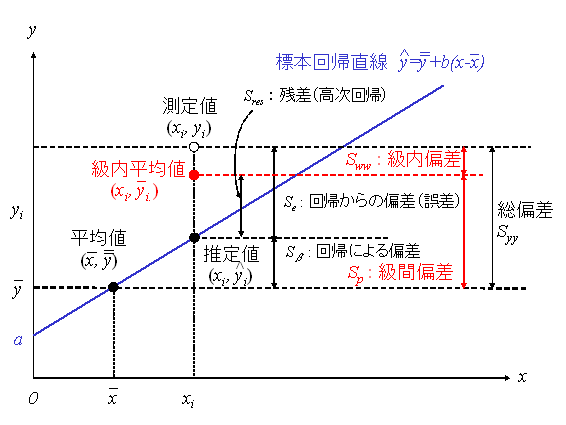
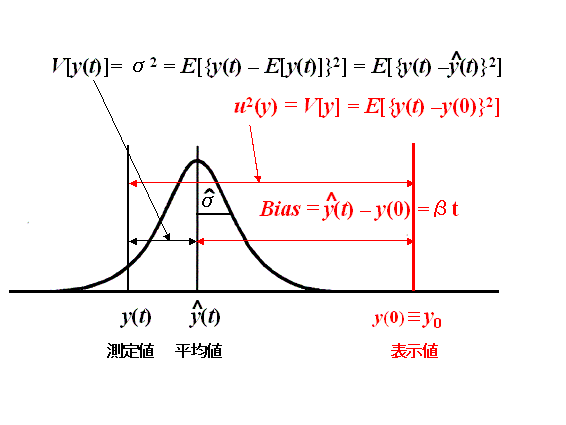
下図は、保存期間（内の任意の時刻における特定標準液の測定値のランダムな誤差分散と特定標準液の初期濃度および濃度のカタヨリとの関係を模式的に描いたものです。（具体的な中身は上式のにほぼ相当する）は時間依存性はないがカタヨリは明らかに時間に比例する項です。特定標準液を用いて特定二次標準液のjcss校正が校正保証期間（）内のどこで行われるかは任意（等確率）であるから、カタヨリに相当する不確かさ分散は

 

             

 

であり、したがって、jcss校正の不確かさ分散はこの時間平均項と時間に依存しないランダムな誤差分散を加えたもの

 

             

 

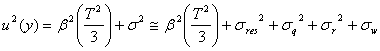
になります。厳密な意味ではは正規分布をした完全にランダムは誤差ではあり得ません。はあくまで標本データが１次回帰式で説明し得るとして処理したときの不適合度すなわち回帰残差（２次以上の高次の回帰を考慮すべきと言う意味での残差）であるから必ずしもランダムではあり得ないのです。でも、ここでは簡単のためも正規分布に従うランダムな誤差分散とみなしました。

 

 

いま、（は測定誤差）とおけば、不確かさの伝繙則よりであり、特定標準液の調製に関わる合成標準不確かさに相当する合成分散はであるから

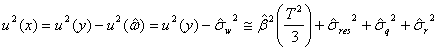
の式を使って特定標準液の不確かさが算出できます。

 

この手順による特定標準液の不確かさを求めるエクセルVBAマクロは以下からダウンロードできます。

 

                            三段枝分かれ実験回帰分析マクロ Ver.2.9  (reg3_29.xls)

 

　また、もし私たちが目標値としているのは質量比混合法で調製した標準液の濃度ではなく、測定値の総平均値（表示値）である場合には、不確かさの分散は

 

                           

 

となります。ただし、である場合は上式の代わりに

 

                           

 

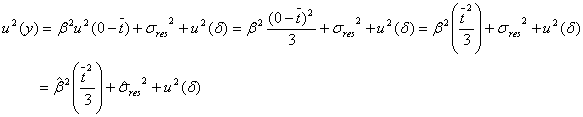
を表示値の不確かさの分散とします。また、（は測定誤差）とおけば、不確かさの伝繙則よりであり、特定標準液の調製に関わる合成標準不確かさに相当する合成分散はであるから

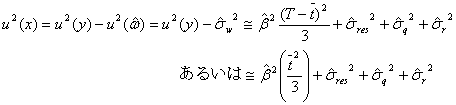
の式を使って特定標準液の不確かさが算出できます。

 

 

 

jcss校正時の値付けの不確かさ

 

jcss校正は質量比混合法で調製した特定標準液を用いて特定二次標準液を校正しようとするものであり、その値付けの測定法としてはガスクロマトグラフ分析法（GC分析法）がしばしば用いられます。

 

校正は、下図のように、被検溶液について特定標準液で５回繰り返し測定を行い、特定標準液の濃度とGC分析のピーク面積の比（）から被検溶液の濃度を求め、その平均値から被検溶液である特定二次標準液の濃度の推定値（）を求めるものとします。ただし、は被検溶液のi回目のピーク面積であり、は特定標準液のi回目のピーク面積とします。

GC分析の数学モデル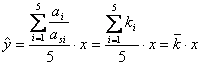　

　　　　　　ただし、GC分析の面積比 とした。　　　

単位を合わせるために相対合成標準不確かさを求める。

　であり、合成標準不確かさの一般式

              　　　

 

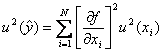
は、相対合成標準不確かさの一般式

 

              　　　　　（ここで、はの指数部である）

 

で表されるから、jcss校正時の相対合成標準不確かさは

             

              　　　

 

となる。

 

ただし、それぞれの標準不確かさに対応する分散は次の通りである。

 

（ここで、はGS分析のピーク面積比の測定誤差分散）

             

             

JCSS校正時の値付けの不確かさ

 

JCSS校正は、jcss校正で値付けされた特定二次標準液を用いて、実用標準液の濃度を値付けしようとするものです。したがって、もしJCSS校正時の分析方法がjcss校正時の分析方法と全く同じであったとすれば、その相対不確かさはjcss校正時の値付けの不確かさと全く同じ式で表現できることになります。すなわち、JCSS校正時の値付けの相対不確かさは

となりますが、この式の右辺にある分散にはjcss校正時に算出された相対不確かさの値を代入することになります。