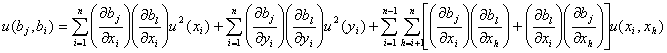
座標系に観測データをプロットして、近似曲線（直線近似をする場合が多いでしょうが）を最小自乗法（回帰分析）を使って求めたい場合が多々ありますが、通常の最小自乗法では観測データに不確かさ（統計学で教えるところのいわゆる標準偏差に相当するものであるが、最近の計量法では「不確かさ」という用語をもっと広い視野に立って使用します）がないという前提で解析することが多いのですが、観測データそのものに測定機器や測定方法あるいは繰り返し測定における不確かさがある場合の方が現実的なので、この不確かさを加味した最小自乗法による近似曲線のパラメータ（回帰係数）そのものやパラメータの誤差分散（不確かさの尺度となる統計量）を求めたいことがあります。このような座標系の観測データに不確かさがある場合の最小自乗法（回帰分析）を可能にしたのが、日本でもデミング賞で有名な米国のWilliam Edwards Deming博士が学位論文で発表したDemingの近似計算による最小自乗法（Demimg法回帰分析）です。原著：
W. E. Deming, Statistical Adjustment of Data, 1st ed., Dover Publications, Inc. (1964)
はすでに絶版であり、またその翻訳本も絶版となっているため、ここにその内容の概要（「Demingの方法（重み付き１次式の回帰分析）」と「１次式回帰分析と重みについて」）を紹介し、以下にその方法による回帰分析の計算プログラムの実例をいくつか掲載しました。
Deming法重み付き回帰分析エクセルVBAマクロ
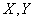（両座標に不確かさのある場合の最小自乗法）
|
|
Deming_0.xls （重みの定義：
|
Fitting_3.xls （重みの定義：
|
Fitting2_3.xls （重みの定義：
|
Fitting3_3.xls （重みの定義：
|
|
|
Fitting4_3.xls （重みの定義：
|
|
|
Fitting5.xls
（重みの定義：
|
|
|
deming_example.xls （重みの定義：
|
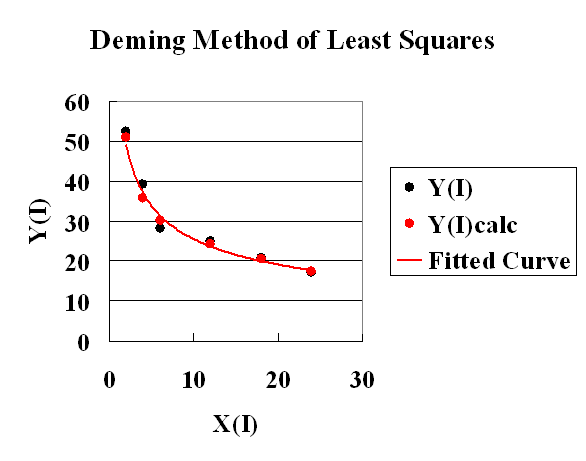
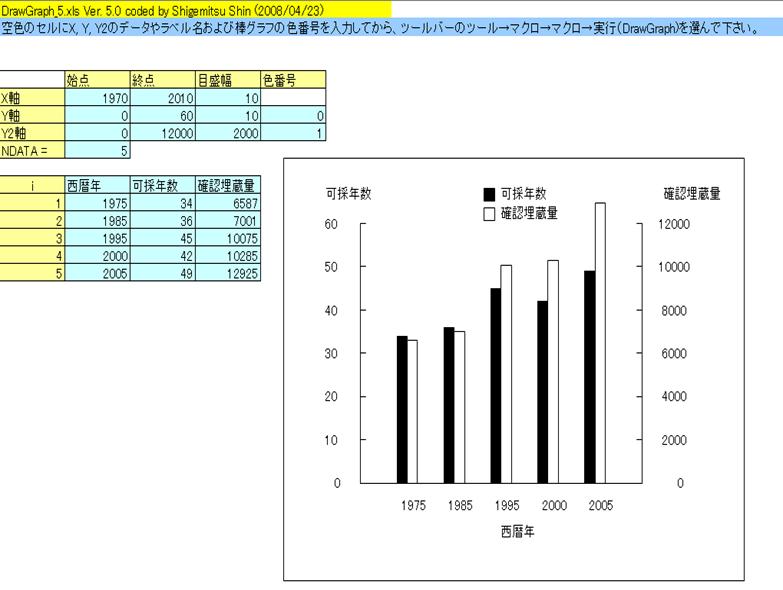
上図はExcelマクロDeming_0.xlsの計算結果の描画例
（注１） Fitting_3.xlsは、Deming_0.xlsを改良して、いろいろな関数にも適用可能にするためプログラミングしやすくしたマクロです。
マクロFitting_3.xlsを他の関数[観測方程式は
]に適用するには、このマクロのサブルーチン
の内容を書き換えるだけですみます。その場合は、
[
：データ数であり、
である] と
[
：パラメータ数] および
,
を書き換えて下さい。ここで、
は
番目のパラメータ（回帰係数）の近似値です。
たとえば、のような２次関数に適用する場合には、
であり、
となります。ただし、重み関数
にかかわるコマンド文
と
は関数が変わってもそのままです。このように、
は常に観測方程式そのものを表しています。
ただし、Fitting_0.xlsとFitting_3.xlsは観測データ
や
の重みを
と定義して計算しているので、あらかじめ回帰の残差分散
がわかっている場合でないと計算できません。そうでない場合は、Fitting4_3.xlsを使って下さい。後者の場合は重み係数の分散
を与える必要がありますが、この
（注２） 重みは、マクロFitting4_3.xlsの場合のように、
と定義するのが最も一般性があり、Deming_0.xlsやFitting_3.xlsの場合は
、あるいは、Fitting2_3.xlsの場合は
と定義した特殊な場合です。
重みの定義式中の分子
は
番目の標本データ（大きさ
個）の分散であり、標準不確かさ
は標準偏差
をデータ数の平方根
で割った統計学で言うところの標準誤差に相当する量です。したがって、
の場合に限り、
（注３） マクロFitting4_3.xlsは最も一般的な
次元多項式のDeming法回帰分析マクロです。
（注４） Fitting5.xlsはマクロFitting4_3.xlsの一変数の場合への応用例です。
（注５） マクロdeming_example.xlsはDeming法回帰分析の著者が書いた有名な本：
W. E. Deming, Statistical Adjustment of Data, 1st ed., Dover Publications, Inc. p. 218 (1964)
の中の例題を紹介がてらその解法をExcelでマクロ化したものです。この例題を勉強すれば、観測値の各点における標本数
と標本分散
からどのように
を求め、またそれらの値から
をどのように求めたらよいのかがわかります。また重みの任意の係数
このマクロでは例題の趣旨通りおよび
とした近似により最終的な計算処理をしていますが、マクロのその近似部分の記述箇所（***********で囲ってある部分）を削除すれば、例題の標本データから直接算出可能な
の値やその標準偏差
の値にはほとんど差がないことがわかります。すなわち、Deming法回帰分析では観測値である標本データの重みの定義式に関してはそれほど厳密性が求められるわけではないことがわかります。
Deming法重み付き回帰分析エクセルVBAマクロ２
（
座標間に相関がある場合の最小自乗法）
deming_ISO_cov.xls （重みの定義：
）
（参考） ISO 6143:2001(E)によれば、
座標共に不確かさのある重み付き回帰分析（Deming法）において、
座標間に相関がある場合については、回帰係数の誤差分散
のうち純分散の項（
）は係数行列の逆行列の要素として求められるが、共分散の項（
）は通常のDeming法では求めることができないため、ある任意の変数（
）によるある関数（
）の偏微分
と標準不確かさ
の積が一般的に次式
で近似できることから、Deming法で求められる
の最確値
（最小二乗曲線に乗っている計算値）に最初は
を加え、次に
個の値が得られますので、これらから上式と次式
から回帰係数の誤差分散
このような考え方に基づいてエクセルVBAで作成された回帰分析マクロがdeming_ISO_cov.xlsです。
Deming法重み付き回帰分析エクセルVBAマクロ３
− 粟屋-ISO方式Deming法改良型近似計算 −
（
POLYNOM_kojima.xls （重みの定義：
POLYNOM_kojima_linear.xls （重みの定義：
（参考） 上述のDeming法重み付き回帰分析（Fitting4_3.xlsなど）では近似計算がうまく行かないケース、たとえば
x
ux
y
uy
2
1
3
1
5
1
4
1
6
1
7
1
9
1
8
1
のように直線関係からかなりはずれた
および
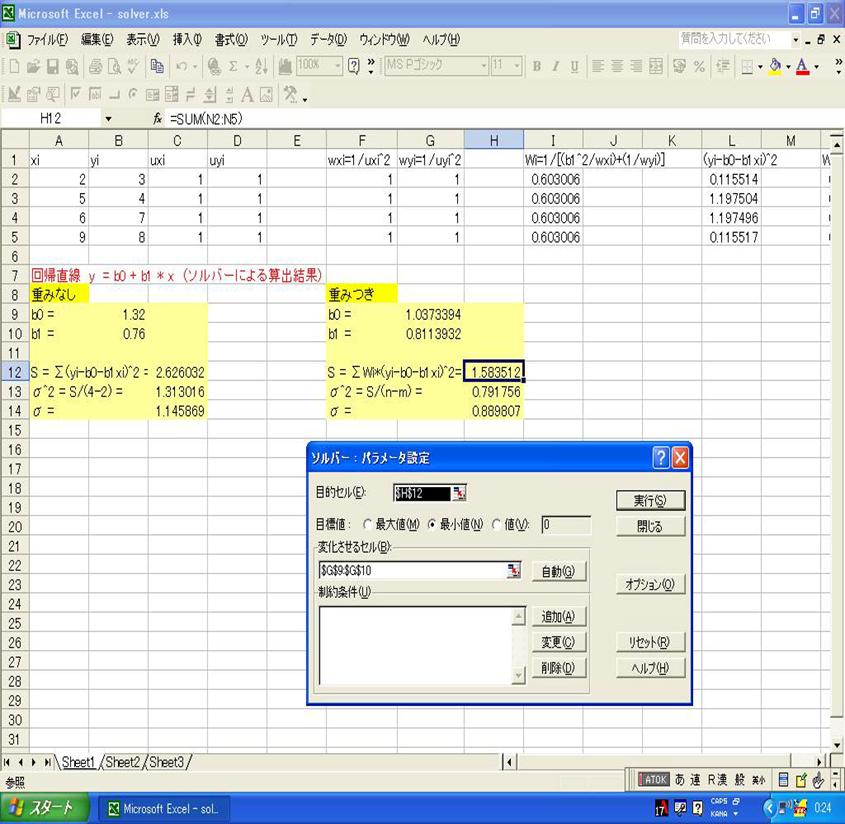
）が得られ、重み付けした意味がなくなります。そこで、Deming法を改良した粟屋（青山学院大学理工学部教授）-ISO方式（ISO 6143:2001(E)）近似計算を基にしてExcel VBAマクロで組んだプログラムPOLYNOM_kojima.xlsで、上述のデータを直線近似しますと、回帰係数を正しく算出（Excel標準の近似計算ソルバー（下図参照）による計算結果 [
および
] と一致）することができます。ただし、現実にはこのように理想回帰曲線から大きくばらついたデータに回帰分析を適用することは希だと思われるので、通常は普通のDeming法（Fitting4_3.xlsなど）で十分な近似計算ができます。
solver.xls （重みの定義：
もちろん、このような複雑な粟屋-ISO方式Deming法改良型近似計算マクロを使用しなくても、簡単な回帰直線近似の場合は、通常のDeming法回帰分析マクロFitting4_3.xlsなどで、観測方程式
の係数行列の偏微分係数項
の値
に、観測値そのままではなく、繰り返し近似計算ループで次々と求まる補正値
を考慮して補正した値
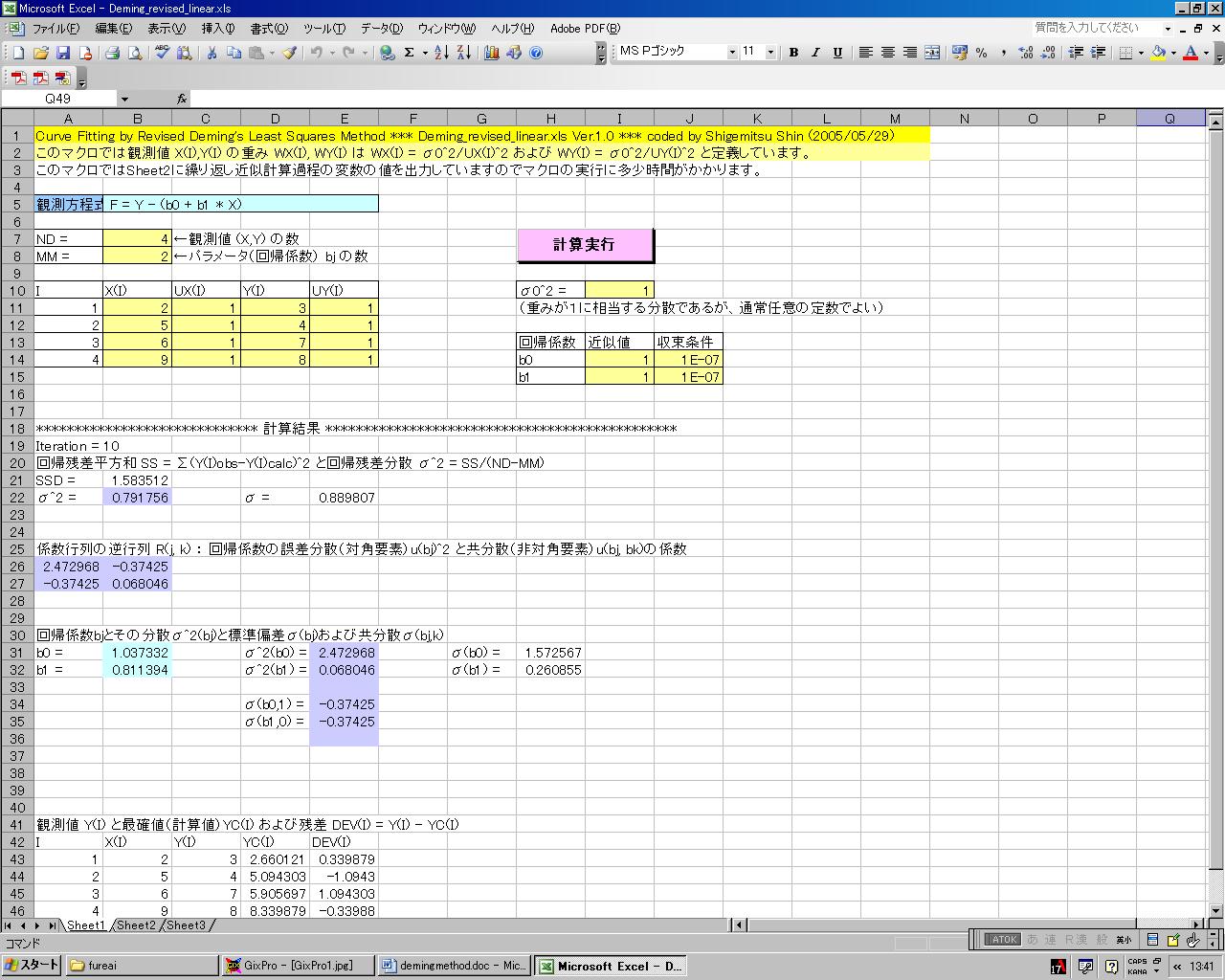
を代入することにより、回帰係数と分散・共分散を正しく求めることができます。実例は下記のマクロDeming_revised_linear.xlsを参照して下さい。
Deming_revised_linear.xls （重みの定義：
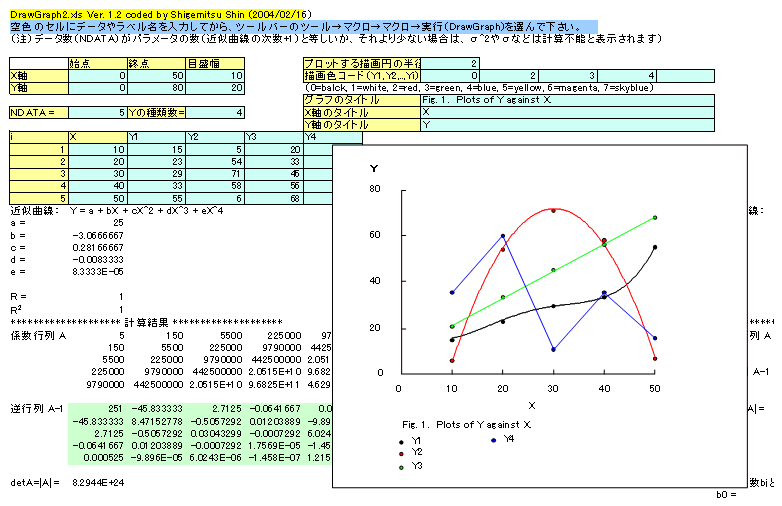
グラフ作成エクセルVBAマクロ（１次式/２次式/３次式近似曲線描画機能付き）
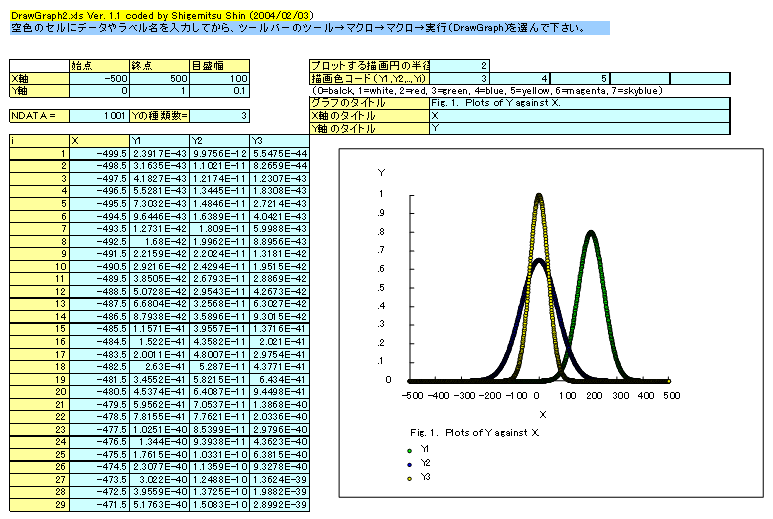
上記グラフ作成エクセルVBAマクロ２のサブルーチンDataGenration(ndata, x(), y())の内容を書き換えれば、任意の関数のグラフを描くことができます。下図はデフォルトで上記マクロのサブルーチンDataGenration(ndata, x(), y())に書き込まれている３種類の指数関数を自動描画した例です。 上記グラフ作成エクセルVBAマクロ３では横軸のX軸の目盛り間隔は実際の数字の幅でもあるいは上図のように実数字に無関係な等間隔でもプロットできます。
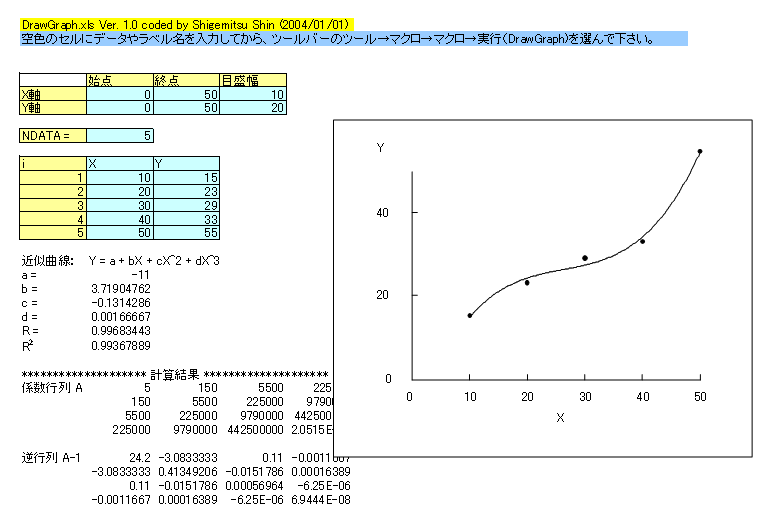
グラフ作成エクセルVBAマクロ２
（１次式/２次式/３次式近似曲線および折れ線描画機能付き）
グラフ作成エクセルVBAマクロ３
（２つのY座標軸を持つ棒グラフ）
