1次式回帰分析と重みについて
重みを考慮しない通常の回帰分析
通常私たちはデータの重みを意識することなく、1次式(![]() )回帰分析をExcelなどの統計ソフトで行い、回帰係数
)回帰分析をExcelなどの統計ソフトで行い、回帰係数![]() を求め、さらに回帰係数の分散
を求め、さらに回帰係数の分散![]() および
および![]() あるいは共分散
あるいは共分散![]() を正規方程式の係数行列式
を正規方程式の係数行列式![]() の逆行列式
の逆行列式![]() の対角項あるいは非対角項に回帰残差(
の対角項あるいは非対角項に回帰残差(![]() )の分散
)の分散
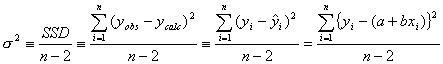
を掛けた式
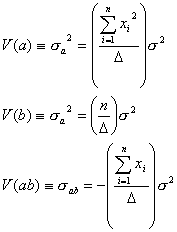
から求めています。ここで分母の![]() は、観測方程式
は、観測方程式![]() から導かれるパラメータ
から導かれるパラメータ![]() についての連立1次方程式(正規方程式)
についての連立1次方程式(正規方程式)
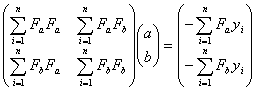
あるいは

すなわち
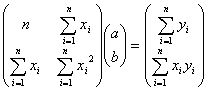
の係数行列式の値
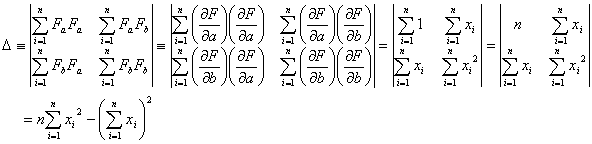
であり、その逆行列式![]() は
は
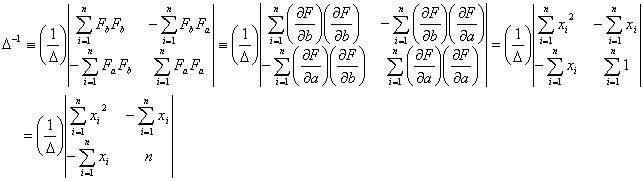
です。
![]() 座標には不確かさはなく
座標には不確かさはなく![]() 座標にのみ不確かさがある回帰分析
座標にのみ不確かさがある回帰分析
ここまでの式の中にはデータ![]() の重み
の重み![]() は一切入ってこなかったし、また顕わに考慮する必要も敢えてなかったわけです。しかしながら、1個1個のデータの信頼度(重み)が異なる場合には、上述のような観測方程式の係数行列式(ヤコビアンJacobian、関数行列式とも言います)では正しい回帰係数やその分散、共分散を求めることができず、ヤコビアンの中に重みを入れる必要があります。すなわち、正規方程式の係数行列は
は一切入ってこなかったし、また顕わに考慮する必要も敢えてなかったわけです。しかしながら、1個1個のデータの信頼度(重み)が異なる場合には、上述のような観測方程式の係数行列式(ヤコビアンJacobian、関数行列式とも言います)では正しい回帰係数やその分散、共分散を求めることができず、ヤコビアンの中に重みを入れる必要があります。すなわち、正規方程式の係数行列は

となり、したがって係数行列式![]() やその逆行列式
やその逆行列式![]() は
は

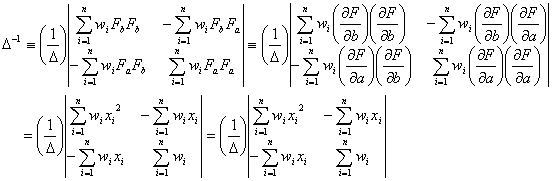
のように書き換える必要がります。このとき、最小二乗法を使って正規方程式を解くのに必要なデータは観測値![]() 以外にそのデータ(この場合簡単のために
以外にそのデータ(この場合簡単のために![]() 座標には不確かさはなく(すなわち重み=
座標には不確かさはなく(すなわち重み=![]() )
)![]() 座標にのみ
座標にのみ![]() によって異なる重みがあると仮定します)の重み
によって異なる重みがあると仮定します)の重み![]() を入力しなければなりませんが、その際の重み
を入力しなければなりませんが、その際の重み![]() の定義式は
の定義式は

でなければなりません。ここで、分母の![]() は観測点
は観測点![]() の母分散あるいはその推定値
の母分散あるいはその推定値![]() で代用される値です。ただし、
で代用される値です。ただし、![]() は平均値
は平均値![]() を求めるのに使ったデータ
を求めるのに使ったデータ![]() の個数
の個数![]() です。また、分子の分散
です。また、分子の分散![]() は単なる係数と考えてよく任意の数値を入れることが可能であり、またその次元も分母の母分散の次元
は単なる係数と考えてよく任意の数値を入れることが可能であり、またその次元も分母の母分散の次元![]() に合わせて
に合わせて![]() であると定義してもよく、あるいは単なる係数として無次元であると定義しても構いませんが、正規方程式を解く過程ではいずれかの次元および値にいつも一定に合わせておく必要があります。このように重みを定義すれば、求める回帰係数の分散
であると定義してもよく、あるいは単なる係数として無次元であると定義しても構いませんが、正規方程式を解く過程ではいずれかの次元および値にいつも一定に合わせておく必要があります。このように重みを定義すれば、求める回帰係数の分散![]() および
および![]() あるいは共分散
あるいは共分散![]() は
は
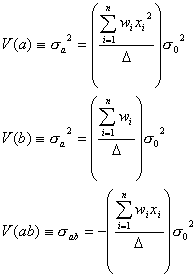
と表記することができます。ただし係数行列式![]() は
は

です。
したがって、通常の重みを考慮しない1次式(![]() )回帰分析においても、現実には
)回帰分析においても、現実には![]() 座標の重みを考慮しているのだが、
座標の重みを考慮しているのだが、

となるような重み![]() を定義しているため、回帰係数の分散
を定義しているため、回帰係数の分散![]() および
および![]() あるいは共分散
あるいは共分散![]() が、たまたま
が、たまたま
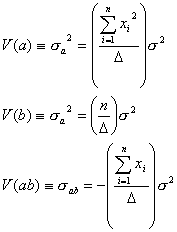

のように、係数行列の逆行列式![]() の対角要素に
の対角要素に![]() (この場合は結果的に回帰残差の分散に相当する)を掛けたものとして表記されることになるわけです。
(この場合は結果的に回帰残差の分散に相当する)を掛けたものとして表記されることになるわけです。
また、![]() 座標にのみ
座標にのみ![]() によって異なる重みがある1次式回帰分析において、重み
によって異なる重みがある1次式回帰分析において、重み![]() を、
を、![]() と置いて、
と置いて、
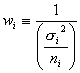
のように定義し直しすれば、求める回帰係数の分散![]() および
および![]() あるいは共分散
あるいは共分散![]() は
は
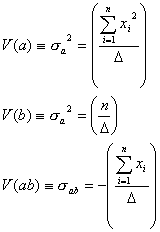

のように、見かけ上、回帰残差の分散項![]() は消失し、係数行列の逆行列式
は消失し、係数行列の逆行列式![]() の対角要素そのものになってしまうことに注意する必要があります。これらの式の証明は正規方程式の解から得られる回帰係数
の対角要素そのものになってしまうことに注意する必要があります。これらの式の証明は正規方程式の解から得られる回帰係数![]() の式を
の式を![]() と
と![]() について偏微分した感度係数
について偏微分した感度係数![]() や
や![]() を係数とする誤差伝搬則の公式
を係数とする誤差伝搬則の公式
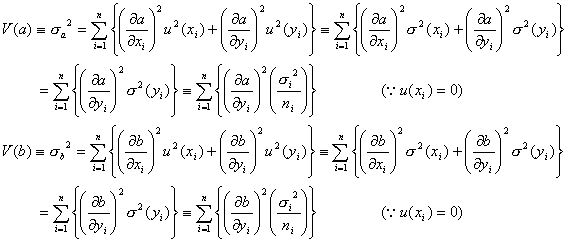
から直接導くことができます。
たとえば、回帰係数![]() は正規方程式の行列表現
は正規方程式の行列表現
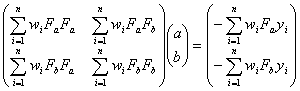
すなわち
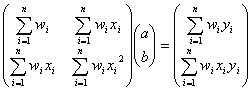
を使って
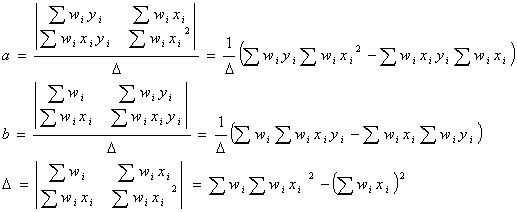
となります。したがって、回帰係数![]() の誤差分散
の誤差分散![]() は誤差伝搬則
は誤差伝搬則
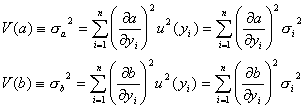
を使って以下のように求められます。ただし、重み![]() は
は
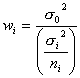
と定義します。ここで、![]() は任意に選ばれる既知の比例定数、
は任意に選ばれる既知の比例定数、![]() は観測値
は観測値![]() の
の![]() 座標の
座標の![]() 番目の観測点の平均値
番目の観測点の平均値![]() の誤差分散、すなわち
の誤差分散、すなわち
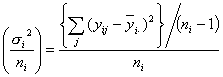
です。よって求める回帰係数の分散![]() および
および![]() は
は
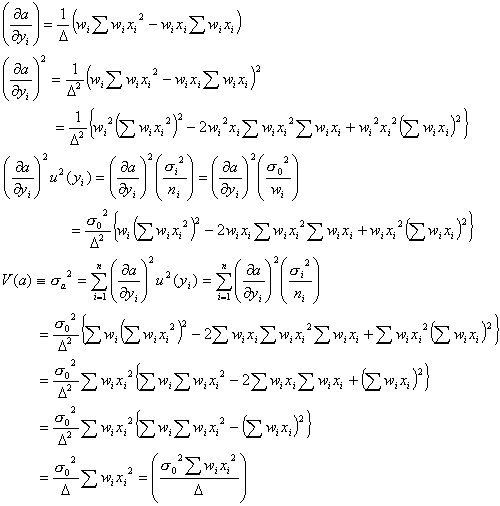

のようにして回帰係数の分散の式が誤差伝搬則より導かれます。
![]() 両座標共に不確かさのある回帰分析(Deming近似計算法)
両座標共に不確かさのある回帰分析(Deming近似計算法)
![]() 両座標共に不確かさのある回帰分析すなわちDeming近似計算法においても、重みが
両座標共に不確かさのある回帰分析すなわちDeming近似計算法においても、重みが![]() 座標だけでなく
座標だけでなく![]() 座標にもある場合に拡張しただけの話だから、残差
座標にもある場合に拡張しただけの話だから、残差![]() (
(![]() すなわち回帰係数
すなわち回帰係数![]() の近似値
の近似値![]() と対応する回帰係数の最確値(観測方程式
と対応する回帰係数の最確値(観測方程式![]() 上での計算値)
上での計算値)![]() との差)についての正規方程式の係数行列あるいは回帰残差の分散式において上述の
との差)についての正規方程式の係数行列あるいは回帰残差の分散式において上述の![]() 座標のみの重み
座標のみの重み![]() を新たな重み関数
を新たな重み関数![]() 、すなわち
、すなわち

で置き換えるだけでよいのですが、![]() と
と![]() の重みの定義の仕方を明確にしておかなければなりません。したがって、さきほどと同様にそれぞれの重みを一般化した式
の重みの定義の仕方を明確にしておかなければなりません。したがって、さきほどと同様にそれぞれの重みを一般化した式
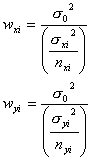
と定義した場合には、重み関数![]() は結局
は結局
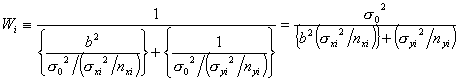
となるので、求める回帰係数の分散![]() および
および![]() あるいは共分散
あるいは共分散![]() は
は
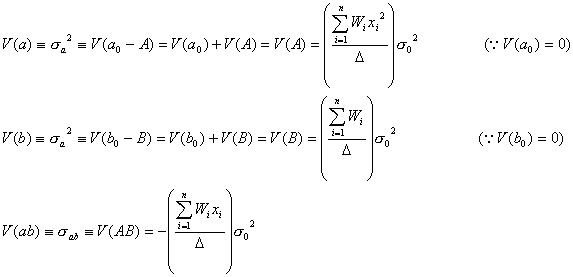
となります。ただし係数行列式![]() は
は
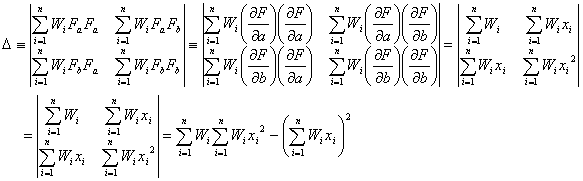
です。
したがって、上述の「![]() 座標には不確かさはなく
座標には不確かさはなく![]() 座標にのみ不確かさがある回帰分析」の場合と同様に、重みの係数
座標にのみ不確かさがある回帰分析」の場合と同様に、重みの係数![]() としてたまたま回帰残差の分散そのもの
としてたまたま回帰残差の分散そのもの![]() を採用した場合には、求める分散式は
を採用した場合には、求める分散式は
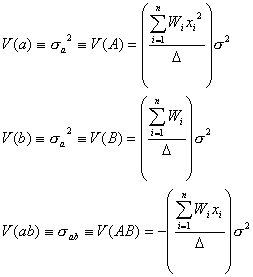
となり、![]() と定義した場合の分散式は
と定義した場合の分散式は
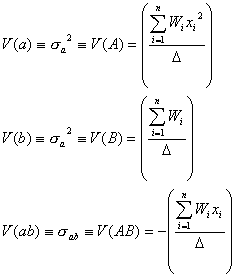
となります。ちなみに、Deming近似計算法における正規方程式の行列表示は
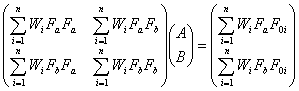
です。ただし、観測方程式のテーラー展開の初項![]() は
は
![]()
のように、回帰係数の近似値![]() および観測値
および観測値![]() を用いて表される値です。
を用いて表される値です。