津波をコンピュータ上で再現する
地震時に起きる海底地形の変化(地殻変動や海底の地すべり)により、海面も変化します。その変化が波となって周囲に広がります。この広がる様子を、コンピュータによって計算(再現)することができます。
津波シミュレーションによって再現された869 年貞観津波が伝播する様子



『格子』に区切って津波を計算する
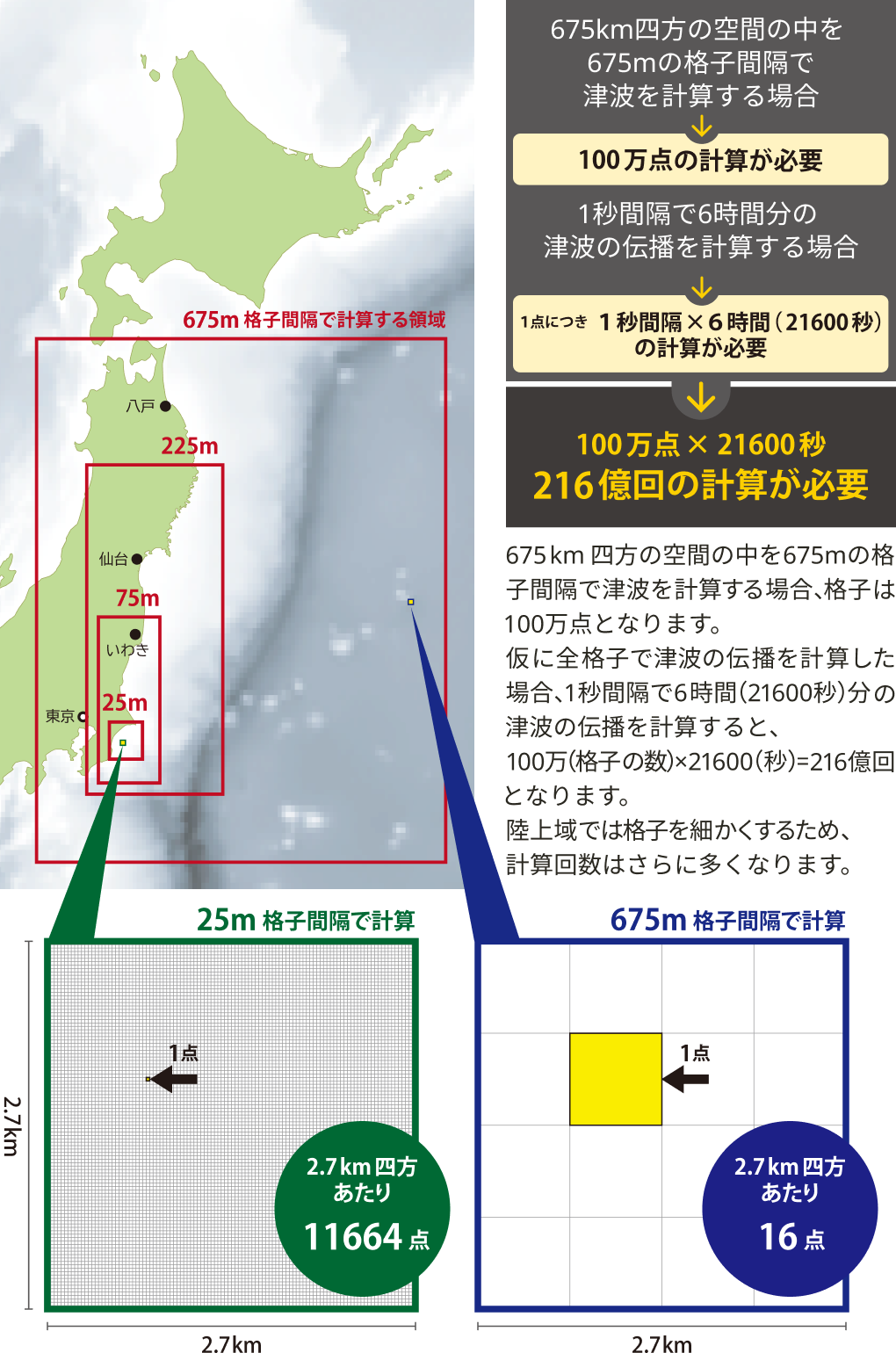
津波の計算方法の一つとして、計算したい領域を細かい格子(規則的に並んだ区切り)に分割し、すべての格子において津波の伝播を計算するという方法があります。この計算する格子は、陸上の浸水計算を行う領域に向かって段階的に細かくしていく必要があります。
津波が広がる速さは水深と関係があり、沖の深い場所ではジェット機くらい、陸上近くではウサイン・ボルト選手が全力疾走するくらいの速さで伝播します。
このように速さが違いすぎる波を再現しようとすると、同じ格子間隔では波を正確に把握できなくなります。
例えば、沖では675mの格子間隔で水位を計算すれば良いですが、海岸に近くなると比較的遅い複雑な波となるため、細かい格子が必要となります。
はじめから全体を細かい格子で区切ると、計算回数が非常に多くなってしまいます。浸水域を細かく知りたい場所があれば、そこに近づくにつれて計算する格子を細かくするほうが、効率よく計算できます。
地震をあらわす数字【断層パラメータ】
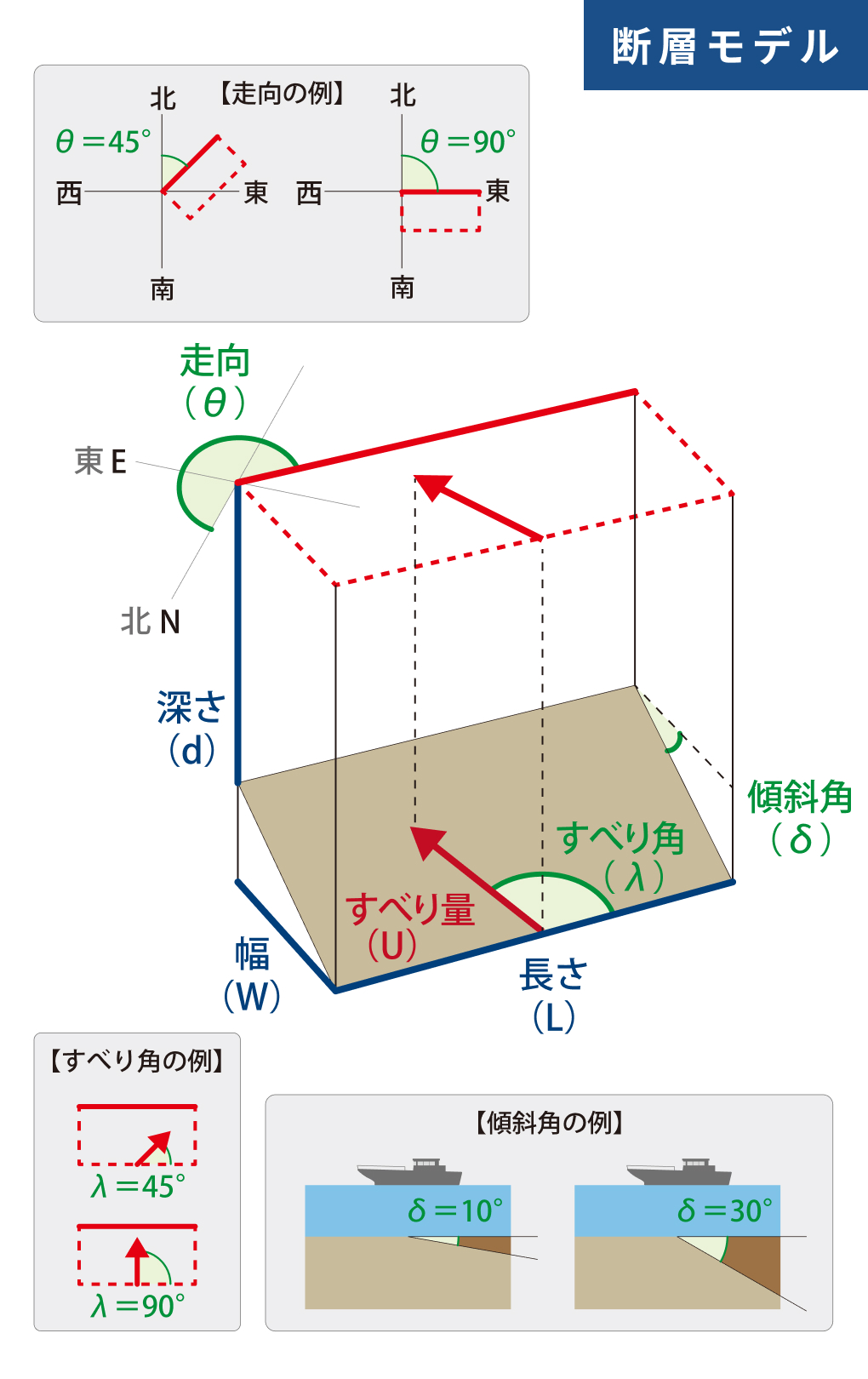
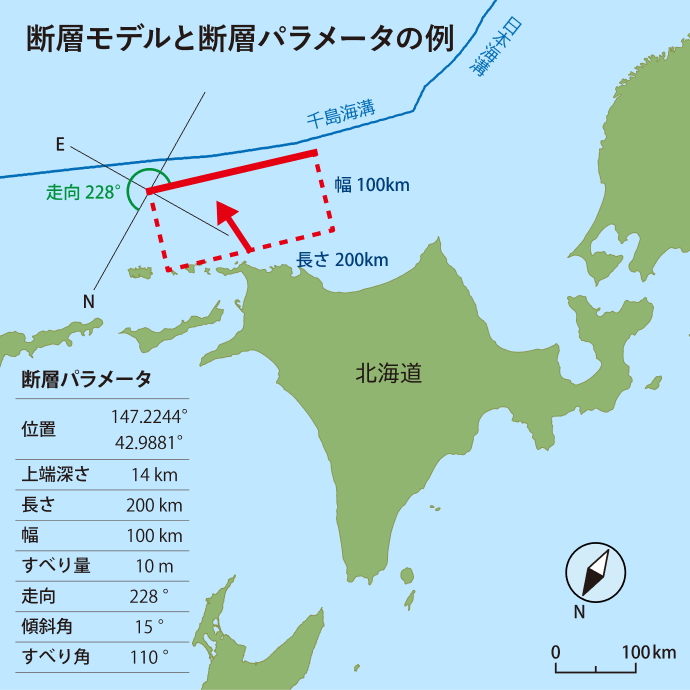
海底の地殻変動を起こす地震の規模と場所は、多くの場合、長方形を使って表現します(断層モデル)。この時、「断層パラメータ」とよばれる9つの値でその特徴を示します。
断層パラメータ
| パラメータ | パラメータを 表現する文字 |
単位 | |
|---|---|---|---|
| 位置 | N E | 度 | 矩形の位置はプレート境界に沿って配置される場合が多い |
| 上端深さ | d | km | 上端の深さはプレート境界に沿って配置される場合が多い |
| 長さ | L | km | 走行方向の長さ |
| 幅 | W | km | 傾斜方向の長さ |
| すべり量 | U | m | ずれの大きさを表す量 |
| 走向 | θ | 度 | 矩形の向きを表す角度。断層下端から上端を見た時の左上端を中心として、断層上端が北から時計回りに何度回転しているかを表す量 |
| 傾斜角 | δ | 度 | 矩形面の水平面に対する傾きを表す角度 |
| すべり角 | λ | 度 | 矩形領域が地震時にどの方向に動いたか(ずれの方向)を表す角度 |
地殻変動量
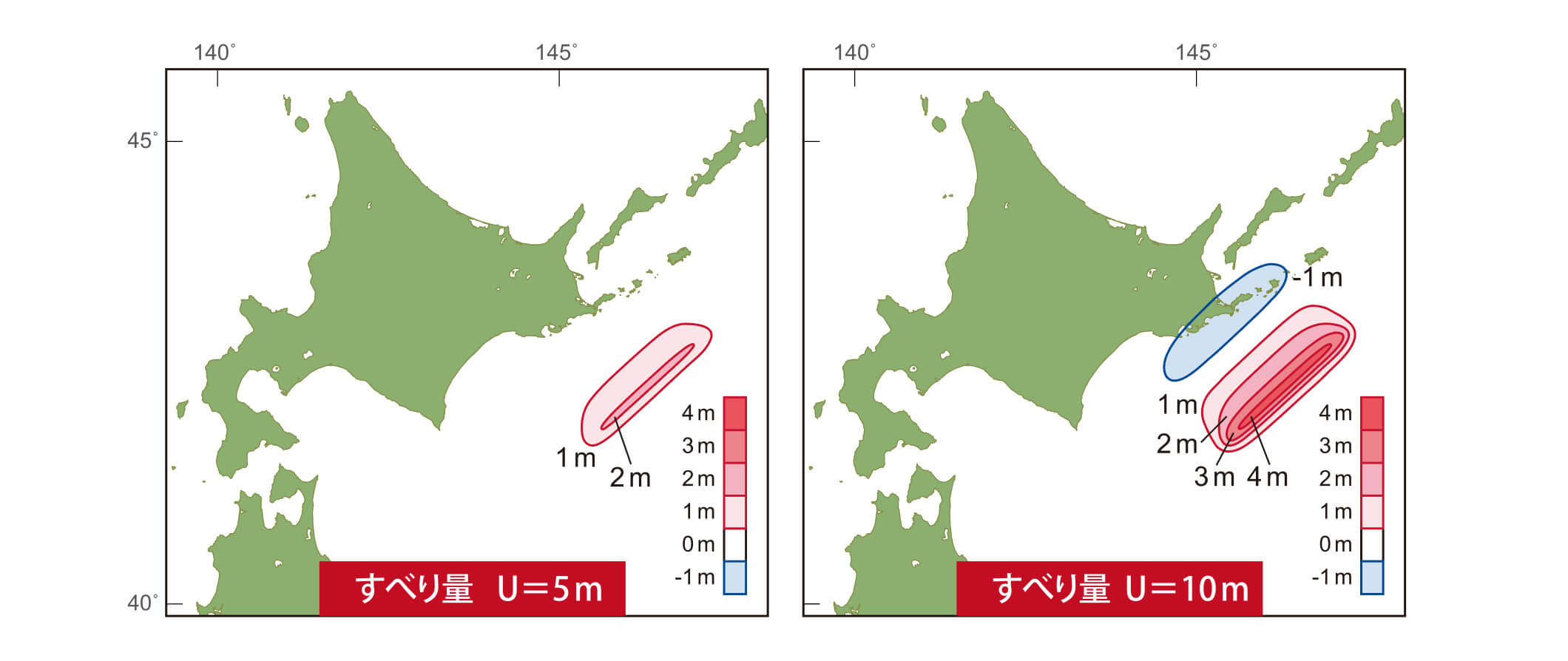
下の例は、断層パラメータのうち、すべり量(U)だけ変えてみた場合です。すべり量が2倍になることで、地震の時の地殻変動量も2倍になり、発生する津波の高さが2倍となります。
津波の波長・周期と浸水範囲
津波の波長と周期
「大きな津波」と聞くと波の「高さ」に注目しがちです。しかし、その高い津波が平野の奥まで浸水するかというと、必ずしもそうではありません。
九十九里浜など広い平野で浸水範囲に大きな影響を与えるのは、津波の「波長(波の山と山、谷と谷の距離)」です。波長が長いとそれだけ水位が高い時間が長く続くので、津波が内陸まで浸水します。
波の「周期」という言葉もよく使われます。周期は、波の山が通過して、次の山が来るまでの時間です。波長の長い波は、周期が長いことを意味します。海で普通に見られるうねりの周期は、中程度のもので8 秒から11秒くらいと言われています。うねりと比較すると津波の周期は非常に長くなります。
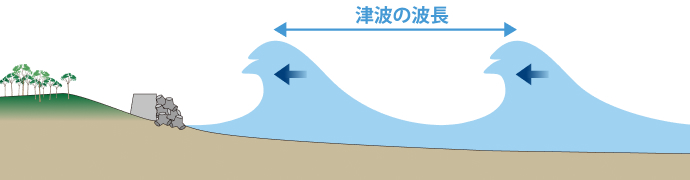
波長が短い津波
堤防を超える可能性がありますが、海水を内陸に運ぶ時間が短いため、浸水範囲は限られた範囲になることが多いです。波の周期は10分程度です。
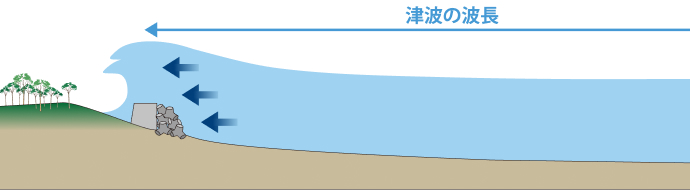
波長が長い津波
波長が長く、さらにその高さが堤防を超える場合、内陸奥深くまで浸水する可能性があります。波の周期は数10分になることがあります。
波長の違いからくる浸水範囲の違い
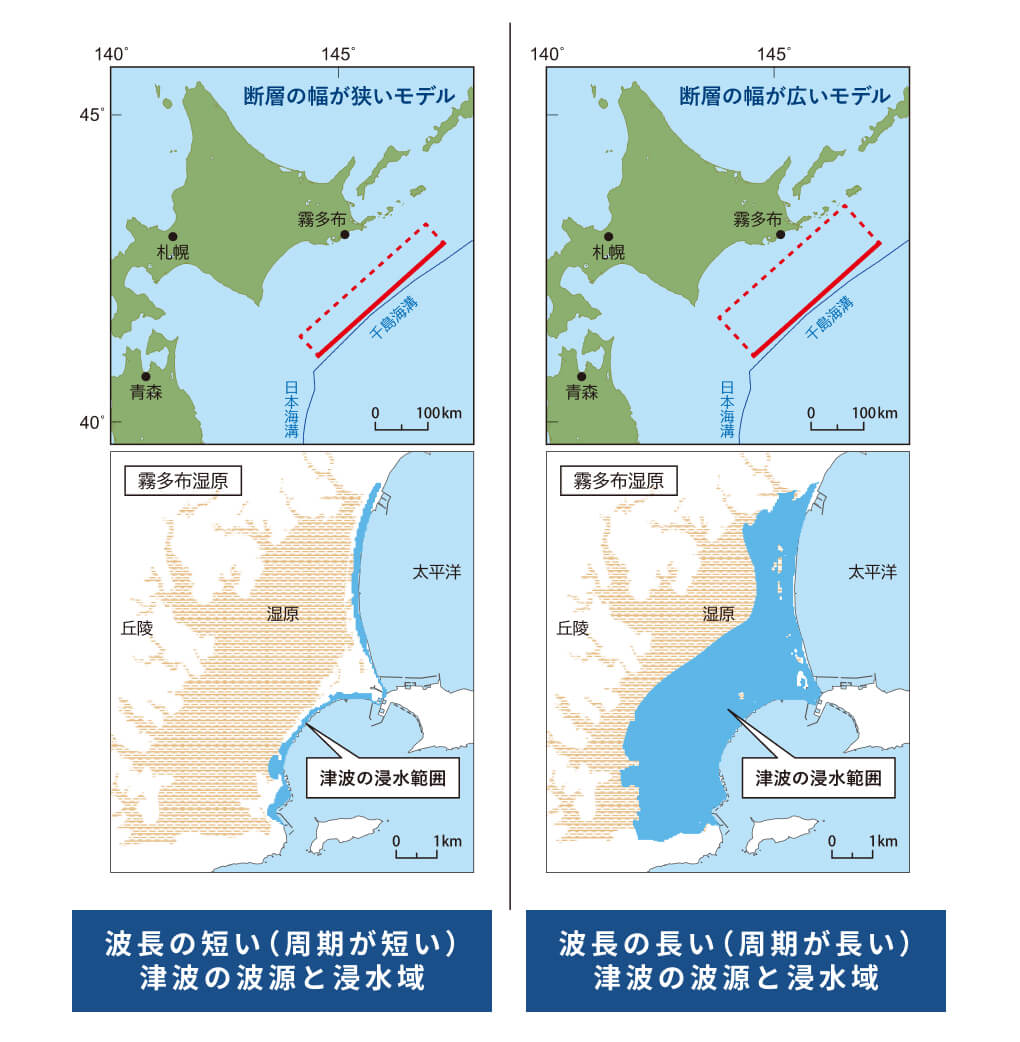
千島海溝南部で断層の幅の違う2通りの断層モデルを考え、コンピュータシミュレーションを行った例が右図となります。
断層の幅の違いによって発生する津波の波長と周期が違うため、浜中町霧多布地域での浸水範囲が大きく違うことがわかります。
波長と周期の違いを生み出す「断層の幅の違い」が、非常に重要であることを示した良い例と言えます。
本⾴は、伊尾⽊ほか(2023)GSJ 研究資料集no.744 を改変したものです。
