2.5.システム幾何補正 概要：システム幾何補正は衛星の付属データとセンサの補足情報のみを用いて、検出素子の視線ベクトルから座標変換等の手法により観測地点を算出する処理である。観測地点は地表と視線ベクトルの延長線の交点として求められる。センサと衛星の技術情報は、それぞれセンサの補足データ（supplementary data）、衛星の付属データ（ancillary data）と呼ばれている。選ばれるベクトルの数を除けば、システム幾何補正は3つのサブシステムに対して殆ど同じである。Figure 2-6にシステム幾何補正のフローを示す。 画像データは軌道直交方向、軌道平行方向共にブロックに分割される。ブロックの大きさは以下の通りである。 VNIRバンド 1, 2, 3N： 410 x 400 ピクセル VNIRバンド 3B： 500 x 400 ピクセル SWIR全バンド： 20 x 20 ピクセル TIR全バンド： 72 x 70 ピクセル これらの大きさは、軌道直交方向に対しては焦点面上の光学像の歪み、軌道平行方向に対しては衛星の姿勢安定度を考慮して決められた値である。座標変換は選定された検出素子の視線ベクトルに対してのみ行われる。選定された検出素子の数は、VNIR, SWIR, TIRに対してそれぞれ11、104、11である。これらは、軌道直交方向のレベル0画像の各ブロックの隅の数に相当している。軌道直交方向の端ではダミーピクセルを導入してブロックが完結するようにしている。 システム幾何補正は以下のような幾つかの部分に分割されている。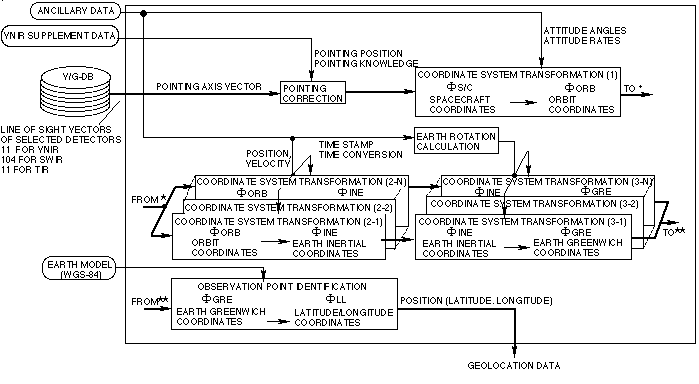 (1) ポインティング補正 (2) 衛星航法基準座標系から軌道座標系への変換 (3) 軌道座標系から地球慣性座標系への変換 (4) 地球慣性座標系から地球固定座標系（地球グリニッジ座標系）への変換 (5) 地球表面と視線ベクトルの延長線との交点の決定 Figure 2-6 システム幾何補正のフロー ポインティング補正：幾何データベースファイルに格納されている視線ベクトルはポインティング位置が直下の場合の値である。ポインティングを直下以外にした場合には、センサ補足情報に含まれているポインティング角度データを用いて、視線ベクトルをポインティング軸に対して回転させる変換が必要になる。 ポインティング角度 b の時の視線ベクトル S0 からS への変換は次の式でなされる。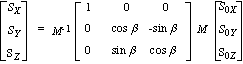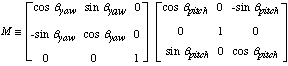 (2-1) ここで、 S0x, S0y, S0z：ポインティング前の視線ベクトル S0 のx, y , z 成分 Sx, Sy, Sz：ポインティング前の視線ベクトル S のx, y , z 成分 (2-2) 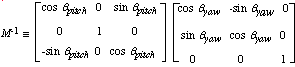(2-3) 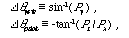(2-4) (2-5) Px, Py, Pz：NBR座標系におけるポインティング軸の単位ベクトルのx, y, z成分 Figure 2-7にポインティング軸とNBR座標系の関係を示す。角度DqyawとDqpitchはそれぞれポインティング軸をXNBR 方向に合わせるためのヨーとピッチの回転角度である。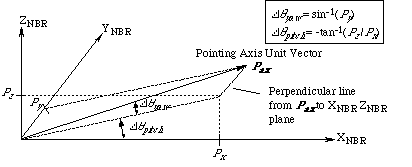 Figure 2-7 NBR座標系でのポインティング軸ベクトル 衛星座標系から軌道座標系への変換：衛星座標系（正確には衛星航法座標系）は軌道座標系と少しばかり異なっている。その差は衛星の姿勢制御の精度に由来している。姿勢制御の誤差は衛星付属データの中に格納されている。軌道座標系は右手直交座標系である。+ｚ軸は衛星の重心から地球の中心に向けた方向、+ｙ軸はｚ軸と衛星の瞬時速度ベクトルの両者に直交した方向、+ｘ軸は上記ｚ軸とｙ軸とともに右手直交座標系を形成する方向である。この処理は衛星付属データの姿勢角と姿勢角速度を用いて行われる。 衛星航法座標系における視線ベクトルは衛星付属データ中の姿勢角データを用いて以下のような変換式で軌道座標系に変換される。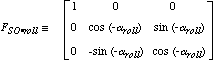 SOR = FSO・yaw FSO・pitch FSO・roll S , (2-6) ここで、 S：衛星航法座標系で表現した視線ベクトル、 SOR：軌道座標系で表現した視線ベクトル、 (2-7) 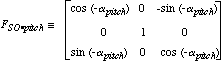(2-8) 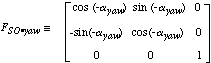(2-9) aroll, apitch , ayaw：衛星付属データに含まれる衛星姿勢データのロール、ピッチ、ヨー成分の角度。 軌道座標系から地球慣性座標系への変換：この変換は、軌道座標系から慣性空間における地球中心座標系への変換である。衛星の進行に基づいて、2次元アレイベクトルがこの変換の結果として得られる。アレイ次元は観測時間に依存している。即ち、衛星進行方向のアレイ次元は観測時間中に衛星の進行方向に沿って観測されたピクセルの数に相当する。軌道座標系から地球慣性座標系への視線ベクトルの変換は衛星の位置と速度データを用いて行われる。Terraの制御は平均J2000.0系（西暦2000年1月1日正午の座標系）を用いてなされるため、より正確な地表ピクセル位置決定のために再差運動と章動が考慮される。 軌道座標系から地球慣性座標系への視線ベクトルの変換は衛星の位置と速度データを用いて次の式で行われる。 SEI = FOI SOR, (2-10) そこで、 SOR：軌道座標系における視線ベクトル、 SEI：地球慣性座標系における視線ベクトル、 FOI = (Tx Ty Tz ), (2-11) Tx Ty Tz： 軌道座標系のx, y, z 軸方向の単位ベクトルの地球慣性座標系での表現であり、以下のように定義される。 Tx = Ty x Tz Ty = unit (-R x V ) Tz = unit (-R ) (2-12) R ,V：地球慣性座標系で表現した衛星の位置と速度ベクトル より正確な解析のためには西暦2000年1月1日正午を起点とした地球歳差運動マトリクス P と章動運動マトリクス N を上述の計算で求めた地球慣性座標系で表した視線ベクトル SEI にさらに演算する必要がある。 地球慣性座標系から地球固定座標系への変換：この変換は地球中心座標系から地球の自転に相当する角度分を考慮した地球固定座標系への変換である。正確な地球自転を解析するために衛星から供給されるUTC時刻はUT1に変換される。 地球慣性座標系から地球固定座標系表現への視線ベクトルの変換は次のような式でな行われている。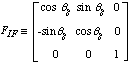 SEF= FIF SEI (2-13) ここで SEI：地球慣性座標系で表現した視線ベクトル、 EF：地球固定座標系で表現した視線ベクトル、 (2-14) qg：グリニッジ真恒星時角 地表観測位置の決定：観測地点は地表と視線ベクトルの延長線の交点から決定される。地表モデルとしてWGS-84が用いられる。 まず、視線ベクトルの延長線は次の式で表現できる。 x = X + SEF・x r y = Y + SEF・y r z = Z + SEF・z r (2-15) ここで、 SEF・x , SEF・y , SEF・z：地球固定座標系における視線ベクトルSEF のx,y, z 成分, X, Y, Z：地球固定座標系における衛星位置のx, y, z 成分, r：パラメーター。 地球の表面は次の式で与えられる (x2 + y2)/a2 + z2/b2 = 1 (2-16) ここで、 a = 6378136m (赤道上での地球半径--WGS-84の場合), b = a (1 - f ) (極での地球半径---WGS-84の場合), f = 1/298.2572 . (2-17) 交点は、(8.2-19) 式と(8.2-20)式より求められる。観測地点を Px, Py, Pz で表わすと地心緯度 y と経度 l は次の式で与えられる。 y = tan-1{Pz /(Px2 + Py2)1/2} l = tan-1(Py /Px ) (2-18) (2-19) システム補正の精度：Table 2-2に、衛星とセンサの両方を考慮したシステム幾何補正の結果としての地表ピクセル位置の確度を示す。総合的なASTERの地表ピクセル位置決定確度は、衛星の位置確度、姿勢確度、ASTERのポインティング確度によって決まる。SWIRとTIRはレベル1処理中にVNIRバンド2に対するピクセル合わせが行われるので、VNIRの地表ピクセル位置確度のみが重要である。 Table 2-2 地表ピクセル位置確度 Specification Dynamic Error (3s) Static Error (3s) Along-track (m) Spacecraft*1 ｱ342 ｱ28 ｱ111 ASTER/VNIR ｱ205 ｱ38 ｱ99 Total ｱ431*2 ｱ47 ｱ149 Cross-track (m) Spacecraft*1 ｱ342 ｱ25 ｱ148 ASTER/VNIR ｱ205 ｱ48 ｱ103 Total ｱ437*2 ｱ54 ｱ180 *1: Three non-optimal 9 minute TDRS contacts per orbit, GJM2 Geopotential 30 x 30), solar flux of 175, 5 % Cd error, TDRS ephemeris error of 75 meters. Two star trackers, rigid body/low frequency pointing knowledge error removed *2: Slightly larger than RSS of two values (Spacecraft and ASTER instrument), because of unallocated margin. システム幾何補正精度は、通常運用中においても、GCPを用いた幾何検証活動を通し て定期的に確認される。