GSJトップページ > 研究紹介 > 重点プロジェクト・重点研究課題 > 原子力安全規制支援研究プロジェクト > 技術資料2012 > Appendix > 岩盤水理特性関連評価手法

技術資料2012 Appendix 岩盤水理特性関連評価手法

採水法

| ↑ top | 採水法 | 現位置調査 | 岩石の移流拡散特性 |

原位置採水

原位置採水が行なわれる対象は，高い透水性を持つ多孔質媒体と‘水みち’である断層・節理などである．高い透水性を持つ多孔質媒体を対象とした原位置採水では採水区間を比較的長く設定することが多いが，‘水みち’である断層・節理を対象とした原位置採水では採水区間を短く設定し，採水対象外の断層・節理などをできるだけ含まないようする．そのため‘水みち’を対象とした原位置採水においては採水対象となる断層・節理などによる割れ目を探査・決定する手法が重要となる．また，原位置採水で一般的に用いられる採水法についても記述する．

 

原位置採水深度の探査・決定手法

断層や節理などを対象とした採水調査では，ボーリング孔壁に存在する割れ目の中から水みちとなる透水性割れ目を検出し，その深度で採水を行なう必要がある．地層処分に係る掘削調査では，掘削流体による地下水の汚染の影響をできる限り低減させるために’水みち’（候補）と同定された透水性割れ目に対して掘削直後に速やかに原位置採水調査・水理試験を行う必要があり，採水深度の探査･決定手法は迅速・簡便に行うことが可能な調査技術であることも重要である．電気伝導度検層法は原理的に最も優れた水みち調査法であるが，孔井内の水を脱イオン水に全て置換する必要があり，また採水試料に関して掘削水と脱イオン水の混入割合をそれぞれ独立に推定する必要があるなど，掘削調査における採水深度の探査･決定手法としては実用上の問題が多い．電気伝導度検層法はむしろ全掘削終了後に水みちとなる透水性割れ目の見落としの有無を判断する手法として，非常に有効な方法である．
現在のところ，処分対象となるような地下水流速の極めて遅い地層・岩体中の透水性割れ目を検出する手法は電気伝導度検層法以外に存在しない．しかし，透水性割れ目の候補となる開口割れ目を検出する手法は複数存在する．開口割れ目の検出法としては，孔壁の形状を観察・測定する光学的観察法・超音波測距法と開口割れ目の物理的特性を検出するVSP法を用いたチューブ波検層・音波検層などがある．なお，開口割れ目の開口度と透水性の間には一定の関係があるものの，開口幅0.5mm以下の開口割れ目が極めて透水性の高い透水性割れ目であった事例が存在することから，物理検層法を用いて開口割れ目の検出を行なうことが望ましい．

また，泥水を用いた掘削調査では孔壁に泥壁が形成されるため，大規模な湧水箇所などを除けば，前出の開口割れ目探査法のいずれも適用できず，採取されたコア試料のみを用いて採水箇所を決定する必要がある．
①電気伝導度検層：孔井内の孔内水を脱イオン水に全て置換し，水みちとなる透水性割れ目から孔内に流入した地下水により透水性割れ目周辺の孔内水の電気伝導度が上昇することを利用して，透水性割れ目を検出する検層法であり，原理的に最も優れた採水位置決定法である．

②光学的観察法：ボアホールカメラを用いた孔壁の光学的観察により開口割れ目を検出する手法である．ボアホールカメラの分解能は，孔周0.5度以内，深度方向分解能0.25mm以内と孔井検層法の中で最も高い分解能をもつ．孔壁崩壊部から得られる光学的データは単独では解析不能であり，超音波測距法などによる孔壁間距離のデータが必要である．また，孔壁が深く崩壊している場合は暗い光学像しか得られず．解析不能な場合がある．現在日本国内では２つの光学的観察法が存在するが，両手法の解像度や割れ目の解析結果に大きな差異は存在しない．

③超音波測距法：ボアホールテレビューアを用いた孔中心と孔壁間の超音波測距により開口割れ目を検出する手法である．孔壁崩壊部が単純な形状の場合は孔中心と孔壁間の超音波測距を得ることができるが，複雑な形状の場合は測定データの信頼性は低い点に留意する必要がある．現在使用されているボアホールテレビューアは，孔壁崩壊部に対して十分な発信強度と空間分解能を有していない．

④VSP法を用いたチューブ波検層：地表発振源（固定），孔井内ハイドロフォンレシーバを用いたVSP検層で捕捉されるチューブ波が，孔壁の開口割れ目から発生することを利用した開口割れ目検出法である．チューブ波検層法の探査精度は，深度方向精度10cm以内/300m，チューブ波発生深度分解能10cm以内である．

⑤音波検層：孔井内発振源，孔井内受振器を用いた音波検層では，孔井内発振源から発生したP波が孔壁の開口割れ目を通過する際に遅延され，P波到達時間が遅れることを利用した開口割れ目検出法である．音波検層法の探査精度は，深度方向精度5cm以内/600m，開口割れ目検出深度分解能5cm以内である．

 

原位置採水法

掘削調査においてボーリング掘削と組み合わせて行なうことのできる原位置採水法は，基本的にパッカー採水法のみである．一般的にはダブルパッカー法による採水が行なわれるが，孔底に近い区間を採水対象とする場合はシングルパッカー法による採水が行なわれる場合もある．パッカー採水においては，パッカー区間内に存在する孔内水を予備採水により排水し，原位置水試料に対する孔内流体の混入を低減させる必要がある．原位置水試料に対する孔内流体の混入は1%程度以下であることが望ましい，また，孔内流体の混入率が5%以上の場合，原位置水試料の水質・同位体組成などを適切に評価できない可能性が高い．予備採水はパッカー区間の容積の20倍程度以上を目安に行なうことが望ましい．

なお，地層・岩体の地下水流速が一定以上の速度を持つ場合は，掘削終了後に多段のパッカーを埋設し，掘削流体の影響がなくなるまで一定期間放置した後に採水を行なうマルチパッカー法による採水も可能である．

 

コア採水

コア採水が行なわれる対象は，透水性が低く原位置採水が困難な多孔質媒体である．掘削コアに含まれる間隙水を，遠心法もしくは圧密抽出法により抽出する．遠心法および圧密抽出法で間隙水を抽出する場合，抽出圧は自由水の抽出限界以下に設定しなければならない．圧密抽出法により間隙水を抽出した報告例の多くでは，自由水の抽出圧よりも高い結合水レベルの抽出圧で間隙水を抽出しており，それらの抽出水の水質・同位体組成をもとに地下水流動を論じることは原理的に誤っている．なお，原位置採水と同様にトレーサーにより掘削流体の混合量を評価する必要がある．

原位置における水理・物質移行特性調査

| ↑ top | 採水法 | 現位置調査 | 岩石の移流拡散特性 |

地下深部において物質は主に移流・拡散現象により移動するが，どちらの現象が支配的となるかは，その場における地下水流動の速度に依存する．従って，処分領域からの移行経路と移行プロセスで支配的な現象を予想するためには，地下水流動系の概略を把握することが必要となる．地下水流動系は，地形，地層や岩体あるいは断層などの分布に規制される地質構造，地層や岩体の透水性（透水層／不透水層）・地下水の水位ポテンシャル・地下水の涵養−流動−流出機構などの水文地質構造を基に，地下水系の流向・流速や間隙水圧・透水性などのデータに基づき概略的に評価される．概要調査段階では，概要調査地域全域の地下水流動場を詳細に特定することは不可能であるが，掘削調査に際してはボーリング孔が掘削される水理地質ユニット毎あるいは境界となる断層などの地下水の流向・流速や間隙水圧・透水性に係るデータを取得し，処分深度までの地下水流動を実データに基づき確認する必要がある．核種移行解析においては，水理地質ユニット毎の透水特性や拡散などの物質移行特性のデータが必要であり，原位置測定が可能な項目については原位置で，原位置測定が不可能な項目については室内試験により測定・試験を行なう必要がある．

物質移行解析では，複雑な地質体を連続体モデル／亀裂ネットワークモデル／連続体に亀裂を配したモデルなどを用いて取り扱う．処分領域に対する涵養域および処分領域からの流出域を含めた地下水の移行経路の全域に対して，単純な連続体モデルが適用できるような地質体はわが国にはほぼ存在しないと言える．わが国では（潜在的に）水みちとなりえる断層・節理などの構造が複雑に発達しており，水みちの異方性を考慮した移流・拡散現象の解析・評価が必要とされる．

断層などが境界となっている単一の水理地質ユニットと扱える領域内では，原位置および室内試験より直接測定された透水特性と物理探査より得られる物理物性の関係を評価し，物理探査により得られる各種物性値をそれぞれのモデルに対応したモデル定数に換算し，移流・拡散などの物質移行現象が解析･評価される．各種物性値は一般的に連続体モデルに基づく方法により整理されるが，亀裂を陽に捕らえるモデルが採用される場合にはこれに対応するモデル定数として整理される必要がある．以下，水理特性に関係する調査項目を示す．

①地下水の流向・流速，間隙水圧：ボーリング孔が掘削された水理地質ユニットあるいは境界となる断層などの地下水流動に関する実データ

②水文地質ユニットおよび主要断層の物質移行特性の代表値： 移流現象（透水係数，比貯留率，空隙率），拡散現象（拡散係数，遅延係数）

③各水文地質ユニットの物質移行特性と物理物性の関係：物理探査結果に基づき解析モデル内に物質移行特性を割り付ける際の基準

④水文地質ユニット内の地質体の性状変化に対する物質移行特性の変化：基質部については応力場の変化に伴う物質移行特性の変化，水文地質ユニットの境界にならない断層および亀裂については開口・閉塞に伴う物質移行特性の変化

⑤断層および亀裂の密度，開口幅，連結性：亀裂モデルを用いる際に必要となる物質移行に関するモデル定数

 

流向・流速および間隙水圧の原位置測定法

地下水の流向・流速の測定方法はその測定原理や手法の違いにより，地球化学的手法・物理的手法・水理学的手法・トレーサー法などに分類される（張ほか，2001）．それぞれの手法の概念および利欠点を表1-1に，総合的考察を以下に示す．間隙水圧の測定方法については表1-1中の水理学的手法と同様である．

①トレーサー法を除いた全ての測定手法は基本的に地下水の流向・流速の評価に適用できる．

②地球化学的手法と水収支平衡法は地下水の垂直流速の評価に適用し，その他の全ての手法・方法は地下水の水平方向の流向・流速の評価に適用できる．

③試験孔や観測孔を利用した測定方法は地表測定に比べ比較的深部までの調査が可能である．

④他の手法に比べ，地球化学的手法は比較的長時間の流向・流速の評価が可能である．言い換えれば，地球化学的手法以外の方法は流速の遅い地層での測定評価が基本的に困難である．

⑤処分深度における極めて遅い流速・流向を高精度，定量的に測定できる手法はない．

⑥表1-1で明確に示されていないが，亀裂や不連続面における流向・流速の測定技術はいまだ確立されていない状況にあると考えられる．

  • 表1-1　地下水流動の主な測定調査法

注：見方の違いによって異なった分類法が考えられる．また，コストの高低および調査範囲の広さについては他の手法との比較による定性的な表現である．

＊既存の井戸またはボーリング孔を利用できる場合では，コストが低くなる． 1) Allison & Hughes(1983), 2) ASTM(2006), 3)Barnes & Allison(1984), 4)伊藤ほか(1984), 5)小松田(1990), 6)西垣(1991), 7)Phillips et al.(1988), 8)佐倉(1984), 9)Sharma & Hughes(1985), 10)内田ほか(1993)

 

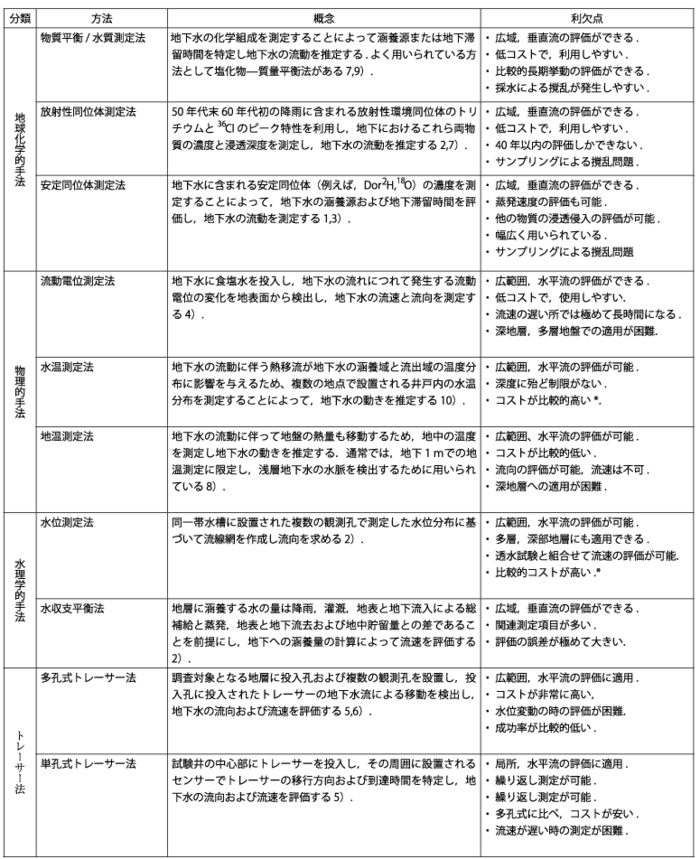
原位置透水試験法

原位置透水試験は室内透水試験と比較し，地層・岩体や断層などの透水性をその場で測定できるメリットがあり，また決定論的な評価が必要な極めて透水性の高い水みちとなる断層などを評価するための唯一の方法である．しかし，試験条件の制御がボーリング孔内の操作だけとなるため，境界条件の制御・特定や透水特性と直接関連する地圧・間隙水圧などとの関係を評価することは困難である．一方，室内透水試験では試験体の代表性を吟味する必要があるが，採取されたコアの地層中での存在状態，即ち，地圧・間隙水圧・低い動水勾配などを再現した状態で試験が可能であり，これら存在状態の変化（応力場の変化や異常間隙水圧の発生など）に応じた物質移行特性の変化を測定できる．また，室内透水試験では弾性波試験等とのカップリングも可能であり，これにより評価される透水特性−物理物性の関連性は数多く存在する透水性の比較的低い水みちによる地下水流動の寄与分を評価したり，物理探査・検層結果に基づく物理特性−透水特性の関連性を把握する上で重要なデータとなる．

原位置透水試験の代表的な試験法を測定孔数によって分類し，その概念と試験法の概略に表1-2に示す．各種原位置透水試験の概念図については関連文献を参照されたい（例えば地盤工学会，1980；1995；張ほか，2000；2001）

 

  • 表1-2　原位置透水試験法

 

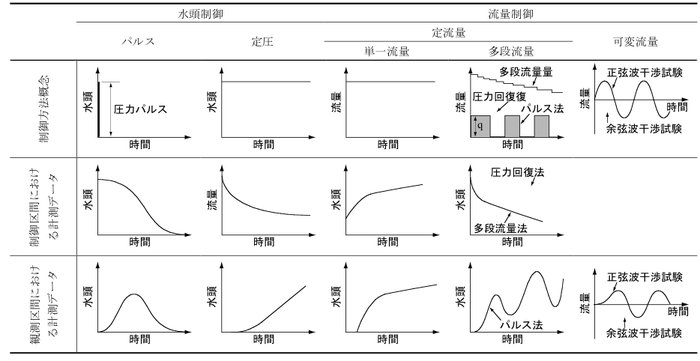
  • 表1-3　ルジオン試験における有効注水圧力（Peff）の計算

①ルジオン試験：ルジオン試験で求められる岩盤の水理学的バラメータは，岩盤の透水係数ではなく，岩盤の透水性の指標となるルジオン値である．この値は，試験区間内に10kgf/cm2(0.98MN/m2)の圧力で注水し，試験区間1m当たりの1分間の注水量と定義されている．そこで，有効注水圧力Peffの計算は地下水位と試験区間との相対的な位置関係によって表1-3に示す3種類に分けられる（例えば地盤工学会，1995）．

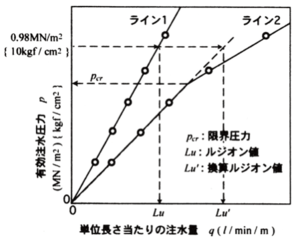
また，ルジオン値の決定方法は限界圧力の有無によって異なる．図1-1にルジオン試験結果からルジオン値の求め方の概略を示す．ここで，縦軸と横軸はそれぞれ有効注水圧力Peff (kgf/cm2)と単位長さ（1m）あたりの注水量q(l/min/m)である．

ルジオン値（Lu）は，図1-1に示されているライン1のようなPeff-q曲線に線形関係があることを確認した後，有効注入圧力10kgf/cm2時の注水量として求める．ルジオン値を透水係数に換算すると，1ルジオンは約1×10-5cm/sである．注水圧力を段階的に増加し試験を行う際，図1-1に示されているライン2のように，ある注水圧力以上になると注水量が急激に増大する場合では，このPeff-q直線関係が変わる点における有効注水圧力を限界圧力Pcrと定義される．この際，初段階のPeff-q曲線の限界圧力以下の直線を延長して有効注水圧力10kgf/cm2に相当する単位長さ当たりの注水量(l/min/m)を求めて換算ルジオン値（Lu’）とする（地盤工学会，1995）．
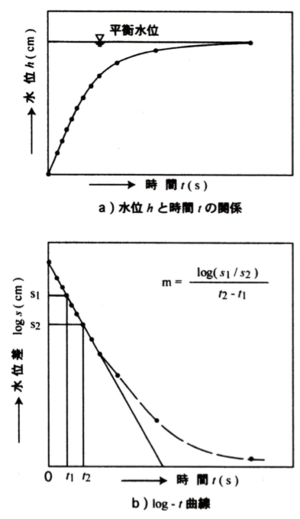
②J.F.T.法：図1-2にJ.F.T.法の実測結果から透水係数を求める手順を示す．図1-2 a)のような水位と時間の実測結果を図1-2 b)に示すように水位差と時間を片対数座標系に整理し，曲線の初期の直線部分の勾配(m)を求める．岩盤の平均透水係数K(cm/s)はボシュレフ(Hvorslev,1951)の理論式によって求められるが，岩盤自身の帯水状況及び試験区間の形状によって異なってくる．表1-4にJ.F.T.法における透水係数の算出方法をまとめる．
③定圧注水試験：岩盤の平均透水係数K(cm/s)は基本的にボシュレフ(Hvorslev,1951)の理論式によって求められるが，岩盤自身の帯水状況及び試験区間の形状によって異なってくる．表1-5に定圧注水試験法における透水係数の簡略算出方法をまとめる．

  • 図1-1 ルジオン値の算出方法（地盤工学会，1995）

  • 図1-2 J. F. T.法における透水係数の算出方法（地盤工学会，1995）

④スラグテスト：スラグテスト自身は調査対象となる地層の帯水状況や瞬時的に変化させた水頭の減衰特性の違いによって，試験のやり方や解析手法なども異なってくる．本稿では，被圧帯水層で，水頭の過減衰(Overdamped，水頭が単調に低下し，慣性力による周期的な振動が発生しない)状態の場合を例として簡単に紹介する．この場合，観測井に一定の水を急激に注入する．観測井に一定の水を急激に注入することによって，観測井内にH0の水頭を瞬時的増加させ，この瞬時的に増加させた水頭の経時的な変化を測定し，表1-6に示すCooper et al. (1967)の手法を用いて地層の透水係数および貯留係数を評価することができる．
⑤パルス透水試験：パルス試験結果の整理は比較的煩雑で，試験条件の違いによって異なってくる．表1-7にパルス試験結果の整理手法を示す．実際の整理にあたって，表1-7に定義されている無次元パラメータαは事前に分からないため，計算はまずα≦0.1と仮定し，Cooper et al.（1967）の手法より試算を行ってみる．その結果，もしα>0.1と判断された場合，改めてPapadopulos et al.(1973)の手法より計算し直す必要がある．
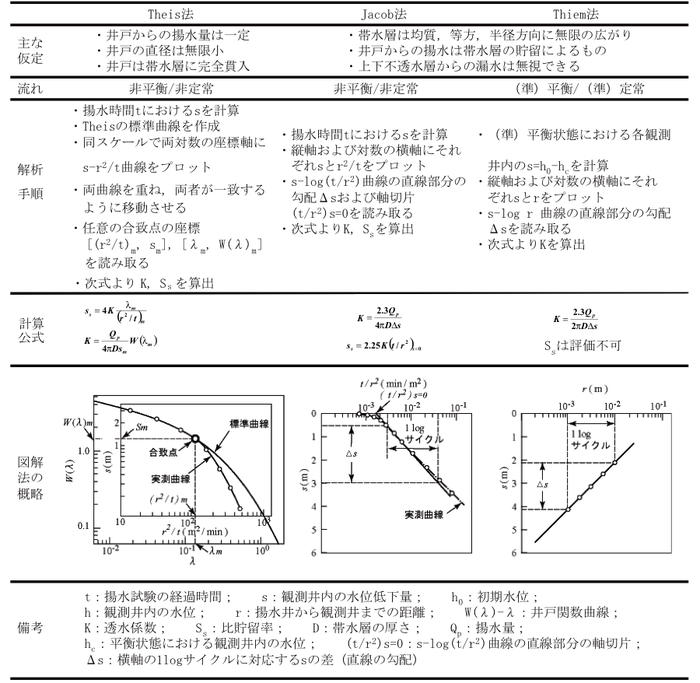
⑥揚水試験：揚水試験の解析は帯水層の地質条件，境界条件，揚水井の貫入状況，井戸貯留の有無および流れの状態などによって異なる．これらのうち最も一般的に用いられているのはTheis法，Cooper-Jacob法（Modified Theis Nonequilibrium Test Methodとも呼ばれる）およびThiem法である（地盤工学会，1995）．これら三つの解析法の主な仮定条件，解析手順および計算公式などの概要を表1-8にまとめる．
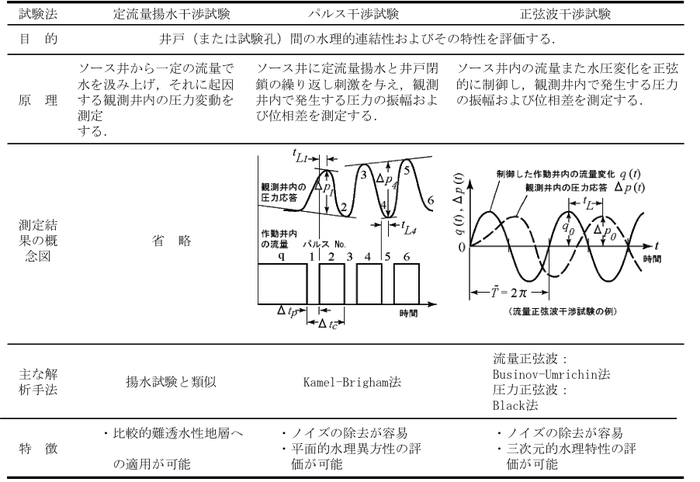
⑦干渉試験：干渉試験はソース信号の違いによって，主に定流量揚水干渉試験（注水の場合も類似），パルス干渉試験および正弦波干渉試験などに分けられる．表1-9にそれぞれの試験法の原理および主な解析手法をまとめる．

 

  • 表1-4　J.F.T.法における岩盤透水係数の算出方法

 

  • 表1-5　低圧注水試験における岩盤透水係数の簡略算出方法

 

  • 表1-6　スラグテストにおけるCooper et al.法

 

  • 表1-7　原位置パルス透水試験結果の整理手法

 

  • 表1-8　揚水試験におけるTheis法，Jacob法およびThiem法

 

  • 表1-9　原位置水理干渉試験の分類

 

原位置透水試験の解析手法

高レベル放射性廃棄物地層処分の安全性評価では，処分予定深度を含む広域的な地下水流動を把握することが不可欠である．このため，地下浅所から300m以深までの各層序の透水性を原位置透水試験等の手法により評価することが必要である．しかし，原位置透水試験に必要とされる掘削作業は岩盤の長期的遮蔽性能を損なう恐れもあり，掘削するボーリング孔の数は可能な限り最小限に抑えることが肝要である．ここでは，一本のボーリング孔を利用する代表的な単孔式透水試験法のパルス透水試験，定圧試験，定流量試験の解析手法に対して理論および数値解析の手法を用いて適用条件および評価精度の検討結果を示す．
パルス透水試験はパッカーで区切られた試験区間に対して瞬間的に圧力をかけ，その減衰を計測するものである．同法は難透水性層を対象とする場合でも比較的短時間で試験が実施でき，海外では難透水性層を対象とする試験法として基準化されている（例えば，ASTM 2002）．定圧試験では試験区間に一定圧で注水あるいは揚水し流量の経時的変化を計測し，定流量試験では試験区間に一定流量で注水または揚水し，試験区間内の圧力の変化を計測する（張ほか，2000；張ほか，2001）．それぞれの試験では，計測された試験区間内の圧力または流量のデータから解析解等により透水係数を評価する．代表的な解析解としては，地盤工学会の試験基準に採用されているHvorslevの定常解析モデルに基づくものとASTMにおいて採用されている放射流非定常モデルに基づくものが挙げられる（地盤工学会，1995；ASTM 2002）．これ以外にも，試験区間周囲のスキン（掘削，目詰まり等による孔井周囲の物性が変化した領域）や，亀裂性岩盤でのマトリックス部への透水等を考慮したものなど多様な解析モデルとそれらに基づく解析解がある（Hyder et al., 1994; Dougherty and Babu, 1984）．多くの解析モデルの開発と解析解が導出される一方で，その適用を検討するための明確な指針は確立されておらず，解析モデルの差異が透水係数の評価結果に及ぼす影響は検証されていない現状にある．また，実際の原位置試験では同一試験区間に対して幾つかの試験法を適用することがあるが（Martinez-Landa and Carrera, 2005），試験法毎に透水係数が異なった場合には有意な値を判断する必要が生じる．原位置透水試験の実施で直面するこれらの問題を検討するため，以下では，パルス透水試験，定圧試験，定流量試験の代表的な解析モデルの整理と新たに開発した解析モデルを用いて各解析モデルの適用条件と試験法間での差異を検証した．

 

解析モデル及び解析解

Hvorslevの解析モデルおよび放射流モデルの概念図を図1-3(a)および(b)に示す．Hvorslevの解析モデルは地盤工学会で採用されており，試験区間からの水頭ポテンシャル面は楕円体をなし，定常流れを仮定している（以下，HVモデル）（Hvorslev, 1951）．放射流非定常モデルはASTMで採用されており，地層の厚さは試験区間と同じとし，上下方向への流れは起きないと仮定している（以下，RFモデル）．新たに開発した解析モデルの概念図を図1-3(c)および(d)に示す．図1-3(c)に示す解析モデルでは試験対象となる地層の上下に不透水性層が存在すると仮定し，パッカーで閉鎖される試験区間は試験対象となる地層厚さの一部としている（以下，AF-ZFモデル）．この解析モデルに更にスキンの影響を考慮した解析モデルはこれまでにも開発されてきているが（Novakowski, 1993），スキンの特性値を特定する明確な方法はないため，ここではこれを除いたモデルを採用した．図1-3(d)に示す解析モデルはAF-ZFモデルとほぼ同様であるが，試験対象地層を低透水性とし，その上下に試験対象地層と比較し透水性が非常に大きい地層あるいは亀裂が存在し，それら内部での水頭消散は瞬時に終わると仮定している．これまでに，上下地層の透水性を考慮したモデルは開発されてきているが（Moench, 1985），それら解析モデルの適用には試験対象地層以外の上下地層の透水性評価が必要である．また，図1-3(c)および(d)で仮定するモデルは，試験対象地層と上下地層の透水性の差を考慮するモデルの両極にあたり，これらのモデルを用いた検証により試験対象地層と上下地層の透水性の差が小さな場合も検討が可能となる．表1-10に新たに開発した軸対称流非定常モデル（AF-ZF及びAF-CHモデル）の数学モデルと導出した解析解を示す．解析モデル間および試験法間での対比を行うため，表1-10に示す解析解は一律の無次元パラメータで整理した．HVモデルおよびRFモデルから得られる解析解も同一の無次元パラメータにより再整理した(表1-11)．なお，パルス透水試験及び定流量透水試験の無次元数学モデルには試験対象となる地層と試験区間の貯留特性を反映する無次元パラメータβが含まれているが，透水性が比較的低い岩盤を対象とする場合には10-1〜101程度の値となると想定される（Pickens et al., 1987; Bredehoeft and Papadopulos, 1980）．以下の解析解を用いた数値シミュレーションでは，試験条件を代表するパラメータはζL=102およびζB=5×102，試験区間は試験対象地層の中間に位置するとし，貯留性を代表するパラメータはβ=10-2〜102，透水性は等方（α=100）とした．

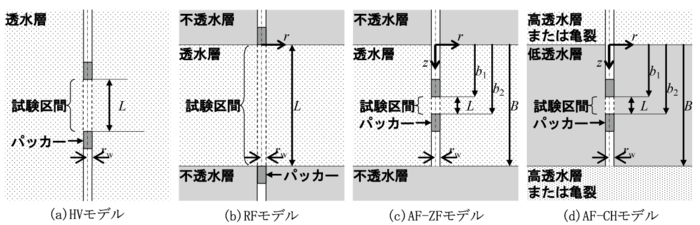
  • 図1-3 単孔式原位置透水試験の概念と解析モデル．

①パルス透水試験

図1-3に示した各解析モデルの差異を検証するために，パルス透水試験の計測データにあたる試験区間での水頭変化を各モデルの解析解を用い算出した（図1-4）．図中，非定常流れを仮定するRF，AF-ZF及びAF-CHモデルから算出された水頭変化を示す曲線はほぼ一致した．一方，定常流れを仮定するHVモデルは非定常流れを仮定するモデルとは合致せず，βの値が小さい場合にその差は大きくなる傾向にある．これらの結果より，RF，AF-ZF及びAF-CHモデルから決定される透水係数および比貯留率に大きな差は生じないと考えられる．

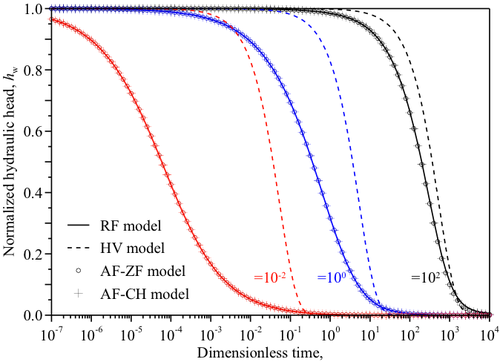
  • 図1-4　解析モデルによるパルス透水試験の試験区間水頭の計算結果の違い．

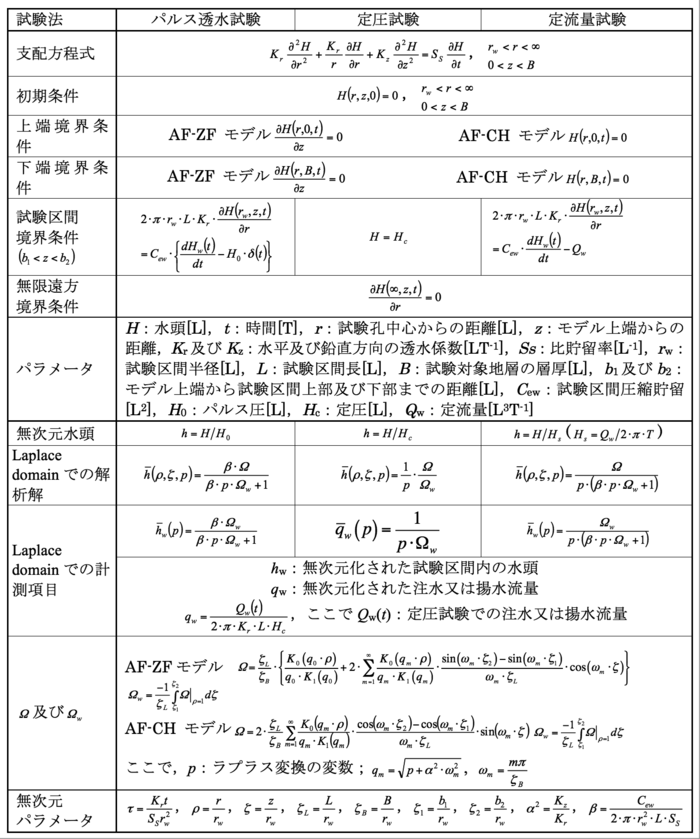
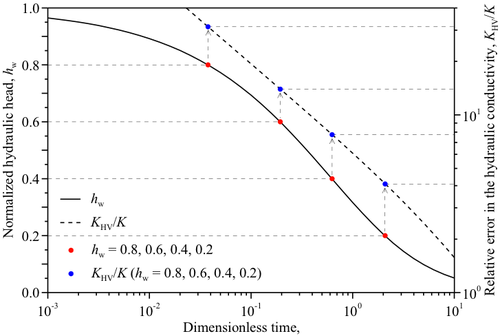
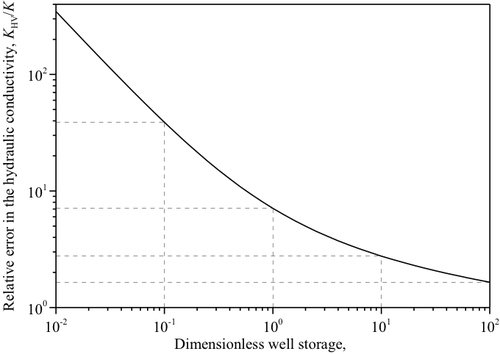
HVモデルと他のモデルでパルス透水試験を評価した場合の透水係数の差を検証するために，RFモデルにより算出した水頭変化からHVモデルを用い透水係数の算出を行った．β=10-1の条件下でのHVモデルによる透水係数の相対誤差を図1-5 (a)に示す．図中，試験区間水頭hw=0.8，0.6，0.4，0.2の値に対応する相対誤差はおよそ30〜4倍の範囲にあり，HVモデルにより算出される透水係数は水頭値hwに依存することが分かる．このため，HVモデルによりスラグ透水試験を評価する際には，試験区間水頭hwが0.37前後の計測データから透水係数を算出することが推奨されており，タイムラグ法として広く用いられている(Butler, 1997)．このタイムラグ法のパルス透水試験への適用性を検証するため，β=10-2〜102の範囲でhw=0.37となる時刻をRFモデルにより算出し，HVモデルによる透水係数の評価を行った（図1-5 (b)）．その結果，パルス透水試験で想定されるβ=10-1〜101の範囲では，透水係数は大きく評価され，βの値が小さい場合には数十倍と過大評価される可能性が明らかとなった．これらの結果からパルス透水試験において透水係数の評価を行う際には，計測データ全てに対してフィッティングを行うことが適していると考えられる．ただし，計測データである試験区間水頭hwは透水係数および比貯留率について非線形となるため（表1-10および表1-11），ASTMの試験基準で規定される試験区間水頭hwの標準曲線群を用いる図解法や逆解析による試験評価が必要となる．ここでは逆解析による試験評価の適用性を検証するために，以下の式を用いて試験区間水頭に対する透水係数および比貯留率の感度係数をRF，AF-ZF及びAF-CHモデルにより評価した．

\frac{K}{H_0}\cdot\frac{\partial H_w}{\partial K} = \tau \cdot \frac{\partial h_w}{\partial \tau} (1）

\frac{Ss}{H_0}\cdot \frac{\partial H_w}{\partial Ss} =-\biggl(\tau \cdot \frac{\partial h_w}{\partial \tau} + \beta \cdot \frac{\partial h_w}{\partial \beta}\biggl) （2）

 

  • 表1-10　 AF-ZFおよびAF-CHモデルの数学モデルおよび解析解．

 

  • 表1-11　 HVおよびRFモデルより得られる各試験法の無次元解析解．

各解析モデルより算出された感度係数はほぼ同じ値となった．このことより逆解析に異なる非定常解析モデルを適用しても評価結果に顕著な差は生じないと考えられる．例として，図1-6にAF-CHモデルより算出した感度係数を示す．β=10-2では透水係数および比貯留率の感度係数はほぼ同じとなり，βの値が大きくなるほど透水係数に対する感度係数は大きくなり，比貯留率に対する感度係数は小さくなる傾向にある．β=10-2〜102の範囲での透水係数および比貯留率の感度係数は同じオーダーにあることが確認できるが，図1-4に示すようにβが小さい場合（例えば，β=10-2と100）の試験区間の水頭変化の傾向はほとんど同じとなるため，βに含まれる比貯留率の評価精度はPapadopulos et al.（1973）が指摘しているように悪くなる可能性がある．

  • 図1-5(a)　パルス透水試験のHVモデルによる試験評価で透水係数に生じる誤差．

  • 図1-5(b)　パルス透水試験のHVモデルによる試験評価で透水係数に生じる誤差．

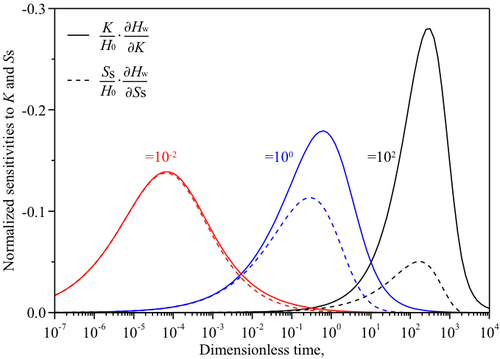
  • 図1-6　パルス透水試験における透水係数K及び比貯留率Ssの感度．

②定圧試験

図1-7に各解析モデルから算出した定圧試験の計測データにあたる試験区間での流量の経時的変化を示す．非定常流れを仮定するRF，AF-ZF及びAF-CHモデルは流量が大きく変化する試験初期段階においてほぼ同じ値となった．一方，定常状態に近づくと，AF-ZF及びAF-CHモデルから算出された流量はRFモデルから算出された流量と乖離し，定常流れを仮定するHVモデルから算出された値に近くなる．これらより，非定常状態の計測データを解析する場合には，通常のRFモデルを用いてもAF-ZF及びAF-CHモデルと同様の透水係数及び比貯留率の値が得られると考えられる．また，定常状態の流量からHVモデルを用いて透水係数を算出してもAF-ZFおよびAF-CHモデルとほぼ同じ透水係数の値が得られると考えられる．

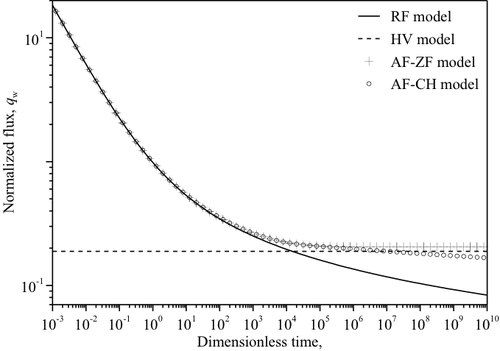
  • 図1-7　解析モデルによる定圧試験の試験区間流量の計算結果の違い．

試験対象地層の上下を不透水性層または透水性の高い層が挟む場合にHVモデルを用いた試験評価で透水係数に生じる誤差を検証した．図1-8にAF-ZF及びAF-CHモデルより算出した流量を“計測データ”として扱いHVモデルにより算出した透水係数を示す．これらの結果から定常状態における流量からHVモデルを用いて透水係数を算出してもその相対誤差は数パーセント程度となることが考えられる．ただし，試験対象地層の層厚（ζB）が試験区間長（ζL）と比較し小さくなる場合や鉛直方向の透水係数が大きくなる場合（α>1）には相対誤差が大きくなると考えられる．

非定常計測データから逆解析により透水係数及び比貯留率を求める場合を想定し，AF-ZF及びAF-CHモデルから透水係数及び比貯留率の感度係数を次式により算出した（図1-9）．

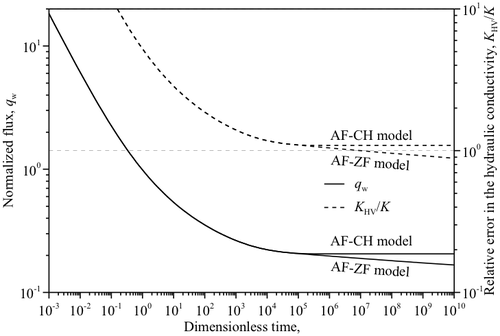
  • 図1-8　定圧試験のHVモデルによる試験評価で透水係数に生じる誤差．

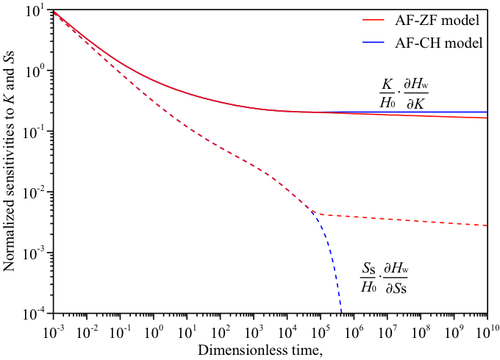
  • 図1-9 定圧試験における透水係数K及び比貯留率Ssへの感度．

\frac{K}{Q_s} \cdot \frac{\partial Q_w}{\partial K} = q_w + \tau \cdot \frac{\partial q_w}{\partial \tau} （3）

\frac{Ss}{Q_s} \cdot \frac{\partial Q_w}{\partial Ss} = -\tau \cdot \frac{\partial q_w}{\partial \tau} （4）

AF-ZF及びAF-CHモデルより得られた結果では，比貯留率に対する感度係数は透水係数に対する感度係数と比較し小さく，定常状態に近づくと１オーダー以上小さな値となる．また，AF-CHモデルの比貯留率に対する感度係数は定常状態に達すると無限小の値となる．これらより，非定常状態のデータ数が定常状態のデータ数と比較して少ない場合に，逆解析で決定される比貯留率の評価誤差は透水係数と比較し大きくなりやすいと考えられる．
③定流量試験

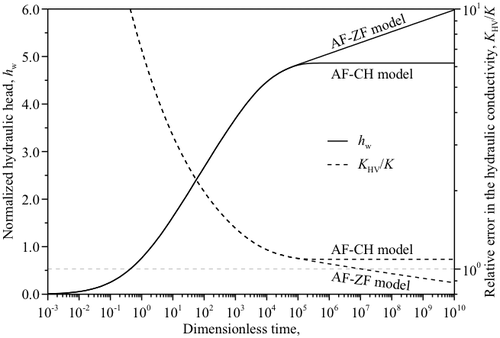
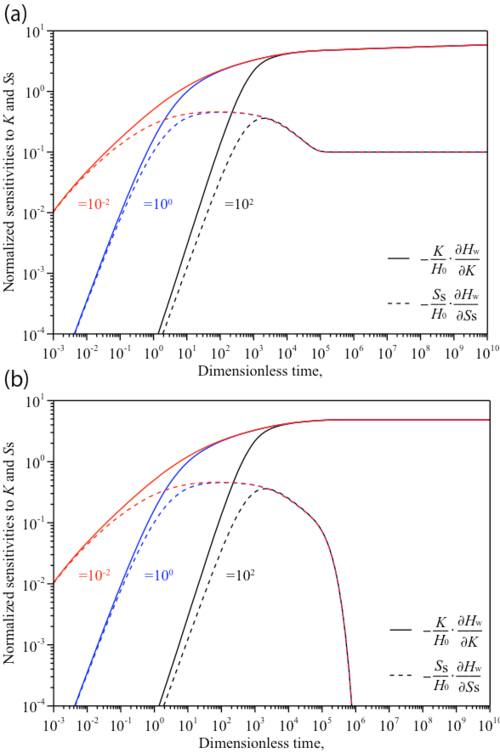
各解析モデルから算出した定流量試験の計測データにあたる試験区間での水頭の経時的変化を図1-10に示す．非定常流れを仮定するRF，AF-ZF及びAF-CHモデルから算出した試験区間水頭は試験初期段階においてほぼ同じ値となった．しかし，βの値が小さくなるほどRFモデルから算出した試験区間水頭はAF-ZF及びAF-CHモデルから算出したものからより早く乖離する傾向にある．一方，定常流れを仮定するHVモデルから算出された試験区間水頭はAF-ZF及びAF-CHモデルから算出したもとの定常状態において近い値となるものの同一の値とはならない．しかし，その相対誤差は図1-10中では10％程度であり，HVモデルが定流量試験においても予備的な透水係数評価に適用できる可能性が示唆される．これを検討するために，AF-ZF及びAF-CHモデルから算出した試験区間水頭を“計測データ”とみなしHVモデルを用いて透水係数を算出した結果，HVモデルによって算出される透水係数は定常状態に達した後の試験区間水頭を用いると数％程度となった（図1-11）．ただし，AF-ZF及びAF-CHモデルから算出される試験区間水頭は試験対象地層の層厚（ζB）と試験区間長（ζL）の大小関係，透水異方性（α）にも依存するため，HVモデルにより算出された透水係数は参照値として扱う必要があると考えられる．従って，定流量試験においてもパルス透水試験および定圧試験と同様，非定常計測データを用いる図解法または逆解析による透水係数および比貯留率の評価が必要である．このため試験区間水頭の透水係数および比貯留率に対する感度をAF-ZF及びAF-CHモデルを用い次式により算出した（図1-12）．

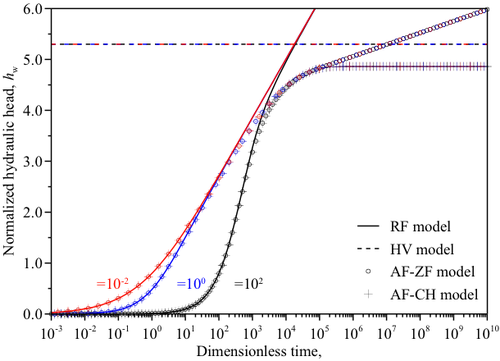
  • 図1-10　解析モデルによる定流量試験の試験区間水頭の計算結果の違い．

  • 図1-11　定流量試験のHVモデルによる試験評価で透水係数に生じる誤差．

  • 図1-12 定流量試験における透水係数K及び比貯留率Ssへの感度．

 

\frac{K}{H_s} \cdot \frac{\partial H_w}{\partial K} = -h_w + \tau \cdot \frac{\partial h_w}{\partial \tau} （5）

\frac{Ss}{H_s} \cdot \frac{\partial H_w}{\partial Ss} = -\biggl(\tau \cdot \frac{\partial h_w}{\partial \tau} +\beta \cdot \frac{\partial h_w}{\partial \beta}\biggl) （6）

図1-12(a)および(b)において透水係数に対する感度係数はAF-ZF及びAF-CHモデルともに比貯留率に対する感度係数と比較して大きく，定常状態においては定圧試験と同様1オーダー以上大きくなった．このことから定圧試験同様，定常状態の試験区間水頭を多く含む計測データを逆解析に用いると比貯留率の評価誤差は大きくなることが考えられる．特に，試験対象地層が上下に透水性の高い地層で挟まれる場合（AF-CHモデル）には比貯留率の影響は非定常状態の試験区間水頭のみに含まれると考えられる．

 

単孔式透水試験の理論的検討による知見

原位置単孔式透水試験のパルス透水試験，定圧試験，定流量試験の代表的な解析モデルを一律の無次元パラメータで再整理するとともに，試験対象地層の上下の水理地質境界を考慮した新たな解析モデルの開発と解析解の導出を行い，各モデルを対比した数値シミュレーションを実施した．その結果，以下の知見が得られた．

  • 各解析モデルの適用性は試験方法によって異なることが明らかとなった．特に，パルス透水試験では，HVモデルの適用により透水係数が過大評価される可能性があり，その程度は地層と試験区間の貯留特性の比(β)に依存することが明らかとなった．
  • RFモデルは非定常状態初期の計測データに適用可能と考えられるが，定流量試験においてはβの値に依存することが明らかとなった．
  • HVモデルによる透水係数の評価は計測データが定常状態となりうる定圧試験や定流量試験において可能と考えられるが，試験対象地層の層厚（ζB）と試験区間長（ζL）の大小関係，透水異方性（α）に依存すると考えられる．このためHVモデルにより得られた結果はより精緻な解析モデルを用いて試験評価を行う際の参考とすべきである．
  • 以上の検討で用いた解析モデルは地層を均質な連続体と仮定したものであり，実際の原位置地層とは乖離している場合も想定される．実際の試験では試験孔周囲のスキン，亀裂性岩盤でのマトリックス部への透水，軸対称モデルでは再現不可能な亀裂等が透水試験に影響する可能性も想定される．従って，これらの影響についても簡易に検討するための知見の整備が必要と考えられる．

岩石の移流拡散特性の評価技術

| ↑ top | 採水法 | 現位置調査 | 岩石の移流拡散特性 |

高レベル放射性廃棄物の地層処分を安全に実施及び評価するためには，多くの特質・事象及びプロセス（FEPs）を考慮する必要があるが（OECD/NEA，2000），地球科学分野における重要課題は，主に変動シナリオ及び地下水移行シナリオに基づく天然バリアの長期的安定性，もしくは長期的隔離性能の評価に分けることが可能である（鹿園，1995）．後者の地下水移行シナリオに基づく地層処分施設の長期的安全性評価は基本的に多重バリアシステムにおける核種移行解析及び感度解析などより実施されるが，安全評価の精度及び信頼性を確保するためには，評価に利用される数理モデルが評価対象となるバリアシステムを適切に記述・モデリングできること，解析に入力する各パラメータの値は評価対象の物性を代表できること，さらに長期にわたる物性の変化を適切に考慮・評価できることなどが必要不可欠である．

天然バリア，すなわち母岩もしくは岩盤における核種の移行は一般の化学物質と同様に，移流，分散，吸着，崩壊及び化学平衡などの現象に支配される（例えば，張・竹田，2004）．母岩が比較的均質な堆積岩の場合，移流・分散によって，核種の濃度が希釈され，吸着によって地下深部にトラップされる．核種の崩壊は連鎖的であり，崩壊により親核種の濃度が減少するが，娘核種の濃度は増加傾向になる．また，化学反応を伴う吸着現象は天然バリアの遅延効果を考慮する上で非常に重要な要素ではある．母岩が結晶質岩である場合，亀裂の進展方向に沿った移流が支配的となるが，亀裂に直交した方向における浸透と拡散は，吸着作用と同様に天然バリアの遅延効果に大きく寄与する（Zhang, 2009）．また，地層処分の対象となる地下深部においては，動水勾配が極めて小さく，分散現象は拡散現象に等しくなる．ここでは，岩盤内移流拡散特性の変遷要因，移流拡散評価技術とその他物性との関連性，透水及び拡散試験支配方程式の相似性などを概説し，室内における岩石を対象とする透水試験と拡散試験に関する研究成果を示す．

 

岩盤の移流拡散特性の変遷要因

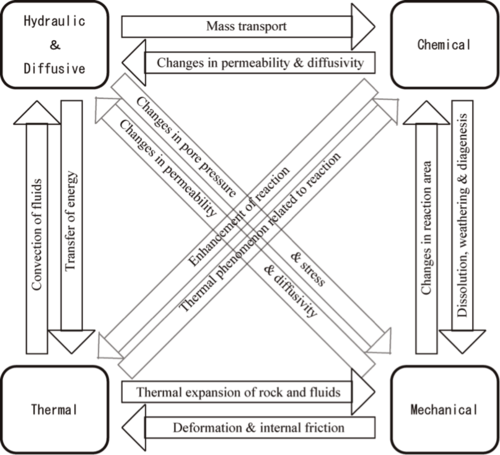
岩盤における地下水の流速は地層の透水係数，動水勾配及び有効空隙率に依存する．また，核種の移行は実効拡散係数に依存する．高レベル放射性廃棄物地層処分施設の長期的安全性もしくは性能評価を行う際には，これら物性の変動要因を考慮する必要がある．これは10万年以上にも及ぶ長期間の間に，地層における熱的，力学的及び化学的な変化が地層の移流拡散特性に影響することが考えられるためである（図1-13）（例えば，張・竹田，2004）．

  • 図1-13　熱力学的，力学的及び化学的要因が岩石の移流拡散特性に及ぼす影響．

地層における化学的変化はその移流拡散特性を変化させ，逆に地下水の流動に伴う物質の移行は連鎖的に化学反応を引き起すこともある．例えば，鉱物の沈澱・結晶化は岩盤の空隙に生成鉱物を充填し，透水及び拡散性能を低下させ，天然バリアとしての隔離性能を上昇させることになるが，地下水の流動は化学平衡を崩し，これに起因する鉱物の溶解は逆に岩盤の空隙率を増加させ，沈澱と相反の効果が生じることになる．

地層の力学的特性変化，もしくは地層の変形は地層の透水及び拡散特性を変化させ，逆に地下水の存在と流動や異常塩濃度の増加などは間隙水圧及び有効応力の変化を引き起し，地層の力学的特性に影響を与える．例えば，地層の圧縮，圧密は地層の空隙率を減少させ，透水係数及び有効拡散係数の低下や，場合によっては異常水圧も引き起こす．逆に，地層変形に伴うダイラタンシーや岩盤の破壊は地層の透水性を増加させ，場合によっては流体の流れ道となる亀裂や断層なども生じさせる．
地層における熱的変化は間隙流体の対流などを引き起こし，移流拡散特性に影響を与える．逆に，地下流体の流動に伴うエネルギーの伝播は地層中の温度勾配を変化させ，地層の熱的特性に影響を与える．

以上の移流拡散特性に対する化学的，力学的及び熱的状態の影響事象を紹介したが，同様に，それぞれの特性間にも直接的あるいは間接的に相互作用がある．例えば，地下水の流動に伴う熱エネルギーの伝播は，前述の対流を引き起すだけでなく，地層における温度勾配の変化により，化学反応にも影響を及ぼす．また，岩盤や間隙流体の熱膨張によって岩盤の力学的特性も変化する．これらの化学反応への影響と地層の力学的特性の変化は最終的に地層の移流拡散特性を変化させる．

このように，岩盤中の物質移行を支配する移流拡散特性は多くの要因に影響を受ける．高レベル放射性廃棄物地層処分施設の長期的安全性を評価するためには，様々な変化要因を考慮した信頼性の高い移流拡散特性の物性データを蓄積していく必要があると考えられる．

 

移流拡散評価技術とその他物性との関連性

岩石の移流拡散特性，すなわち透水及び拡散特性はそれぞれ透水及び拡散試験によって評価される．透水試験も拡散試験も，大別して室内試験及び原位置試験に分類することができる．前者は原位置から採取してきた試料を室内に持ち込んで試験を行うもので，後者は原位置の地層を「不撹乱状態」で試験することを意味する．室内試験は原位置試験に比べ，試験条件の制御が行いやすく，また試験費用も比較的安いため広く用いられているが，室内試験の試験体は現場の再現性や原位置地層の代表性などに問題があると指摘されている．しかし，試験条件を人為的に設定・変化させることが可能であるため，様々な変動要因を考慮した移流拡散特性の変化予測に必要な実験データの取得と知見整備などに利用することが可能であると考えられる．原位置試験は室内試験に比べ，境界条件などを正確に特定することが困難であるが，試験体を乱さない点からも，室内試験より優れている．また，地層に比較的大きなインパクトを与えられるため，地層の平均的な特性を求めることができ，原位置試験より得られる試験結果は実際の設計に利用されやすい（張ほか，2000; 2001b）．なお，原位置試験より得られる各種特性値は，その調査地点及び調査時点での岩盤物性値であり，放射性廃棄物地層処分施設などの長期的安全性評価においては関連物性値の時間的変化に伴う変化を考慮する必要もあることに注意されたい．

拡散試験は透水試験に比べ，試験に必要な時間が長く，また化学物質濃度のインライン測定・分析技術の限界により，深部地下の高い間隙水圧を再現した条件下での拡散試験は現状では不可能に近い．このため，地圧を再現した極一部の研究事例を除き(Van Loon et al., 2003; Skagius and Neretnieks, 1986; Drew and Vandergraaf, 1989)，殆どの拡散試験は応力条件を考慮せず，大気圧条件下で行ってきているのが現状である(Zhang, 2009; Zhang et al., 2005)．このため，岩石の透水係数と空隙率，実効拡散係数と空隙率，地圧と空隙率の相互関係を用い，地下深部応力条件下における岩石の実効拡散係数の推測方法が提案されている（Zhang, 2008）．

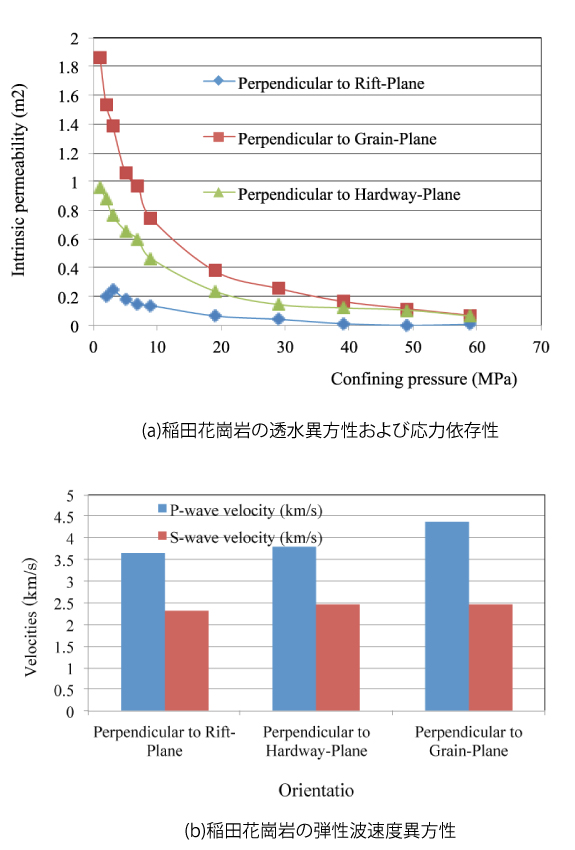
岩盤は一般的に非均質性及び異方性を持っているが，岩盤の移流及び拡散特性の空間分布及び異方性のすべてを直接透水及び拡散試験より求めるには多大な労力とコストを要する．代替的な評価方法として，岩石の移流拡散特性と弾性波速度などの物性と相関性が利用できると考えられる．岩盤の有効空隙率が大きいほど，密度は小さく，弾性波速度も小さく，透水及び実効拡散係数は大きくなる．図1-14に稲田花崗岩の透水係数の異方性および弾性波速度との相関性を示す．この図より，稲田花崗岩内部での弾性波伝播速度と透水係数の何れもRift, Hardway及びGrain面に直交した方向の順で大きくなる．すなわち，核種は相対的に有効空隙の大きい地層及び音波速度の比較的遅い方向に直交した方向において選択的に通ることになる (例えば，Zhang and Takeda, 2003)．

  • 図1-14 稲田花崗岩の透水係数の異方性および弾性波速度との相関性． →画像を拡大

 

室内における透水・拡散試験法

室内における透水・拡散試験法には，それぞれの試験原理とそれを数学的にモデル化した試験理論が対であり，計測データは試験理論から導かれた解析解を用いて解析され，各種物質移行特性が評価される．従って，実際の実験においてその試験原理とかけ離れた状態で行われた実験計測データに対して試験原理を忠実に再現する解析解を適用しても，得られる物性値は真の値と大きくかけ離れた値となることがある．実際にある特定の地層やサンプルコアの物質移行特性の評価を試みる際には，おおよそ予想される物質移行特性に応じた試験方法を選択し，その試験原理に忠実に試験を実施しなくてはならない．

各種室内または原位置試験の計測データから物質移行特性値を算出するための方法として主に解析法，図解法及び数値解析（逆解析）法等が挙げられる．また，定常状態の計測データから透水試験では透水係数，拡散試験では実効拡散係数，非定常状態の計測データから透水試験では透水係数及び比貯留率，拡散試験では実効拡散係数及び遅延係数が評価される．

  • 解析法は各種試験の解析解を適切に変換し，試験の計測データから直接透水係数あるいは実行拡散係数を算出する方法である．また，理論解の定常状態の部分に対して線形近似し，前述の方法により算出した透水係数あるいは実効拡散係数の値を用いて，比貯留率あるいは遅延係数を算出するタイムラグ法もある．この方法は基本的に定常状態の計測データにしか適用できない．
  • 図解法は各種試験の理論解を用い，必要な特性値を特定するための標準曲線を作成し，実測された計測データと標準曲線とを比較することによって各種特性値を決定する方法である．この方法は非定常状態の計測データに対して適用可能であるが，比貯留率あるいは遅延係数など非定常状態に関係する物性値が小さい場合にはこれら物性値の評価結果にオーダーに及ぶ誤差を生じる可能性がある．
  • 数値解析に基づく逆解析法は各種試験の厳密解または数値解を用い，解析結果と実測結果で定義される目的関数を最小化する手法で「最適な」パラメータの値を決定する．試験法によってはその厳密解中の特定されるパラメータ間に相関がある場合があるため，適用する際には事前にこれを把握しておく必要がある．

 

室内透水試験

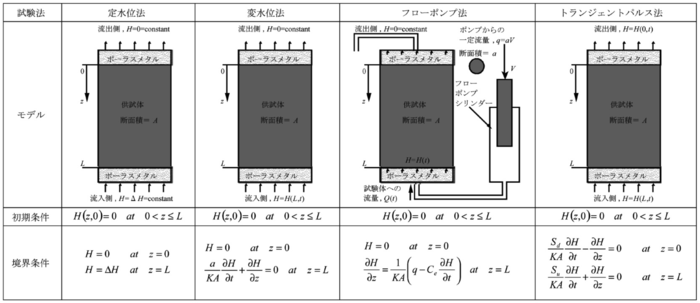
室内透水試験では採取されたコアの地層中での存在状態，即ち，地圧・間隙水圧・低い動水勾配などを再現した状態で試験が行われることが望ましい．室内透水試験は基本的に，流量計測に基づいて透水係数を求める定水位法及び変水位法（地盤工学会，1980），差圧力（水頭差）計測に基づいて透水係数を求めるフローポンプ法（定微流量法）（Olsen，1965；Olsen et al.,1985；Song et al., 2004）及びトランジェントパルス法（Brace et al.，1968），試験体の一端で間隙圧に一定周波数の振動を与え，他端の間隙圧の振幅の減衰率および遅れを計測し透水係数を求める間隙圧オシレーション法（Kranz et al.,1990）がある．これらの試験法のうちフローポンプ法を除く方法では試験開始直後に試験体上流端面付近に極めて大きな動水勾配（理論上無限大）が発生することが明らかとなっており（Zhang et al., 1998; 2000a; 2000b; 2002），前述の低い動水勾配下での試験を行えるのはフローポンプ法だけである．

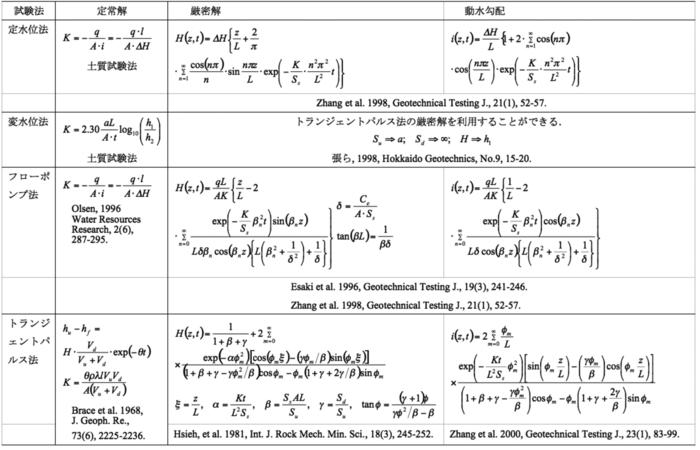
表1-12に各種室内透水試験法の概念図および解析モデル，試験の初期条件および境界条件を示す（張ほか，1997；高橋ほか，1998）．それぞれの室内透水試験の初期条件，境界条件及び次式（7）で表される飽和浸透流の一次元基礎方程式を用いると，表1-13に示す各種室内透水試験の厳密解が導かれる（Zhang et al.，2002）．

 

  • 表1-12　各種室内透水試験法の概念図および解析モデル

 

  • 表1-13　各種室内透水試験の厳密解

 

\frac{\partial^2 H}{\partial z^2}- \frac{Ss}{K} \cdot \frac{\partial H}{\partial t} = 0 (7)

ここで，H：供試体中の水圧（水頭）；Z：供試体の下流端面からの距離；K，Ss：それぞれ供試体の透水係数及び比貯留率；t ：実験開始後の経過時間である．

①定水位法：定常状態の流量測定結果を用い，表1-13に示す定水位法の定常解より供試体の透水係数を算出することができる．

②変水位法：準定常状態の水位変化測定結果を用い，表1-13に示す変水位法の定常解より供試体の透水係数を算出することができる．また，変水位透水試験をトランジェントパルス透水試験の特例として考えられるため，非定常状態の測定結果を用い，トランジェントパルス法の厳密解を利用すれば，供試体の透水係数及び比貯留率の両方を求めることも可能である（張ほか，1998）．

③フローポンプ法：定常状態の測定結果を用い，表1-13に示すフローポンプ法の定常解より供試体の透水係数を算出することができる．また，非定常状態の測定結果を用い，同表に示されているフローポンプ法の厳密解を利用すれば，逆解析法より供試体の透水係数のみならず，比貯留率をも同時に求められる．更に，非定常解析を用いることにより，難透水性材料の透水試験に必要な時間を大幅に短縮することも可能である（Esaki et al. 1996; Zhang et al., 1997）．

④トランジェントパルス法：準定常状態の測定結果および表1-13に示すトランジェントパルス法の定常解を用い，図解法より供試体の透水係数を算出することが可能である（Brace et al.，1968）．また，非定常状態の測定結果を用い，同表に示されているトランジェントパルス法の厳密解を利用すれば，図解法（Hsieh et al.，1981；Neuzil et al.，1981）もしくは逆解析法（Zhang et al.，2000b）より供試体の透水係数のみならず，比貯留率をも同時に評価することが可能である．

⑤間隙圧オシレーション法：定常解により算出される振幅の減衰率と位相の遅れに関する標準曲線を透水係数および比貯留率に関する無次元パラメータについて作成し，図解法により試験評価を行う（Fischer，1992）．また，定常解より導かれる減衰率と位相の遅れに関する２つの式にそれら実測値を代入し，透水係数および比貯留率を数値解析により特定することも可能である（高橋ほか，2003）．

室内拡散試験

室内拡散試験法は多数存在するが，ここでは室内拡散試験を透過拡散法，浸入拡散法（in-diffusion），浸出拡散法（out-diffusion），コラム法に大別する（張・竹田，2004; Zhang et al., 2006a）．
①透過拡散法

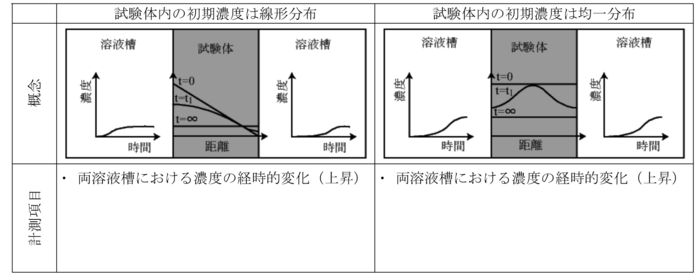
透過拡散法の試験原理は試験体を２つの溶液槽で挟み，一方の溶液槽にトレーサーを投入し，片方あるいは両方の溶液槽のトレーサー濃度を経時的に計測し，実効拡散係数および遅延係数を測定するものである．透過拡散法は表1-14に示すようにさらに４つの方法に分類される．

 

  • 表1-14　透過型室内拡散試験の試験方法

 

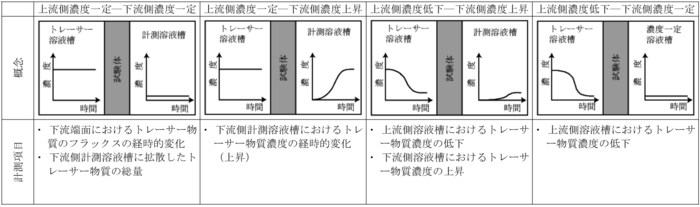
定濃度浸入−定濃度浸出法（constant inlet concentration-constant outlet concentration）：

この方法では両方の溶液槽の濃度差を一定に保ち，定濃度溶液槽側に透過してくるトレーサーの総量を経時的に計測する方法である．計測データのうち時間−透過総量曲線の定常状態の傾きから実効拡散係数を算出し，遅延係数は透過総量に対する理論解の定常状態の部分の線形近似式を用いタイムラグ法により算出する．試験評価には定常状態の計測データを用いるため，試験体の物質移行特性によっては試験に長時間を要する．この方法は，ベントナイト，ベントナイト混合土，コンクリート，岩石等，地層処分に関連する人工材料，地質媒体に対する試験で広く利用されている（例えば，Skagius and Neretnieks, 1986；Rebour et al., 1997；Sato et al., 1997；Tits et al., 2003）．しかし，この方法から求められる遅延係数は，岩石パウダーを対象とするバッチ試験と比較し３オーダー程度小さな値として見積もられることも珍しくなく，空隙率より小さな値で評価されることもある．
この問題点は試験の解析理論と実際の実験での操作の矛盾点，タイムラグ法によるデータ解析段階での誤差の発生などに起因することが明らかとなっている（Zhang and Takeda， 2005）．また，多くの実施例では濃度計測の容易さからトレーサー濃度を異常に高く設定する傾向が見られ，定濃度側のトレーサーの透過総量を計測するために，濃度を限りなく０に保ち，濃度検出ができる程度の透過量で溶液全てを濃度０の水と置換する作業を継続して行わなくてはならない．
定濃度浸入−浸出濃度増加法（constant inlet concentration-increasing outlet concentration）：

一方の溶液槽を定濃度に保ち，トレーサーが透過してくる溶液槽の濃度増加を経時的に計測する方法である．Rebour et al.（1997）を除きこの方法により透過拡散試験が実施された例はないが，前述の定濃度浸入−定濃度浸出法と比べ，試験管理が容易であり，試験手順に起因する計測誤差が低減されると考えられる．試験評価は非定常状態の計測データに対して行わなくてはならないため，Rebour et al.（1997）は数値解による試験評価を行っている．これに対し，Zhang and Takeda (2005)は試験評価の精度を向上させるために数値解にかわる解析解を導出している．しかしながら，この方法も定濃度浸入−定濃度浸出法と同様に，トレーサーが定濃度側に透過してくるまでに時間を要する．
浸入濃度減少−浸出濃度増加法（decreasing inlet concentration-increasing outlet concentration）：

この方法では一方の溶液槽にトレーサーを投入し，両方のトレーサー濃度の経時的変化を計測する．Garcia et al. (2004)はこの試験法の評価のために数値解を用いたが，Takeda et al.（2008b）は数値解による誤差を低減するために解析解を導出し，岩石コアを対象とした試験の評価にこの解析解を適用している．この試験法の利点は，溶液槽内の溶液を置換する必要がなく，適切に試験条件を設定するとトレーサー投入側の濃度低下が早くなり，また，解析解を用いることにより非定常状態の計測データに対しても試験評価が行え，試験時間を短くできる点にある．
浸入濃度増加−定濃度浸出法（decreasing inlet concentration-constant outlet concentration through-diffusion）：

この試験法は一方の溶液槽に一定量のトレーサーを投入し，他方の溶液槽内の溶液を常に置換することにより定濃度に保つ方法である．計測はトレーサー投入側の溶液槽内の濃度の経時的な変化である．この手法はトレーサー投入槽側の濃度計測をするため，定濃度浸入−定濃度浸出法と定濃度浸入−浸出濃度増加法と比較し試験時間が早く，定濃度浸入−定濃度浸出法より試験管理が容易である．この方法に対する解析解はZhang and Takeda (2005)により導出されているが，未だ適用例はない．
②浸入拡散法（In-diffusion method）

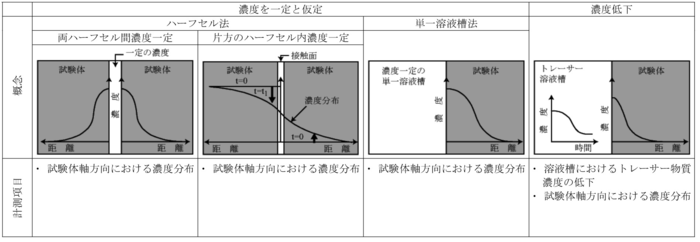
一般に，浸入拡散法により得られる試験結果は「みかけ」の拡散係数である．浸入拡散法はその試験原理により表1-15に示すようにさらに定量トレーサー法，濃度低下法の２つの方法に分類される．

 

  • 表1-15　浸入型室内拡散試験の試験方法

 

  • 定量トレーサー法：

定量トレーサー法はさらにハーフセル法，インハーフセル法，単溶液槽法の３つに分類される．

 

  • ハーフセル法：

ハーフセル法では，試験体を二つのセル内に充填もしくは装着し，両試験体の間に定量のトレーサー溶液を挟み，トレーサーを拡散させる（Cho et al.，1993；Kozaki et al., 1999；Idemitsu et al.，1990）．ある程度時間が経過した後に両試験体内のトレーサー分布を計測し，試験体を無限長と仮定する近似解により試験評価を行う．インハーフセル法では，試験前に試験体を二つのセル内に充填もしくは装着し，片方の試験体に一定量のトレーサーを浸透させる（Gillham et al.，1984）．試験は二つの試験体を密着させることで始まり，得られる計測データは一定時間後における試験体内の濃度分布（スライスする必要がある）であり，試験体を半無限長と仮定する解析解を用い試験評価が行われる．
単溶液槽法は試験体の一端に定濃度溶液槽を設け，他端をゼロフラックスとし，一定時間が経過した後の試験体内の濃度分布を計測する方法である．この方法では，試験を開始し終了するまでに濃度計測を行わないため試験管理は容易である．トレーサーとして放射性物質を用い，ガイガーカウンターを使用すると試験体内の濃度分布を，試験体をスライスすることなく計測することが可能である．また，その簡易な試験手順から，ベントナイトやベントナイト混合土，粘土等，試験体を容易にスライスできる地盤材料に主に適用されている．

 

  • 濃度低下法：

この試験法は前述の単溶液槽法と同様の手順で行われるが，溶液槽内の濃度の経時的な変化も計測することにより実効拡散係数と遅延係数の評価も可能となる．この場合の試験評価は数値解を用いて行われる（Rowe and Booker，1988）が，Takeda et al.（2006）は数値解による試験評価の誤差を低減するために，解析解を導出している．この試験法の利点は実効拡散係数および「みかけ」の拡散係数が一回の実験により評価される点にある．しかしながら，この試験法の実施例は少ない（Van et al., 2005）．
③浸出拡散法（Out-diffusion method）

浸出拡散法は試験前に試験体内にトレーサーを浸入させ，その後，試験体両端に溶液槽を設置しトレーサーを溶液槽側に浸出させる方法である．浸出拡散法は試験体内の初期濃度の分布により表1-16に示すように２つに分類される．

初期線形濃度分布法：この方法は透過拡散法の 定濃度浸入−定濃度浸出法の後に，試験体内に線形分布した濃度を両端の溶液槽内の溶液を濃度０の溶液に置換し，両端の溶液槽に浸出するトレーサー濃度を経時的に計測する方法である．この方法は，定濃度浸入−定濃度浸出法とのクロスチェックのために実施される（Jakob et al.，1999；Tits et al.，2003）．

 

  • 初期一様濃度分布法：

この方法では試験前に試験体内に一様にトレーサーを分布させ，前述の方法と同様に試験体両端に溶液槽を設け，浸出するトレーサー濃度の変化を計測する（Lever，1986）．この方法では試験前に一様にトレーサーを試験体に分布させる必要があるため，準備に長時間を要するとともに，一様に分布したかの確認ができない．

 

  • 表1-16　浸出型室内拡散試験の試験方法

 

透水及び拡散試験支配方程式の相似性

透水試験の支配方程式はダルシー則と飽和状態における水流の一次元連続式より導くことができ，式(8)に示す通りとなる（土質工学会，1980；張・竹田，2004）．

\frac{\partial H}{\partial t} = \frac{K}{S_s} \cdot \frac{\partial^2 H}{\partial x^2} (8)

ここに，Hは水頭；xは距離；Ssは比貯留率；Kは透水係数；tは時間である．拡散試験の支配方程式はフィックの第2法則（Fick’s Second Law）に基づくもので，次式（9）で表わされる（Neretnieks, 1980；Zhang and Takeda, 2005）．

\frac{\partial c}{\partial t} = \frac {D_e}{\alpha} \cdot \frac{\partial^2 c}{\partial x^2} (9)

ここで，cは濃度；xは同様に距離；Deは実効拡散係数；αは岩石保持因子（Rock capacity factor）と呼ばれるパラメータで，次式（10）に示す通り岩石の空隙率(εtot)，吸着係数(Kd)及び岩石密度(ρ)より決定される．

\alpha = \epsilon_{tot} + K_d \cdot \rho （10）

式（8）と式（9）を比較すると，透水と拡散は物理現象として異なるものの，数式的には類似の数理モデルで記述できることが分かる．すなわち，透水試験の水頭，透水係数及び比貯留率を拡散試験の濃度，実効拡散係数及び岩石保持因子に置き換えれば，透水試験の理論解を変換し，拡散試験の結果解析に利用することが可能である．逆に，拡散試験の濃度，実効拡散係数及び岩石保持因子を透水試験の水頭，透水係数及び比貯留率に置き換えれば，拡散試験の解析解を変換し，透水試験の結果解析に利用することも可能である．このため，ある境界条件下での透水試験に対する理論的評価の結論と知見を用い，対応する類似の境界条件下での拡散試験解釈に活用することも可能である．例えば，後述する流入圧が一定・流出圧も一定に制御する室内定水位透水試験は，トレーサー溶液槽内濃度が一定・計測溶液槽内濃度も一定に制御する従来型の室内拡散試験と対応させることが可能である．

 

室内透水試験

透水係数を直接的に計測する室内透水試験法として定水位法と変水位法のあることがよく知られており，また地盤工学分野で広く利用されてきている（土質工学会，1980）．一般的に，定水位法は比較的高い透水係数の試験体（10-2〜10-3cm/s），変水位透水試験は比較的低い透水係数の試験体（10-3〜10-6cm/s）に用いられる．試験方法が簡単であるため，実際に定水位法で10-3 cm/s，変水位法で10-9 cm/sまで計測したケースも多い．しかし，変水位法で10-6 cm/ｓよりも小さい透水係数を計測する場合，水頭の低下が小さいため，定水位法の式，すなわち周知のダルシー式で透水係数を求めることが殆どである．

難透水性試験体の透水試験をより速く計測するために，フローポンプ法とも呼ばれる定微流量法（Olsen, 1966）及びパルス法（Brace et al., 1968）も60年代に提案されていたが，試験装置と試験手順の煩雑さなどから近年まではあまり普及・利用されていなかった．

上記試験法のほか，遠心力透水試験法（Nimmo and Mello, 1991）及び間隙水圧振動法（Kranz et al., 1990）なども提案されているが，まだ一般的な手法として広く用いられていない．また，遠心力透水試験法も間隙水圧振動法も自然岩盤における低い動水勾配を再現することが難しく，間隙水圧振動法はさらにパルス法などより長い試験時間を要する．地下深部岩盤における地下水流動条件の再現性や試験の効率などの観点から，ここでは遠心力透水試験法と間隙水圧振動法に関する考察は控える．

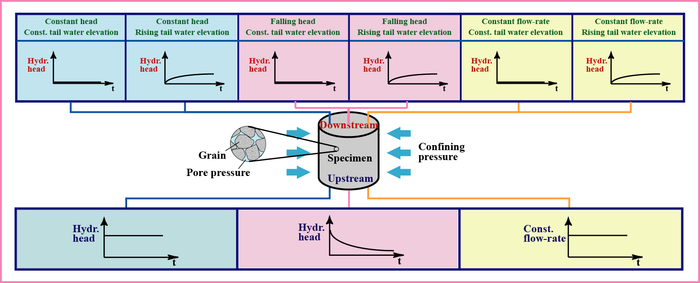
室内透水試験の精度，適用条件及び各種試験法の相対的優位性などを体系的に検討・評価するために，産総研では新しい厳密解析解の確立や，試験中における試験体内の動水勾配の経時的変化の定量的評価（Esaki et al., 1996; Zhang et al., 1997; Zhang et al., 1998; Zhang et al., 2000a; Zhang et al., 2000b; Zhang et al., 2002），境界条件を基準にした新しい分類の提案（Zhang et al.，2006b），代表的試験体を用いた検証・比較試験（Zhang et al., 2002；2004）及び無次元化した感度解析と総合的比較などを行ってきた（Takeda et al., 2007）．以下，境界条件を基準にした透水試験の分類と拡散試験に類似境界条件のない定微流量透水試験の解析理論と感度解析を示す．

境界条件を基準にし，従来の定水位及び変水位法を含む室内透水試験法は（図1-15）に示す3タイプ，6種類に分類することが可能である．すなわち，定流入水位法，変動流入水位法（パルス法）及び定微流量法の3タイプで，それぞれのタイプにおいては流出側の水位もしくは水頭が一定あるいは上昇（Rising tail water elevation）の2種類もあり，計6種類の透水試験が理論および実験的に実施することが可能である（Zhang, 2008）．従来の定水位透水試験および変水位透水試験はそれぞれ定流入水位・定流出水位，及び変動流入水位・定流出水位透水試験に対応し，従来の変水位法はパルス法の特例として定義することができる．

  • 図1-15 境界条件に基づく室内透水試験の分類．

拡散試験に類似境界条件のない定微流量透水試験の解析モデルを表1-17に示す．流入側の境界条件として，一定の微流量Qで試験体へ水を注入し，流出側の境界条件として，水頭上昇（rising tail water elevation）或いは定水位（constant tail water elevation）とする．

 

  • 表1-17　定微流量透水試験の解析モデル．

表1-17に示す支配方程式，初期および境界条件を用い，それぞれの境界条件に対応した解析解が導かれる．
定微流量－定水位（以降CF-CHと記する）の理論解は次の式（11）と（12）より表すことができる（Esaki et al., 1996; Zhang et al., 1997; Takeda et al., 2007）．

h(\xi,\tau) = \xi-2 \times \sum_{m=1}^{\infty} \frac{\exp (-\phi^2_m \cdot \tau) \cdot \sin (\phi_m \cdot \xi)} {\phi_m^2 \cdot (1+\beta_u + \beta_u^2 \cdot \phi_m^2) \cdot \sin (\phi_m)} （11）

\tan (\phi_m) = \frac{1}{\phi_m \cdot \beta_u} （12）

また，定微流量－水頭上昇（以降CF-VHと記する）の理論解は次式(13)と（14）より表すことができる（Song et al., 2004; Takeda et al., 2007）．

h(\xi,\tau) = \cfrac{\tau}{\beta_d + \beta_u +1} + \cfrac{(2 \cdot \beta_d + \xi) \cdot \xi}{2 \cdot (\beta_d + \beta_u +1)} -\cfrac{\beta_d + \beta_u + 2 \cdot \beta_d \cdot \beta_u + \cfrac{1}{3}} {2 \cdot (\beta_d + \beta_u +1)^2} - 2 \times

\sum_{m=1}^{\infty} \cfrac{ \exp (- \phi_m^2 \cdot \tau) \cdot (\phi_m^2 \cdot \beta_d \cdot \beta_u -1) \cdot \{\beta_d \cdot \phi_m \cdot \sin(\phi_m \cdot \xi) - \cos(\phi_m \cdot \xi)\}}{ \phi_m^2 \cdot [\beta_d^2 \cdot \beta_u^2 \cdot \phi_m^4 + \{\beta_d^2 \cdot (\beta_u +1) + \beta_u^2 \cdot (\beta_d +1)\} \cdot \phi_m^2 + (\beta_d + \beta_u +1)] \cdot \cos(\phi_m)} (13)

\tan(\phi_m) = \frac{\phi_m \cdot (\beta_d + \beta_u)}{\phi_m^2 \cdot \beta_d \cdot \beta_u -1} (14)

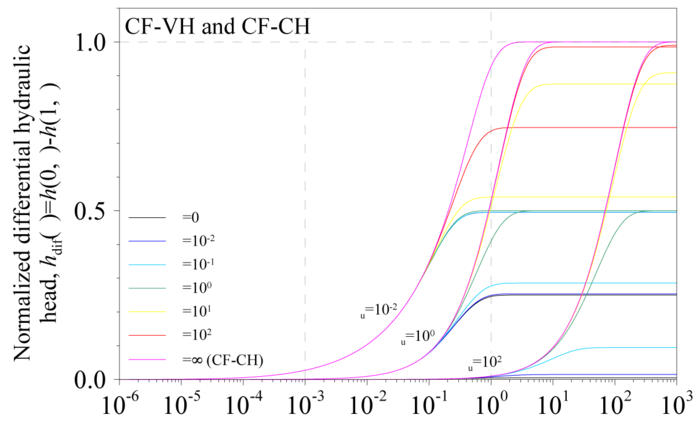
上記の解析解を利用すれば，最適試験条件の設定や境界条件を忠実に考慮したデータの解析などを実施することが可能である．図1-16に無次元変数および変数間の相対関係が透水試験に及ぼす影響を示す．図中横軸は無次元化した時間であり，縦軸は無次元化した試験体両端面間の差圧である．また，γは流出側貯留槽の圧縮貯留率と流入側貯留槽（通常は定微流量ポンプのシリンダーと配管から構成される）の圧縮貯留率との比である．図1-16によれば，試験体の貯留性に対して，流入側貯留槽の圧縮貯留性(βuの値)が小さければ小さいほど，透水試験に必要な時間を短縮できることが分かる．また，流出側の貯留槽を適切に小さくすることによって，実験終了に必要な時間も短縮できることが分かる．上記の解析解を用い，各々の変数に対する微分をすれば，計測データとなる試験体両端面間における差圧力に対する感度の解析も可能であるが，解析のプロセスは後述する拡散試験と類似するため，ここでは割愛する．

  • 図1-16　各変数が定微流量透水試験に及ぼす影響．

室内透水試験に関する知見を以下に要約する．

  • 定微流量法は他の2タイプの透水試験に比べ，試験中における試験体内の動水勾配の変化が小さく，また，最大動水勾配の発生も定微流量を適切に小さく設定することによって制御できるため，自然地層における低動水勾配を再現する技術面において優位性を持つ．
  • 難透水性岩石の透水係数をより短時間で計測するためには，試験体の高さを適切に小さくし，断面積を適切に大きくすることが有効である．試験体の高さを適切に短縮する際には，岩石鉱物粒子や内部微小クラックの大きさを考慮し，岩盤マトリクスの代表性を反映できる必要最小限の高さに設定する必要がある．
  • 厳密解析理論に基づく非定常解析は，透水試験の初期データを含むすべての計測データを有効に利用することができ，透水試験に必要な時間を短縮することができるだけでなく，データのクロスチェックや試験体の透水係数と比貯留係数の両者を同時に算出することも可能となる．
  • 変動流入水位法・上昇流出水位法，すなわちパルス透水試験は他の透水試験より計測に必要な時間が短いが，比貯留率の計測精度は透水係数や，装置の圧縮貯留率および水の圧縮率を含む透水システムの圧縮貯留性に依存されるため，感度解析，利用する計測機器の感度および動的応答特性を考慮した設計が必要不可欠である．
  • 透水試験の非定常状態の測定結果を利用して試験体の透水係数を算出する際には，厳密解析理論を適用するか，透水試験システムの圧縮貯留率を実験的に求める必要がある．従来のパルス透水試験では，装置および水の圧縮性を含む透水システムの圧縮貯留率は純水の圧縮率を利用するケースが殆どであり，透水係数は数倍〜数百倍までも小さく評価される可能性がある．このため，既存の文献に報告されている透水係数を参照・利用する際には，十分な注意を払う必要がある．
  • 岩石の透水特性は応力レベルのみならず，応力の載荷履歴にも影響を受ける．地下深部から採取した岩石コアの透水特性を評価する際には，応力の解放および再載荷による影響も考慮する必要がある．

 

室内拡散試験

拡散現象は移流と同様に地層における核種・物質移行に影響を与え，特にバリア機能を期待する難透水性地層においては物質移行の一つの支配的な要因である．文献調査からは，多くの試験結果と報告論文が得られるが，特定の研究機関もしくは研究者は特定の試験法を用い，体系性のある研究は皆無に近い．また，殆どの研究・報告では，境界条件を簡略に仮定した簡易解析を利用してデータの解析を行われており，解析の精度については十分な検討が行われていないのが現状である． Zhang and Takeda（2005）が透過型室内拡散試験に対して行った理論的評価によれば，測定溶液槽における濃度の上昇を無視した従来の簡易解析では，試験体の実行拡散係数および岩石保持因子の両者とも過少評価されることが判明している．従って，室内拡散試験の条件を適切に設計し，試験データを適切に解析するためには，境界条件を忠実に記述する解析理論の整備が必要である．ここでは，境界条件を基準に，室内拡散試験法の再分類を行い，各試験法に対応した解析理論の整理と必要な新理論解の確立，無次元の統一尺度に基づく感度解析および総合的検討・比較を行った結果を示す（Zhang et al., 2006a; Takeda et al., 2006; Takeda et al., 2008a；b）．

境界条件に基づき室内拡散試験は透過型拡散試験（Through Diffusion Test），浸入型拡散試験（In Diffusion Test），滲出型拡散試験（Out Diffusion Test）およびカラム試験（Column Test）に大別することができる（Zhang et al., 2006a）．

透過型室内拡散試験はトレーサー溶液槽および計測溶液槽における濃度の変化パターンの組み合わせによってさらに4種類に細分類することができる（表1-18）．従来の透過型拡散試験はトレーサー濃度が一定，測定溶液槽内の濃度も一定と仮定したもとで解析を行ってきているケースが多いが，実際の試験条件はトレーサー濃度が一定，測定溶液槽内の濃度が上昇する．解析の仮定と実際の試験条件との乖離によって，試験結果の解釈に誤差が生じることになる（Zhang and Takeda, 2005）．トレーサー溶液槽内の濃度低下および測定溶液槽内の濃度上昇を考慮した透過型試験法は試験管理上利便性があることが実証されている（Zhang et al., 2006b）．
浸入型室内拡散試験も同様に，境界条件の差違によってさらに4種類に細分類することが可能である（表1-19）．一般的に，浸入型室内拡散試験は，トレーサーの濃度が一定と仮定し，試験後における試験体内の濃度分布を分析・測定し，試験体の長さが無限と仮定した簡易解を利用して解析するものがほとんどである．Nakajima et al. （2007）の理論研究によれば，浸入型室内拡散試験では，試験体の長さを実際の通りで有限とし，また，滲出側の境界条件をフラックスなしと記述する解析解が有効である．

滲出型拡散試験およびカラム試験に関してはZhang et al. （2006a）が詳しい．以下，透過型室内拡散試験の理論的整備と評価結果を示す．

 

  • 表1-18　透過型室内拡散試験の細分類．

 

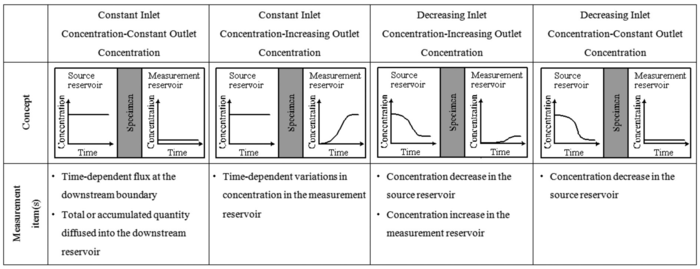
  • 表1-19　浸入型室内拡散試験の細分類．

 

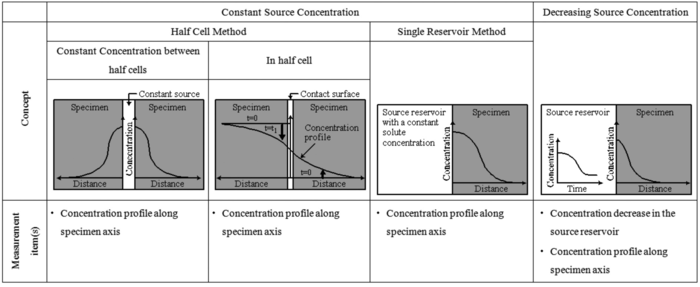
  • 表1-20　透過型室内拡散試験の解析モデル．

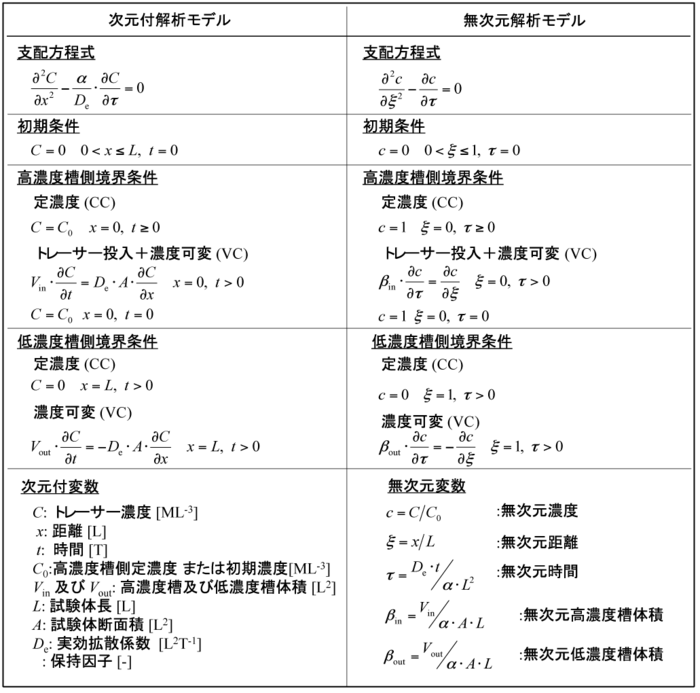
表1-20に透過型室内拡散試験の次元付および無次元化した解析モデルを示す．表1-18に示す各概念図に対して，ここでは，濃度の上昇（Increasing）或いは低下（Decreasing）を変化（V:Varying）で記している．また，高濃度槽および低濃度槽はそれぞれ上流のトレーサー溶液槽と下流の測定溶液槽を意味する．

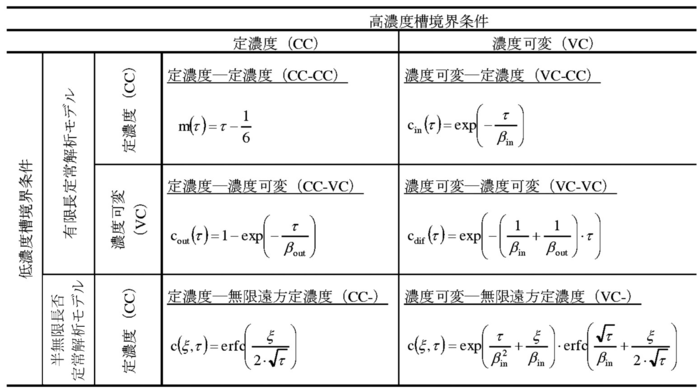
表1-20に示す支配方程式，初期および境界条件より，各種境界条件に対応した透過型室内拡散試験の理論解を導くことが可能であり，表1-21に示す．比較を行うために，従来の簡易解を表1-22に示す．

 

  • 表1-21　透過型室内拡散試験の厳密解．

 

  • 表1-22　透過型室内拡散試験の簡易解．

  • 図1-17　透過型室内拡散試験の簡易解析の適用範囲．

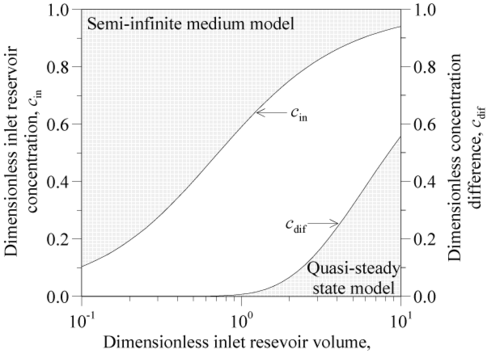
室内透水試験と同様に，厳密な解析解を利用すれば，各変数の試験に対する影響を定量的に評価することが可能である．ここでは，解析解の適用例として，従来の簡易解の適用範囲もしくは条件に関する検討結果（図1-17）を紹介する．

図1-17では，横軸は岩石試験体の吸着容量を基準に無次元化した高濃度槽の容積，左の縦軸はトレーサーの初期濃度を基準に無次元化したトレーサー溶液槽（高濃度槽）内の濃度，右の縦軸はトレーサーの初期濃度を基準に無次元化した高濃度槽および低濃度槽内の濃度差である．この図によれば，試験体の長さを半無限と仮定した簡易解は，試験の初期段階の計測データにしか適用できないことが分かる．例えば，無次元のトレーサー溶液槽の容積が10である場合，トレーサー溶液槽内の濃度低下が約5%以上達した場合，簡易解はもう適用できなくなることが分かる（図の右上の部分で示す試験条件に対応）．逆に準定常モデルは試験の後半の計測データの解析にしか適用できない．拡散試験は比較的長い計測期間を要するため，試験後半の計測データを用いる準定常解析は極めて非効率的である．なお，それぞれの境界条件に対応した解析解を適用すれば，試験の初期から計測の最後までのすべてのデータを直接利用することができ，試験効率と解析精度を向上することが可能である．

室内拡散試験に関して行ってきた一連の理論的検討より，以下に示す知見が得られた．

  • 室内拡散試験は古くから利用されてきており，数多くの実施・実測例があるが，境界条件を簡略に仮定した簡易解による解析結果には評価誤差が生じている．
  • 簡易解に基づくデータ解析は，岩石の吸着特性を含む岩石保持因子の評価で大きな誤差を生じる．吸着は遅延効果の重要ファクターであるため，解析解を用いて，岩石保持因子を正確に評価する必要がある．
  • ここで整備された各種室内拡散試験の解析理論は対応する各種室内拡散試験条件の設定，試験結果の適切評価および試験手法間の総合的比較・検討に有効である．
  • 岩石の実効拡散係数は透水係数と同様に，応力および載荷履歴の関数であると考えられるが，既存研究では，応力の状態を再現した拡散試験は皆無に近い．応力の影響を考慮した実効拡散係数のデータ蓄積および関連知見の整備は継続的に行う必要がある．

引用文献

Allison,G.B. and Hughes,M.W. (1983) The use ofnatural tracers as indicators of soil-watermovement in a temperate semi-arid region. Jour.Hydrol, 60, 157-173.

ASTM (2002) Standard test method for determining transmissivity and storativity of low-permeability rocks by in situ measurements using pressure pulse technique. Annual Books ofASTM Standards, 4(8), 778-783.

ASTM (2006) Standard guide for comparison of techniques to quantify the soil-water (moisture) flux. ASTM, D6642-01.

Barnes,C.J. and Allison,G.B. (1984) The distribution of deuterium and 18O in dry soils: 3. Theory for non-isothermal water movement. Jour.Hydrol., 74, 119-136.

Brace,W.F., Walsh,J.B. and Frangos,W.F. (1968) Permeability of granite under high pressure. Jour. Geophys. Res., 73, 2225-2236.

Bredehoeft, J.D. and Papadopulos, S.S. (1980) A method for determining the hydraulic properties for tight formations. Water Resources Research, 16(1), 233-238.

Butler, J.J., Jr. (1997) The Design, Performance//Analysis of Slug Tests CRC Press LLC, Florida, 252.

Cho,W.J., Oscarson,D.W. and Hahn,P.S. (1993) The measurement of apparent diffusion coefficients in compacted clays: An assessment of methods. Appl. Clay Science, 8, 283-294.

Cooper,H.H., Bredehoeft,J.D. and Papadopulos,I.S. (1967) Response of a finite-diameter well to aninstantaneous charge of water. Water Resources Res., 3, 263-269.

土質工学会 (1980) 土質試験法 757p.

Dougherty, D.E. and Babu D.K. (1984) Flow to a Partially Penetrating Well in a Double-Porosity Reservoir. Water Resources Research, 20(8), 1116-1122.

Drew, D. J. and Vandergraaf, T. T. (1989) Construction and Operation of a High-Pressure Radionuclide Migration Apparatus. Atomic Energy of Canada Limited, TR-476, 23pp.

Esaki, T., Zhang, M., Takeshita, A. and Mitani, Y. (1996) Rigorous Theoretical Analysis of a Flow Pump Permeability Test. Geotechnical Testing Journal, 19(2), 181-190.

Fischer,G.J. (1992) The determination of permeability and storage capacity: pore pressure oscillation method, in Fault Mechanics and Transport Properties of Rocks, eds Evans, B, and Wong, T.-F. Academic Press, 187-211.

Garcia Gutierrez,M., Cormenzana,J.L., Missana,T. and Mingrarro,M. (2004) Diffusion coefficients and accessible property for HTO and 36Cl in Compacted FEBEX Bentonite. Appl. Clay Sci., 26, 65-73.

Gillham,R.W., Robin,M.L.J., Dytynyshyn,D.J. and Johnston,H.M. (1984) Diffusion of nonreactive and reactive solutes through fine-grained barrier materials. Canadian Geotech. Jour., 21, 541-550.

Hsieh, P. A., Tracy, J. V., Bredehoeft, J. D. and Silliman and S. E. (1981) A Transient Laboratory Method for Determining the Hydraulic Properties of ‘Tight’ Rocks-1. Theory Int. J. Rock Mech. Min. Sci. & Geomech, 18, 245-252.

Hvorslev,M.J. (1951) Time lag and soil permeability in ground-water observations. USACE Waterways experiment station, 36.
Hyder, Z., Butler, J.J., Jr., McElwee, C.D. and Liu, W. (1994) Slug Tests in Partially Penetrating Wells. Water Resources Research.

Idemitsu,K., Ishiguro,K., Yusa,Y., Sasaki,N. and Tsunoda,N. (1990) Plutonium diffusion in compacted bentonite. Engineer. Geol., 28, 455-462.

伊藤芳郎・斉藤輝夫・市川　浩・南雲政博・川口英雄・竹内篇雄 (1984) 地下水流速の新しい測定法の試み−流動電位法−．日本地下水学会誌26, 4, 77-96.

Jakob,A., Sarott,F.A. and Spieler,P. (1999) Diffusion and sorption on hardened cement pastes – Experiments and modelling results. Waste Manage. Lab. PSI-Bericht., May-95.

地盤工学会 (1980) 土質試験法．地盤工学会 .

地盤工学会 (1995) 地盤調査法．地盤工学会.

小松田精吉 (1990) 流速･流向の測り方 地質と調査, 3, 21-27.

Kozaki T., Sato Y., Nakajima M., Kato H., Sato S. and Ohashi H. (1999) Effect of particle size on thediffusion behavior of some radionuclides in compacted bentonite. Jour Nuclear Materials., 270, 265-272.

Kranz,R.L., Saltzman, J.S. and Blacic,J.D. (1990) Hydraulic diffusivity measurements on laboratory rock samples using an oscillating pore pressure method. Jour. Rock Mech., MiningSci. & Geomech. Abst., 27, 345-352.

Lever,D.A. (1986) Some notes on experiments measuring diffusion of sorbed nuclides through porous media. Harwell Report, AERE R12321.

Martinez-Landa, L. and Carrera, J. (2005) An Analysis of Hydraulic Conductivity Scale Effects in Granite (Full-scale Engineered Barrier Experiment (FEBEX), Grimsel, Switzerland). Water Resources Research, 41(3), doi:10.1029/2004WR003458.

Moench, A.F. (1985) Transient Flow to a Large-Diameter Well in an Aquifer With Storative Semiconfining Layers. Water Resources Research, 21(8), 1121-1131.

Nakajima, H., Takeda, M., Zhang, M. and Hiratsuka, T. (2006) Quantitative Evaluation of Possible Errors Induced by Using Simplified Analytical Solutions to the Laboratory In-Diffusion Test.

Neretnieks, I. (1980) Diffusion in the Rock Matrix: An Important Factor in Radionuclide Retardation? Journal of Geophysical Research, 85(B8), 4379-4397.

Neuzil,C.E., Cooley,C., Silliman,S.E., Bredehoeft,J.D. and Hsieh,P.A. (1981) A transient laboratory method for determining the hydraulic properties of tight rocks − II. Application. Inter. Jour. Rock Mech., Mining Sci. & Geomech.Abst., 18, 253-258.

Nimmo, J. R. and Mello, K. A. (1991) Centrifugal Techniques for Measuring Saturated Hydraulic Conductivity. Water Resources Research, 27, 1263-1269.

西垣　誠 (1991) 地下水の流向･流速．土と基礎39, 8, 56-58.

Novakowski, K.S. (1993) Interpretation of the Transient Flow Rate Obtained From Constant-Head Tests Conducted in Situ in Clays. Canadian Geotechnical Journal, 30, 600-606.

OECD/NEA (2000) Features, Events and Processes (FEPs) for Geological Disposal of Radioactive Waste: An International Database.

Olsen, H. W. (1965) Deviation from Darcy’s Law in saturated clays. Soil Sci. Soc. Amer. Proc., 29, 135-140.

Olsen, H. W. (1966) Darcy’s Law in Saturated Kaolinite. Water Resources Research, 2(6), 145-157.

Olsen,H.W., Morin,R.H. and Nichols,R.W. (1985) Flow pump applications in triaxial testing, advancedtriaxial testing of soil and rock. ASTM-STP, 977, 68-81.

Papadopulos, S. S., J. D. Bredeoet, and Cooper,H.H.l. (1973) On the analysis of ‘slug test’ data. Water Resources Res. 9, 1087-1089.

Phillips,F.M., Mattick,J.L. and Duval,T.A. (1988) Chlorine-36 and tritium from nuclear-weapons fallout as tracers for long-term liquid and vapormovement in desert soils. Water Resources Res., 24, 1877-1891.

Pickens, J.F., Grisak, G.E., Avis, J.D., Belanger, D.W. and Thury, M. (1987) Analysis and Interpretation of Borehole Hydraulic Tests in Deep Boreholes: Principles. Model Development//Applications Water Resources Research, 23(7), 1341-1375.

Rebour,V., Billiotte,J., Deveughele,M., Jambon,A. and Guen,C.L. (1997) Molecular diffusion in water-saturated rocks: A new experimental method. Jour. Contaminant Hydrol., 28, 71-93.

Rowe,R.K. and Booker,J.R. (1984) The analysis of pollutant migration in a non-homogeneous soil. Geotechnique, 34, 601-612.

佐倉保夫 (1984) 温度による地下水調査法．日本地下水学会誌, 26, 4.

Sato,H., Shibutani,T. and Yui,M. (1997) Experimental and modeling studies on diffusion of Cs, Ni and Sm in granodiorite, basalt and mudstone. Jour. Contaminant Hydrol., 26, 119-133.

Sharma,M.L. and Hughes,M.W. (1985) Groundwater recharge estimation using chloride, deuteriumand oxygen-18 profiles in the deep coastal sandsof western Australia. Jour. Hydrol., 81, 93-109.

鹿園直建 (1995) 地下水・熱水移行シナリオとナチュラルアナログ研究　放射性廃棄物と地質科学：地層処分の現状と課題．東京大学出版社, 389p.

Skagius, K. and Neretnieks, I. (1986) Diffusivity Measurements and Electrical Resistivity Measurements in Rock Samples Under Mechanical Stress. Water Resources Research, 22(4), 570-580.

Song,I., Elphick,S.C., Main,I.G., Ngwenya,B.T., Odling,N.W. and Smyth,N.F. (2004) One-dimensionalfluid diffusion induced by constant-rate flowinjection: Theoretical analysis and application to the determination of fluid permeability and specific storage of a cored rock sample. Jour. Geophy. Res., 109, B05207.

高橋　学・張　銘・江崎哲郎・坂井健太郎 (1998) 室内透水試験法について．応用地質, 39, 315-321.

高橋美紀・金子貴信・里　優 (2003) 間隙圧オシレーション法による浸透率測定と測定プログラム．石油開発技術センター研究報告 大型研究「トラップの形成・シール能力評価技術」特集号, 121-132.

Takeda, M., Zhang, M. and Nakajima, H. (2006) Strategies for Solving Potential Problems Associated with Laboratory Diffusion and Batch Experiments-Part 2: Future Improvements. Proceedings of Waste Management Symposium 2006, (CD-ROM).

Takeda, M., Zhang, M., Hiratsuka, T. (2007) Cross-evaluation of laboratory permeability tests by dimensionless analysis AGU Fall Meeting, San Francisco, USA.

Takeda, M., Nakajima, H., Zhang, M. and Hiratsuka, T. (2008a) Laboratory Longitudinal Diffusion Tests: 1. Dimensionless Formulations and Validity of Simplified Solutions. Journal of Contaminant Hydrology, 97, 100-116.

Takeda, M., Zhang, M., Nakajima, H. and Hiratsuka, T. (2008b) Laboratory Longitudinal Diffusion Tests: 2. Parameter Estimation by Inverse Analysis. Journal of Contaminant Hydrology, 97, 117-134.

Tits,J., Jakob,A., Wieland,E. and Spieler,P. (2003) Diffusion of tritiated water and 22Na+ through non-degraded hardened cement pastes. Jour. Contaminant Hydrol., 61, 45-62.

内田洋平・佐倉保夫・荒川隆付 (1993) 温度をトレーサーとした山形盆地における地下水流動の研究．日本地下水学会1993年春季講演会講演要旨, 90-95.

Van Loon,L.R., Baeyens,B. and Bradbury,M.H. (2005) Diffusion and retention of sodium and strontium in Opalinus Clay: Comparison of sorption data from diffusion and batch sorption measurements,and geochemical calculations. Appl. Geochem., 20, 2351-2363.

Zhang, M., Esaki, T., Olsen, H. and Mitani, Y. (1997) Integrated Shear and Flow Parameter Measurement. Geotechnical Testing Journal, 20(3), 296-303.

Zhang,M., Takahashi M., Morin,R.H. and Esaki T. (1998) Theoretical evaluation of the transient response of constant head and constant flow rate permeability tests. Geotech. Test. Jour., 21, 52-57.

Zhang,M., Takahashi M., Morin,R.H. and Esaki T. (2000a ) Evaluation and application of the transient-pulse technique for determining the hydraulic properties of low-permeability rocks-part 1: Theoretical evaluation. Geotech. Test.Jour., 23, 83-90.

Zhang,M., Takahashi M., Morin,R.H. and Esaki T. (2000b ) Evaluation and application of the transient-pulse technique for determining the hydraulic properties of low-permeability rocks-part 2: Experimental application. Geotech. Test.Jour., 23, 91-99.

Zhang,M., Takahashi M., Morin,R.H., Endo H. and Esaki T. (2002) Determining the hydraulic properties of saturated, low-permeability geological materials in the laboratory: Advances in theory and practice, evaluation and remediation of low permeability and dual porosity environments. ASTM STP, 1415, 83-98.

Zhang, M. and Takeda, M. (2003) Physical, Mechanical and Hydraulic Properties of Inada Granite and Shirahama Sandstone in Japan. Proceedings of International Symposium on the Fusion Technology of Geosystem Engineering, Rock Engineering and Geophysical Exploration, 206-213.

Zhang, M., Takeda, M. and Aung, T. T. (2004) Simultaneous Determination of the Hydraulic Conductivity and Specific Storage of a Test Specimen from Laboratory Permeability Tests. American Geophysical Union Fall Meeting, San Francisco, USA.

Zhang, M. and Takeda, M. (2005) Theoretical Evaluation of the Through-Diffusion Test for Determining the Transport Properties of Geological Materials. Proceedings of Waste Management Symposium 2005, (CD-ROM).

Zhang, M., Takeda, M. and Nakajima, H. (2006a) Strategies for Solving Potential Problems Associated with Laboratory Diffusion and Batch Experiments-Part 1: An Overview of Conventional Test Methods. Proceedings of Waste Management Symposium 2006, (CD-ROM).

Zhang, M., Takeda, M., Nakajima, H. (2006b) Fundamental Theories and Concepts for Developing a Versatile Laboratory Permeability Test System American Geophysical Union Fall Meeting, San Francisco, USA.

Zhang, M. (2008) Effects of Stress on Permeation and Diffusive Properties of Rocks. American Geophysical Union Fall Meeting, San Francisco, USA.

Zhang, M. (2009) Experimental Studies on Retardation Properties of Granite Specimens from Grimsel Test Site, Switzerland – 9368. Proceedings of Waste Management Symposium 2009, (CD-ROM).

張　銘・高橋　学・江崎哲郎 (1997) 室内透水試験における動水勾配の定量的評価について．資源・素材’97 秋季大会 論文集, 69-72.

張　銘・高橋　学・遠藤秀典 (2000) 原位置浸透流測定法について（その１）．応用地質, 41, 293-303.

張　銘・遠藤秀典・高橋　学 (2001) 原位置浸透流測定法について（その２）．応用地質, 42, 52-59.

張　銘・竹田幹郎 (2004) 地質媒体における物質移行特性の評価手法について 地質ニュース, 602, 25-35.