大気中における化学物質の動態(4)
大気中化学物質の沈着(その1)
第4回:大気中における化学物質の動態(4)
大気中化学物質の沈着(その1)
1.はじめに
大気中に存在する化学物質が地表面に移行する過程を沈着といいます。沈着は,湿性沈着と乾性沈着に分けられます。
湿性沈着は大気中のガス状の物質と浮遊粒子に吸着した物質を降雨水が吸収,捕捉することにより,地表面に移行する過程をいいます。
乾性沈着は,ガス状物質が表層水や土壌に直接吸収されたり,浮遊粒子が地表面に降下したりすることにより移行する過程をいいます。
今回は,降雨水によるガス状物質の吸収について考えます。
2.薄膜理論によるガスの吸収
大気中に存在する水滴とその周囲の空気の境界層における化学物質の移動を分子拡散と考えると,物質の移動量(N,mole/m2/秒)はFickの式で表されます。

ここで,Cは濃度(mole/m3),Dは拡散係数(m2/秒),Zは移動方向の距離(m)です。
境界層で,濃度勾配(∂C/∂Z)が一定であれば,式(4-1)は以下の式で表わすことができます。

ここで,KはD/δで定義される質量移動係数(m/秒)です。
今,図4-1に示す空気(気相)と水滴(液相)の界面を考えます。

図4-1 空気と雨滴の界面
図4-1の界面の液相境界層での物質の移動量(Nsw,mole/m2/秒)は次式で表されます。

ここで,Klは液相中の化学物質の質量移動係数(m/秒)です。また,Cwは液相中の化学物質濃度(mole/m3)で,Cswは液相境界層の気液界面での化学物質濃度(mole/m3)です。
同様に,分子の気相での平均自由行程にほぼ一致するKnudsen領域での物質の移動量(Nk,mole/m2/秒)と気相境界層での物質の移動量(Nsa,mole/m2/秒)は,それぞれ以下の式で表されます。

ここで,kgは気相中の化学物質の質量移動係数(m/秒)です。αは調整係数(範囲:0.1~1)で,βは です(R:気体定数,T:温度[K],MW:化学物質の分子量)。また,Caは気相中の化学物質濃度(mole/m3),CkはKnudsen領域と気相境界層の界面での化学物質濃度(mole/m3),Csaは気相境界層の気液界面での化学物質濃度(mole/m3)です。
です(R:気体定数,T:温度[K],MW:化学物質の分子量)。また,Caは気相中の化学物質濃度(mole/m3),CkはKnudsen領域と気相境界層の界面での化学物質濃度(mole/m3),Csaは気相境界層の気液界面での化学物質濃度(mole/m3)です。
CsaとCswの間にはヘンリー則が成立するため,これらの濃度には次式で示す関係があります。ここで,Kawは気/液分配係数です。

式(4-4)と式(4-5)から,CsaはCaと以下の式で関係付けられます。

したがって,式(4-6)と式(4-7)から,CswはCaと以下の式で関係付けられます。

各境界層での化学物質の移動速度は全体の移動速度に等しいため,これをNとすれば,上記の各式から次式が得られます。

この式(4-9)をNについて解くと,次式が得られます。
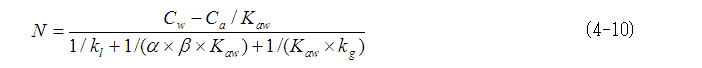
一般には,βは大きな値で, は0 とみなせますので,以下の式が得られます。
は0 とみなせますので,以下の式が得られます。

これが,Whitmanが考案した液相と気相間での物質の拡散移動に関するモデル(2薄膜理論)です。
平衡状態では,N = 0 となるため,空気中(気相)と雨水(液相)中の濃度比(Ca/Cw)は気/液分配係数であるKawに等しくなります。式(4-11)は,以下に示すように空気から雨滴への化学物質の吸収と雨滴から空気への化学物質の揮発に分離することができます。ここで,NdとNvはそれぞれ,吸収量と揮発量(単位はともにmole/m2/秒)です。
【吸収】

【揮発】

単位容積当りの揮発速度(Rv,mole/m3/秒)は気液界面の面積をA(m2),雨滴の容積をV(m3)とすると, ですので,揮発に対する1次速度定数(kv,1/秒)は次式で表わされます。
ですので,揮発に対する1次速度定数(kv,1/秒)は次式で表わされます。

ここで,rrainは雨滴を球形と仮定した場合の半径(m)です。
一般に,粒径が100μm程度の雨滴は1 cm3の空気中に1個の割合で存在し,その落下の終末速度は0.69 m/秒です。この場合,1 cm3中の空気の容積(Va)と雨滴の容積(Vrain)の比は1:5.2×10-7となります。前回の解説で示したようにガス態としての存在比率が高いダイオキシン異性体の2,3,7,8-TCDDでも,Kawは1.4×10-3であり,仮に雨滴とその周囲の空気中の2,3,7,8-TCDDの濃度に平衡状態が成立したとすると,雨滴中の2,3,7,8-TCDD濃度(Cw)と空気中濃度(Ca)を比べると,雨滴中濃度がかなり高いことになります。

一方,1 cm3中の空気中に占める雨滴容積の割合(Vrain/Va)は上記のように,5.2×10-7ですので,空気中と雨滴に存在する2,3,7,8-TCDD量(MaおよびMrain)の比は以下のように計算され,空気中の2,3,7,8-TCDDの雨滴への移行量はわずかであることがわかります。
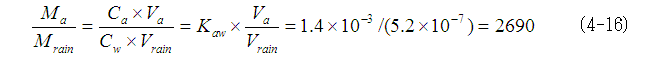
そこで,雨滴の周りの空気中(図4-1の気相)2,3,7,8-TCDD濃度は一定とみなすと,吸収され,揮発することに伴う雨滴中の2,3,7,8-TCDD濃度の時間変化(Cw(t))は次式で表わすことができます。

雨滴中濃度Cw(t)の平衡濃度Cw(∞)は式(4-17)のtを∞とすることにより, となります。したがって,空気中に存在するガス状の化学物質濃度と雨滴中濃度がほぼ平衡に到達する時間を雨滴中濃度が平衡濃度の95%に到達する時間(t’)は次式を満たすt’を算出すればよいことになります。
となります。したがって,空気中に存在するガス状の化学物質濃度と雨滴中濃度がほぼ平衡に到達する時間を雨滴中濃度が平衡濃度の95%に到達する時間(t’)は次式を満たすt’を算出すればよいことになります。

式(4-18)を解くことにより,以下の式を得ることができます。

今,雨滴の半径(rrain)を雲粒と雨滴の境目とされる50μmとし,気相と液相の質量移動係数のkgとklをそれぞれ3 m/時と0.03 m/時とします。式(4-14)から,2,3,7,8-TCDDの揮発速度定数kvは1.11×102 [1/時]となり,式(4-19)を用いて平衡濃度の95%に到達する時間(t’)は98秒と算出されます。半径50μmの雨滴の落下終末速度は0.69 m/秒ですから,98秒間に68 m程度,雨滴は落下することになり,落下中に空気中濃度と雨水中濃度はほぼ平衡に到達すると考えられます。
図4-2は,上記と同じ条件で,Kawを1×10-5~10まで変化させた場合の平衡濃度の95%に到達するのに必要な時間を示しています。

図4-2 Kawの変化に伴うt'の変化
図4-2から明らかなように,Kawが大きくなるにつれて,平衡とみなせる状態に到達する時間が短くなり,上記の条件(rrain:50μm,kg:3 m/時,kl:0.03 m/時)では,Kawが0.1以上になるとはほぼ一定の時間(12秒)となります。
以上のことから,大気中のガス状物質の雨水への濃縮倊率(Wv)を雨滴中濃度/空気中濃度(すなわち,Cw/Ca)とすれば,この倊率は気/液分配係数の逆数(Wv=1/Kaw)として求めることができます。
参考文献
Whiteman W.G. (1923): A preliminary experimental confirmation of the two-film theory of gas adsorption. Chem. Metall. Eng. 29: 146-148.
Goody R.M., Walker J.C.G.(安田敏明・根本順吉 訳)大気科学入門.共立出版.







 です(R:気体定数,T:温度[K],MW:化学物質の分子量)。また,Caは気相中の化学物質濃度(mole/m3),CkはKnudsen領域と気相境界層の界面での化学物質濃度(mole/m3),Csaは気相境界層の気液界面での化学物質濃度(mole/m3)です。
です(R:気体定数,T:温度[K],MW:化学物質の分子量)。また,Caは気相中の化学物質濃度(mole/m3),CkはKnudsen領域と気相境界層の界面での化学物質濃度(mole/m3),Csaは気相境界層の気液界面での化学物質濃度(mole/m3)です。




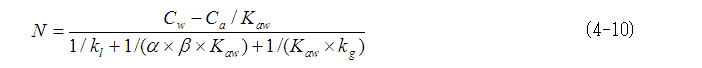
 は0 とみなせますので,以下の式が得られます。
は0 とみなせますので,以下の式が得られます。



 ですので,揮発に対する1次速度定数(kv,1/秒)は次式で表わされます。
ですので,揮発に対する1次速度定数(kv,1/秒)は次式で表わされます。


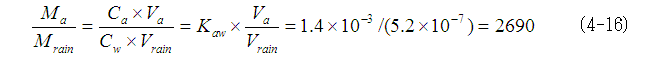

 となります。したがって,空気中に存在するガス状の化学物質濃度と雨滴中濃度がほぼ平衡に到達する時間を雨滴中濃度が平衡濃度の95%に到達する時間(t’)は次式を満たすt’を算出すればよいことになります。
となります。したがって,空気中に存在するガス状の化学物質濃度と雨滴中濃度がほぼ平衡に到達する時間を雨滴中濃度が平衡濃度の95%に到達する時間(t’)は次式を満たすt’を算出すればよいことになります。