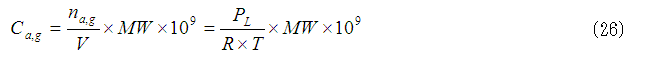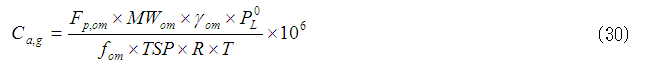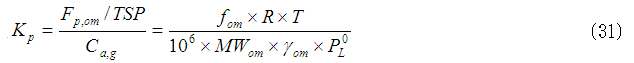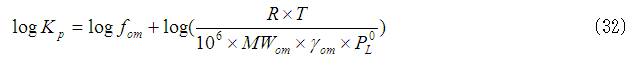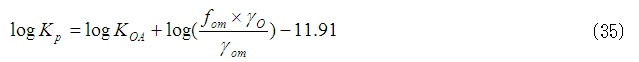第2回:大気中における動態(2)
第2回:大気中における化学物質の動態(2)
大気浮遊粒子への吸着,粒子/空気分配係数
1.はじめに
前回に引き続き今回も,化学物質の大気浮遊粒子への吸着について解説します。今回の内容は,浮遊粒子/ガス分配係数(particle/gas partition coefficient,Kp)についてです。
2.粒子/空気分配係数
前回,大気中の浮遊粒子に吸着される化学物質の割合(φ)を以下の式(1)で定義しました。

このφは大気中の浮遊粒子濃度(TSP,単位:μg/m3)を用いて,式(15)のように改変できます。

ここで;
Kp :浮遊粒子/ガス分配係数(単位:m3/μg)。浮遊粒子中の化学物質濃度(Cp,単位:ng/μg)と空気中の化学物質濃度(Ca,g,単位:ng/m3)の比(Cp/Ca,g)として定義される。
Caは浮遊粒子吸着態として存在する化学物質の大気中濃度(Ca,p,単位:ng/m3)と,Ca,p = Cp×TSPの関係があり,
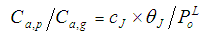 前回の解説,式(13)参照)ですので,KPはJunge定数(cJ)を用いて式(16)に示すように表されます。
前回の解説,式(13)参照)ですので,KPはJunge定数(cJ)を用いて式(16)に示すように表されます。

上式の両辺を対数変換すると,以下のように,Kpの対数値は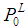 の対数値と傾き -1 の線形関係が得られます。
の対数値と傾き -1 の線形関係が得られます。

一般に,大気を実際に分析して得られるKpと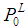 の間には以下の線形関係が成立すると報告されています。
の間には以下の線形関係が成立すると報告されています。

下表のように,都市域大気中多環芳香族炭化水素類の測定データから決定された傾き(mr )は,-1.09~ -0.631,切片(br )は,-5.95~ -4.61の範囲の値が報告されています。同様に,ポリ塩化ビフェニル(PCB)類に対しては,mr は,-0.946~ -0.715,br は,-5.86~ -5.14の値が報告されています。
表 既報の式(18)の傾き(mr )と切片(br )
| 空欄 |
測定場所 |
傾き |
切片 |
報告者 |
都市域
多環芳香族炭化水素類
多環芳香族炭化水素類
PCB類
多環芳香族炭化水素類
PCB類
PCB類
多環芳香族炭化水素類
多環芳香族炭化水素類
多環芳香族炭化水素類
多環芳香族炭化水素類
多環芳香族炭化水素類
塩素系農薬
ダイオキシン類
|
米国オレゴン州
米国コロラド州
米国コロラド州
米国イリノイ州
米国イリノイ州
米国イリノイ州
米国イリノイ州
米国バージニア州
英国ロンドン
日本大阪
コンゴ,ブラザビル
コンゴ,ブラザビル
米国インディアナ州
|
-0.882
-0.760
-0.946
-0.694
-0.726
-0.715
-0.745
-1.09
-0.631
-1.04
-0.810
-0.740
-0.775
|
-5.38
-5.10
-5.86
-4.61
-5.18
-5.14
-4.66
-5.75
-4.61
-5.95
-5.31
-5.76
-5.72
|
Ligockiら,1989
Foremanら,1990
Foremanら,1990
Cothamら,1995
Cothamら,1995
Harnerら,1999
Harnerら,1999
Gustafsonら,1997
Baekら,1991
Yamasakiら,1982
Ngabeら,1992
Ngabeら,1992
Bidlemanら,1997
|
田園地帯
多環芳香族炭化水素類
多環芳香族炭化水素類
多環芳香族炭化水素類
多環芳香族炭化水素類
多環芳香族炭化水素類
多環芳香族炭化水素類
塩素系農薬
PCB類,塩素系農薬
|
米国オレゴン州
スペリオル湖
スペリオル湖
米国グリーン湾
米国バージニア州
エリー湖,オンタリオ湖
エリー湖,オンタリオ湖
ドイツ,バイロイト
|
-0.724
-0.614
-0.586
-1.00
-0.649
-0.580
-0.688
-0.610
|
-4.94
-4.25
-3.83
-5.47
-4.43
-4.14
-5.06
-4.74
|
Ligockiら,1989
Bakerら,1990
McVeetyら,1988
Cothamら,1995
Harnerら,1999
Hoffら,1996
Hoffら,1996
Kauppら,1992
|
【出典】Bidlemann T.F., Harner T. (2000): Sorption to Aerosols. In Handbook of property estimation methods for chemicals: environmental and health sciences edited by Boethling R.S., Mackay D. CRC Press. |
さらに,Pankow(1987)が詳細に解説しているように,Yamasakiら(1982)はLangmuirの吸着等温式からKpの温度依存性について解析し,以下の式を導出しています。

ここで;
mY:同一物質に対し,異なる温度(T,単位:K)で測定されたKpの対数値と1/Tの直線回帰式の傾き。
bY:同様に,Kpの対数値と1/Tの直線回帰式の切片。
式(19)から,mY > 0であれば,温度上昇に従い,Kpは小さくなり,化学物質がガス態として空気中で存在する割合が大きくなります。これは,一般に,温度が上昇すると化学物質の蒸気圧(P0)が大きくなり,これに伴って,Junge式(式(2))の分母も大きくなり,φが小さくなることからも理解できます。
式(18)や式(19)による化学物質の大気中の浮遊粒子への分配やその温度による変化の予測は,すでに測定値があればモデル構築時に有用ですが,このような測定値は多くの化学物質でありません。したがって,基礎的な物性値によるスクリーニング的な化学物質の環境動態推定には,いささか上向きです。
前回解説したJunge式は,欧州連合(EU)の統一的リスク評価システムであるEUSES(European Union System for the Evaluation of Substances)のマルチメディアモデル(SimpleBoxモデル)で使用されています。一方,Junge式のような基礎物性値(蒸気圧)からKpを推定する既報の手法として,Mackayは彼の著書“Multimedia Environmental Models, The Fugacity Approach”内で2つの方法を推奨しています。以後,これらについて説明します。
3.Mackayらの吸着モデル
Mackayら(1986)は,無次元の粒子/空気分配係数(KQA)を化学物質の単位容積当りの浮遊粒子中濃度(Ca,p,単位:ng/m3)と空気中濃度(Ca,g,単位:ng/m3)の比として定義しています。このKQAとKpには以下の関係があります。

ここで;
VT:空気中の浮遊粒子の容積比。
Mackayらは,低揮発性物質の浮遊粒子への吸着を想定し,Yamasakiら(1982)が測定したベンゾ[a]アントラセンの分配データから,近似的に以下の式を得ています。

さらに,式(20)と式(21)から,TSPを100μg/m3,VTを5×10-11と仮定して,以下の式を得ています。

4.Pankowの吸収モデル
Pankow(1994)は浮遊粒子上の液状有機物の膜への化学物質の吸収・溶解として取り扱うことにより,Kpを式(22)で導出しています。

ここで;
fom:浮遊粒子上の化学物質を吸収する有機物膜の重量比。
MWom:化学物質を吸収する有機物の分子量。
γom:浮遊粒子上の有機物中における化学物質の活量係数。
Raoultの法則が成り立つ理想溶液では,以下の気液平衡の関係が成立します。

ここで;
Pi:気相中における化学物質 i の分圧。
Xi:液相中における化学物質 i のモル分率。
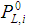 :化学物質iの飽和蒸気圧(固体の場合:過冷却液体の飽和蒸気圧)。
:化学物質iの飽和蒸気圧(固体の場合:過冷却液体の飽和蒸気圧)。
一方,Raoultの法則から外れる非理想溶液では,液相中の化学物質 i の活量係数(γi )を用い,式(23)は以下のように修正されます。

同様に,浮遊粒子上の液状有機物中と空気の間に式(25)で表される気液平衡が成立します。

ここで;
PL:気相中における化学物質の分圧。
Xom:浮遊粒子上の液状有機物膜中の化学物質のモル分率。
空気中の化学物質濃度(Ca,g,単位:ng/m3)は気体の状態方程式で計算できます。
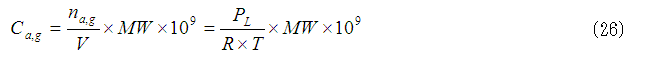
ここで;
na,g:空気中の化学物質のモル数(mole)。
V:空気の体積(単位:m3)。
MW:化学物質の分子量(g/mole)。
式(26)に式(25)を代入すると次式を得ます。

浮遊粒子上の液状有機物の全モル数(ntot,om)は式(28)で,液状有機物中の化学物質のモル数(np,om)は式(29)で求めることができます。


ここで;
Fp,om:浮遊粒子上の有機物膜に溶解している化学物質濃度(単位:ng/m3)。
モル分率(Xom)はnp,omとntot,omの比(np,om/ntot,om)ですから,上の2式から式(27)は以下のように改変できます。
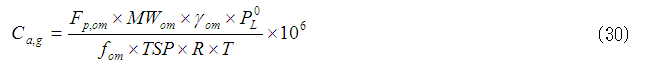
上記の式(30)から以下のように,Kpを式(22)として導出できます。
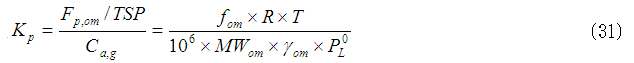
Finizoら(1997)は,さらに,オクタノール/空気分配係数(KOA)を導入して,式(31)で示されるKpと関係付けています。
式(31)の両辺を対数変換すると以下の式が得られます。
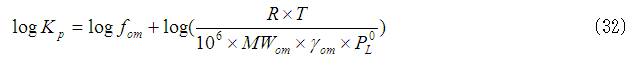
ここで,空気*オクタノール系での非理想溶液の気液平衡を考えます。KOAはオクタノール中の化学物質濃度を同じ単位の化学物質の空気中濃度で除した値で,上記の式(31)の導出過程と同様に考えることにより,式(33)で求めることができます。

ここで;
ρO:オクタノールの密度(820 kg/m3 @20℃)。
MWO:オクタノールの分子量(130 g/mole)。
γO:オクタノール中における化学物質の活量係数。
式(32)と式(33)から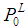 を消去すると,次式が得られます。
を消去すると,次式が得られます。

さらに,オクタノールと浮遊粒子上の有機物の分子量はほぼ等しいと仮定し,ρOに820 kg/m3を代入し,両辺を対数変換すると以下の式が得られます。
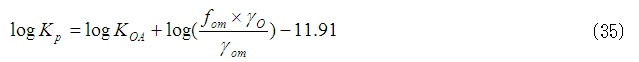
ここで,γO/γomの比があまり変動せず,両活量係数はほぼ等しく,都市域での測定結果から浮遊粒子が有機物を20%含むと仮定すると,式(35)はさらに簡略化され,以下の式で表されます。

この式(36)が式(21)とともに,Mackayが“Multimedia Environmental Models, The Fugacity Approach”で紹介している推算法です。
残念ながら,今回も実測値との比較にまで至りませんでした。次回をご期待下さい。
参考文献
Pankow, J.F. (1987): Review and comparative analysis of the theories on partitioning between the gas and aerosol
particulate phases in the atmosphere. Atmospheric Environment. 21: 2275-2283.
Pankow, J.F. (1994): An absorption model of gas/particle partitioning of organic compounds in the atmosphere. Atmospheric
Environment. 28: 158-188.
Finizio, A. et al. (1997): Octanol-air partition coefficient as predictor of partitioning of semi-volatile organic
chemicals to aerosols. Atmospheric Environment. 31: 2289-2296.
Bidleman, T.F., Harner, T. (2000): Sorption to Aerosols. In Handbook of property estimation methods for chemicals (edited
by Boethling RS, Mackay D). Lewis Publishers.
Mackay, D. (2001): Multimedia environmental models, The fugacity approach, 2nd Edition. Lewis Publishers.


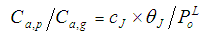 前回の解説,式(13)参照)ですので,KPはJunge定数(cJ)を用いて式(16)に示すように表されます。
前回の解説,式(13)参照)ですので,KPはJunge定数(cJ)を用いて式(16)に示すように表されます。

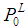 の対数値と傾き -1 の線形関係が得られます。
の対数値と傾き -1 の線形関係が得られます。

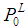 の間には以下の線形関係が成立すると報告されています。
の間には以下の線形関係が成立すると報告されています。







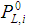 :化学物質iの飽和蒸気圧(固体の場合:過冷却液体の飽和蒸気圧)。
:化学物質iの飽和蒸気圧(固体の場合:過冷却液体の飽和蒸気圧)。