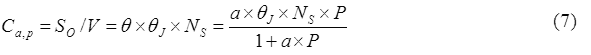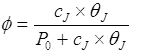第1回:大気中における動態(1)
第1回:大気中における動態(1)
大気浮遊粒子への吸着,Junge式の導出
1.はじめに
地圏や水圏と接する対流圏大気中には,土壌粒子の巻き上げのような自然発生源と工場やディーゼル車等から排出される人為発生源からの様々な浮遊粒子が存在します。一般に,燃焼に伴って排出される粒子状炭素や排気ガス中の微粒子に加えて,SOxやNOx等のガス状物質が大気中で化学反応等により低蒸気圧物質に変化し粒子化した二次粒子を微小粒子と呼び,これらの微小粒子のほとんどは人為起源と考えられています。
今回は,大気中浮遊粒子への化学物質の吸着について考えます。ガス態または粒子吸着態として大気中に存在する化学物質は異なる動態を示しますので,浮遊粒子への吸脱着の過程は化学物質の大気中での動態を考える上で,最初に明確にする必要があります。
2.Junge式
一定の容積の大気中にガス状物質として存在する化学物質の濃度をCa,g(単位:mg/m3),浮遊粒子に吸着された化学物質の濃度をCa,p(単位:mg/m3)とした場合,大気中の浮遊粒子に吸着されている化学物質の割合(φ)は,式(1)で定義されます。

Junge式はこの(φ)を以下の式で推定します。

ここで;
cJ : Jungeの定数。Jungeは化学物質により変わらないとし,17 Pa/cmとしています。
θJ : 浮遊粒子の全表面積。Jungeは都市域で約3×10-6~3×10-5 cm2/cm3程度と報告していますが,Bidlemanは米国の都市域に対し,1.1×10-5 cm2/cm3としています。
P0 : 化学物質の飽和蒸気圧。固体物質に対しては,その物質の過冷却液体状態の蒸気圧(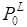 ,単位:Pa)を使用します。この
,単位:Pa)を使用します。この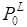 は,固体物質の飽和蒸気圧(
は,固体物質の飽和蒸気圧(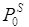 ,単位:Pa)を用いて,以下の式で計算できます。
,単位:Pa)を用いて,以下の式で計算できます。

ここで;
Tm : 融点(単位 : K)
T : 気温(単位 : K)
ΔSf : 融解エントロピー。ΔSf/R(Rは気体定数)として6.79が一般に使用されます。
3.Junge式の導出
Junge式は大気中でのガス態と浮遊粒子吸着態の存在比率を推定するのに一般的に用いられる式ですが,どのようにして導出されたかについては知らない方も多いようです。今回は,この導出課程をメインに解説します。
一般に,大気中の浮遊粒子の固体表面に化学物質が吸着される場合,以下の2つのメカニズムが考えられます。
・物理吸着 : 固体(吸着剤)の表面と吸着される分子の間に,van der Waals力のような分子間力が作用することに起因します。可逆的な吸着過程です。
・化学吸着 : 固体(吸着剤)の表面と吸着される分子の間に化学結合が生じることに起因します。上可逆的な吸着過程です。
3.1 吸着等温式
ガス状物質の吸着は一定温度下で,一定量の吸着剤に吸着されるガス状物質量とその際の圧の関係を測定することにより調べられ,結果は吸着等温線として表されます。そして,気相の化学物質の吸着の場合には,吸着現象を表す吸着等温式として,Langmuirの式やBET(Brunauer-Emmett-Teller)式が適用されます。
Langmuirの吸着等温式(式(4))は,以下の仮定の下に導出されます。
1) 固体の表面は均一で分子の吸着活性点は決まっており,吸着のエネルギーも全て等しい。
2) 吸着された分子の間に相互作用は生じない。
3) 吸着活性点が分子に占有されると吸着能は消失し,多分子層吸着は生じない。

この式(4)において;
P : 吸着平衡が成立した時の化学物質の平衡分圧(単位:Pa)。
SOとST : 平衡分圧Pにおいて,化学物質により占有された吸着活性点のモル数(SO)と全吸着活性点のモル数(ST)。
これらの比(SO/ST)は被覆率(θ)と呼ばれます。
a : 吸着速度定数(kad)と脱着速度定数(kd)の比(kad/kd)に相当します。
実験的に,1/SOと1/Pの間に直線関係が成立すれば,Langmuirの吸着等温式を導出する際の仮定が成立し,切片から1/STが,傾きから1/(a×ST)を求めることができます。
一方,BET(式(5))は,以下の仮定の下に導出されます。
1) 固体の表面は均一で分子の吸着活性点は決まっており,吸着のエネルギーも全て等しい。
2) 吸着された分子の間に相互作用は生じない。
3) 化学物質分子は多分子層に無限に吸着できる。
4) 第1層から第n層までの各吸着層でLangmuirの吸着等温式が成立する。
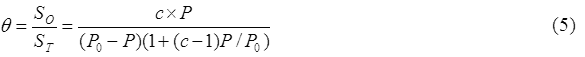
ここで;
c : 固体表面と吸着分子間の相互作用の程度を示す定数。
P0 : 吸着される化学物質の飽和蒸気圧。
平衡分圧Pが非常に低い場合,Langmuirの吸着等温式とBET吸着等温式において,被覆率(θ)はそれぞれ,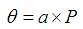 と
と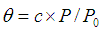 となり,両吸着等温式の定数aとcの間には,a=c/P0の関係が成立します。
となり,両吸着等温式の定数aとcの間には,a=c/P0の関係が成立します。
3.2 環境大気中の化学物質の浮遊粒子への吸着
環境大気中の化学物質の動態を推定する際に必要なのは,大気中にガス態および浮遊粒子吸着態として存在する化学物質の比率ですが,式(4)と式(5)から直接求めることはできません。そこで,大気中の化学物質がガス態および浮遊粒子吸着態として存在する割合を推定できる式をLangmuirの吸着等温式から導出します。
Langmuirの吸着等温式の被覆率(θ)は,式(6)のように書き直すことができます。

ここで;
V : 空気の容積。
θJ : 2節に示した単位容積当たりの空気中の浮遊粒子の表面積
NS :浮遊粒子の単位表面積当たりの吸着活性点のモル数です。
Langmuirの吸着等温式では単分子層への吸着を仮定しますので,浮遊粒子に吸着された化学物質の濃度(Ca,p)はS0/Vと等しくなり,式(7)のように書き直すことができます。
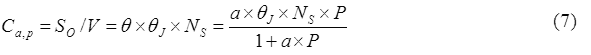
一方,ガス態として存在する化学物質の濃度(Ca,g)は平衡分圧Pから,理想気体を仮定して,式(8)で計算されます。

したがって,空気中の浮遊粒子に吸着された化学物質濃度とガス態として存在する化学物質の濃度比(Ca,p/Ca,g)は式(9)で,浮遊粒子に吸着される割合(φ)は式(10)で与えられます。


さらに,平衡分圧が非常に低い状況(1 » a×P)では,式(9)と式(10)は以下の2式で近似できるようになります。


Jungeは,BET式からφを導出することを試み,その際に,a » 1(すなわち,kad »kd)そして,P<<P0(すなわち,θ<1)という条件を仮定しました。この条件下では,3.1節に示したようにBET式とLangmuir式の定数には,a=c/P0の関係が成立します。この式を式(11)と式(12)に代入することにより,以下の2式が得られます。


さらに,Jungeはc×R×T×NSを定数cJ(Jungeの定数)としてまとめました。これにより,式(14)は以下のJunge式(2)が導出されます。
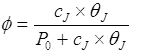
3.1節に説明しましたが,cJはBET式の定数c,温度Tおよび浮遊粒子の単位表面積当たりの吸着サイトのモル数NSの関数でこれらの値より変化しますが,JungeはcJ=17 Pa/cmで変化しないと仮定しています。
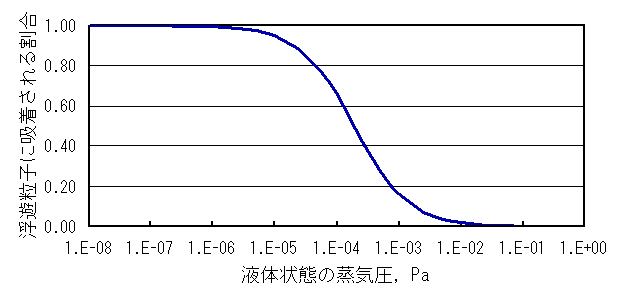
以下の図は,化学物質の液体状態での飽和蒸気圧が10-8 ~1 Paの範囲において,Junge式(式(2))で計算された大気中の浮遊粒子に吸着されている化学物質の割合(φ)を示しています。計算に際しては,Jungeの定数(cJ)を17 Pa/cm,浮遊粒子の全表面積(θJ)を1.1×10-5 cm2/cm3としています。図から明らかなように,液体状態での蒸気圧が10-5 Pa以下の化学物質の場合,大気中の浮遊粒子にほぼ全量が吸着された状態で存在し,逆に0.01 Pa以上であれば,ほぼガスとして存在することがわかります。
参考文献
Pankow, J.F. (1987): Review and comparative analysis of the theories on
partitioning between the gas and aerosol particulate phases in the
atmosphere. Atmospheric Environment. 21: 2275-2283.


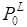 ,単位:Pa)を使用します。この
,単位:Pa)を使用します。この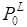 は,固体物質の飽和蒸気圧(
は,固体物質の飽和蒸気圧(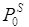 ,単位:Pa)を用いて,以下の式で計算できます。
,単位:Pa)を用いて,以下の式で計算できます。


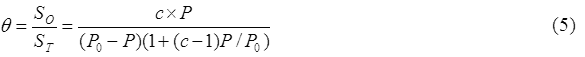
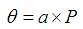 と
と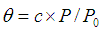 となり,両吸着等温式の定数aとcの間には,a=c/P0の関係が成立します。
となり,両吸着等温式の定数aとcの間には,a=c/P0の関係が成立します。