一様分布

　確率変数の値の如何に関わらず確率密度関数が一定の値をとるような分布を一様分布と呼び、不確かさ評価のときにしばしば出てくる重要な分布の一つです。通常、変数の値は限られており、たとえば下限がで上限がとすると、確率の総和は1になるという制約から、確率密度関数は

すなわち

となります。

　一様分布の期待値は、上図の矩形の面積の総和であるから

となります。

また、一様分布の分散は上図の影を付けた部分の総面積だから、からまでの斜線の面積を２倍したものになります。すなわち

となります。あるいは、もっと簡単に、連続的な分散の公式

を用いることによっても次の通り一様分布の分散が求められます。

また、一様分布の標準偏差は

となります。

一様分布を使わなければならない卑近な例は、たとえばある分析装置の検出限界がで、それ以下の濃度の物質量（たとえば不純物の濃度）を測定しようとしてもその測定値に意味がなく、不純物の濃度は高々であるとしか言えない場合、不純物の不確かさをこの一様分布を使って見積もることになります。すなわち、検出限界以下の不純物濃度の標準不確かさは理論的には濃度0から検出限界までのどこかに分布しているはずであり、不純物濃度0と検出限界の中間点の濃度を不純物濃度の平均値とみなし、不純物濃度0から検出限界までの区間を一様分布と考えることにより、不純物濃度の標準不確かさは

となります。

　母集団分布が一様分布

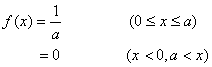
であるような母集団からの標本が(1.5, 0.4, 0.9, 2.0,1.3, 0.7)であったとき、その一様分布の母平均を区間推定（危険率）するには次のようにします。標本データをそれぞれ

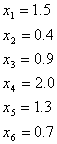
と定義する。ここで標本数はであり、一様分布に従う確率変数の実現値の最大値は

です。一様分布の区間の上限を区間推定すると

となります。したがって、一様分布の母平均の信頼区間は

となります。

（実例）正規分布を仮定するには測定データの数が少なくデータに十分な信頼性がもてない場合の純度の不確かさ

　いまある物質の純度を２回測定した結果が99.8052%と99.816%であったとき、その２つの測定値は、純度の下限と上限（純度は100%を超えることはあり得ないから）の範囲内にある一様分布の区間中に落ちるものとみなし、純度の標準不確かさは一様分布の母平均、すなわち

と上限の値を使って母分散を算出し、下記のように、求めることができます。