母数型と変量型の要因効果（母数因子と変量因子）
要因効果には、母数型と変量型があり、そのような主効果を観測データに与える因子をそれぞれ母数因子および変量因子と呼んでいます。
１）母数型
因子の各水準における主効果がそれぞれ一定の値をとる要因効果を「母数型」と呼び、主効果が母数型である因子を「母数因子」と呼んでいます。すなわち、母数因子（たとえば因子A）においては、その各水準Aiごとの母平均μi がどのような値をとるかに主たる関心があり、また、母平均μi がμi の平均値μから常に一定の差αi （αi = μi – μ）を持つことと、各水準の効果αiの総和が0であること（
）が特徴です。このあたりの事情を説明するために、因子Aの水準数が２であるデータ構造を図示すると、
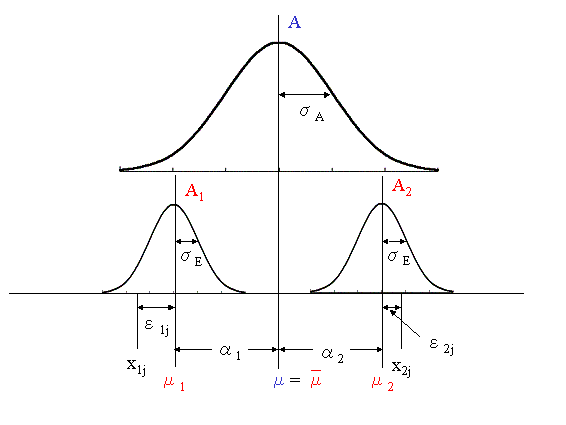
のように、水準A1の平均μ1と水準A2の平均μ2の平均
は水準Aの母平均μと一致します。したがって
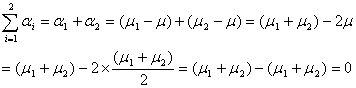
から類推できるように、母数因子の場合は常に
となります。また、
の母集団である因子Aの分散
は水準数をnとすれば
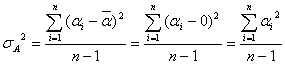
となります。
２）変量型
要因効果がある確率分布に従う確率変数とみなされるような場合を「変量型」と呼び、主効果が変量型である因子を「変量因子」と呼んでいます。たとえば、因子Aが変量因子である場合は、次図
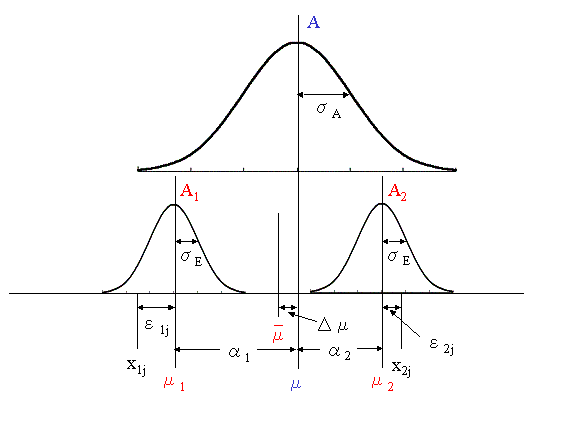
に示されるように、母平均μの周りに
という母分散を持つ要因効果の母集団を考えることができ、ある水準Aiの効果
は、その母集団から無作為に選び出されたことを意味します。したがって、どのような水準が選び出されるかはあなたまかせであるので、実際に選び出されたいくつかの水準の母平均μiを平均（
）してみても、μに一致するとは限らず、一般に
となります。
また、変量因子の場合は、
において母平均μは一定であっても
はランダムに変わり得るので、要因効果
も、母数因子のように一定値ではなく、ランダムに変わり得ることになります。すなわち、一般的に
となります。もちろん、無限回にわたって無作為抽出を行いその効果
を平均すれば、その期待値は
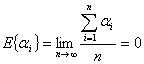
のように0になります。また、水準
の効果
の分散は、その水準数をnとすれば
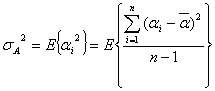
のようになります。
母数因子が母集団そのものよりも各水準間の母平均に主たる関心があるのに対して、変量因子では各水準の母平均の比較には何の意味も持たないが、それが選ばれたもとの母集団の特性値（分散成分など）に主たる関心がある場合に変量型が適用されます。したがって、春夏秋冬の雨量測定など季節変動を調べる場合は母数型となりますが、「完全無作為抽出」は変量型の典型例となります。