t分布の逆関数表

 

　下表は危険率すなわちとすなわち点のスチューデント分布の逆関数との値を示しています。この値はMicrosoftの表計算ソフトExcelを使えば簡単に求められます。すなわち、Excelのツールバーメニューの中の「」（関数の貼り付け）を選び、さらに「関数の分類」で「統計」を、「関数名」で「TINV」を選べば、「確率」すなわち危険率の値と「自由度」の値の入力を要求されるので、それらの値を入力すれば、下表のようなスチューデント分布の確率密度関数の逆関数との値が簡単に得られます。ただし、Excelの「TINV」関数は確率の値として、いつも「両側検定」（）の危険率の値の入力を前提としているので、「片側検定」（）の場合は「TINV」関数の確率の入力値としてはの値を入力しなければなりません。スチューデント分布の確率密度関数は自由度によって関数の形状は変わりますが、の極限では標準正規分布の確率密度関数に一致します。

 

 

　一般に母集団の母平均と母分散は未知であるので、この母集団から無作為抽出した標本の標本平均と不偏分散あるいはを使って母平均の点推定値あるいは区間推定量を求めるのが普通です。ここで、は信頼区間（confidence interval）と呼ばれるものであり、はあるいはの平方根の比例関数となっていますが、その比例定数に相当するものがスチューデントの分布の逆関数の値で定義されます。このは「不確かさ」の分野では「拡張不確かさ」に相当し、スチューデント分布の逆関数の値は包含係数の値に相当するものです。また、は「標準不確かさ」に相当します。したがって、大きさの標本（したがって、通常は自由度）について、*分布を使って母平均を確率の信頼水準で区間推定すると

 

               

 

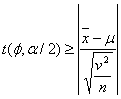
のようになるので、母平均の確率での信頼区間は

 

             

 

のような両側検定によって求めることができます。ここで、は大きさの標本の不偏分散であり、母分散の推定値に相当します。すなわち

 

               

 

です。たとえば、正規分布の（２シグマ）にほぼ相当する確率すなわちの信頼水準で母平均の区間推定を行いたい場合には、標本についての不偏分散を求めた後、標本の大きさに相当する自由度に対応する危険率のを下表から求め、次式

 

               

 

あるいは

 

   

 

にを代入すれば求める答えが得られます。

 

信頼水準 (%)

95%

正規分布の2シグマ相当（95.45%）

正規分布の3シグマ相当（99.73%）

検定方式

片側検定

両側検定

片側検定

両側検定

　片側検定

両側検定

信頼水準

1-α=0.95

1-2×(α/2)=1-α=0.95

1-α=0.9545

1-2×(α/2)=1-α=0.9545

1-α=0.9973

1-2×(α/2)=1-α=0.9973

危険率

α=0.05

α/2=0.025

α=0.0455

α/2=0.02275

α=0.0027

α/2=0.00135

φ（自由度）

t(φ,α)

t(φ,α/2)

t(φ,α)

t(φ,α/2)

t(φ,α)

t(φ,α/2)

1

6.3137

12.7062

6.9481

13.9678

117.8868

235.7736

2

2.9200

4.3027

3.0843

4.5266

13.5531

19.2062

3

2.3534

3.1824

2.4584

3.3068

7.2565

9.2189

4

2.1318

2.7765

2.2162

2.8693

5.4797

6.6200

5

2.0150

2.5706

2.0891

2.6487

4.6869

5.5070

6

1.9432

2.4469

2.0112

2.5165

4.2467

4.9040

7

1.8946

2.3646

1.9587

2.4288

3.9689

4.5299

8

1.8595

2.3060

1.9208

2.3664

3.7785

4.2765

9

1.8331

2.2622

1.8923

2.3198

3.6401

4.0942

10

1.8125

2.2281

1.8701

2.2837

3.5352

3.9570

11

1.7959

2.2010

1.8522

2.2549

3.4530

3.8499

12

1.7823

2.1788

1.8376

2.2314

3.3868

3.7643

13

1.7709

2.1604

1.8254

2.2118

3.3325

3.6941

14

1.7613

2.1448

1.8150

2.1953

3.2870

3.6358

15

1.7531

2.1315

1.8061

2.1812

3.2485

3.5864

16

1.7459

2.1199

1.7984

2.1689

3.2154

3.5441

17

1.7396

2.1098

1.7917

2.1583

3.1867

3.5074

18

1.7341

2.1009

1.7857

2.1489

3.1615

3.4754

19

1.7291

2.0930

1.7804

2.1405

3.1393

3.4472

20

1.7247

2.0860

1.7757

2.1330

3.1196

3.4221

21

1.7207

2.0796

1.7714

2.1263

3.1018

3.3997

22

1.7171

2.0739

1.7676

2.1202

3.0859

3.3795

23

1.7139

2.0687

1.7641

2.1147

3.0715

3.3613

24

1.7109

2.0639

1.7609

2.1097

3.0584

3.3448

25

1.7081

2.0595

1.7579

2.1051

3.0464

3.3296

26

1.7056

2.0555

1.7552

2.1009

3.0354

3.3157

27

1.7033

2.0518

1.7527

2.0969

3.0253

3.3030

28

1.7011

2.0484

1.7504

2.0933

3.0160

3.2913

29

1.6991

2.0452

1.7483

2.0900

3.0073

3.2804

30

1.6973

2.0423

1.7463

2.0868

2.9993

3.2703

31

1.6955

2.0395

1.7444

2.0839

2.9918

3.2609

32

1.6939

2.0369

1.7426

2.0812

2.9848

3.2521

33

1.6924

2.0345

1.7410

2.0787

2.9783

3.2440

34

1.6909

2.0322

1.7395

2.0763

2.9722

3.2363

35

1.6896

2.0301

1.7380

2.0740

2.9664

3.2291

36

1.6883

2.0281

1.7367

2.0719

2.9610

3.2223

37

1.6871

2.0262

1.7354

2.0699

2.9559

3.2159

38

1.6860

2.0244

1.7341

2.0680

2.9511

3.2099

39

1.6849

2.0227

1.7330

2.0662

2.9465

3.2042

40

1.6839

2.0211

1.7319

2.0645

2.9422

3.1987

41

1.6829

2.0195

1.7308

2.0628

2.9381

3.1936

42

1.6820

2.0181

1.7299

2.0613

2.9342

3.1888

43

1.6811

2.0167

1.7289

2.0598

2.9305

3.1841

44

1.6802

2.0154

1.7280

2.0584

2.9269

3.1797

45

1.6794

2.0141

1.7271

2.0571

2.9236

3.1755

46

1.6787

2.0129

1.7263

2.0558

2.9204

3.1715

47

1.6779

2.0117

1.7255

2.0546

2.9173

3.1677

48

1.6772

2.0106

1.7248

2.0534

2.9143

3.1640

49

1.6766

2.0096

1.7241

2.0523

2.9115

3.1605

50

1.6759

2.0086

1.7234

2.0513

2.9089

3.1571

51

1.6753

2.0076

1.7227

2.0502

2.9062

3.1539

52

1.6747

2.0066

1.7221

2.0492

2.9038

3.1508

53

1.6741

2.0057

1.7215

2.0483

2.9014

3.1479

54

1.6736

2.0049

1.7209

2.0474

2.8991

3.1450

55

1.6730

2.0040

1.7203

2.0465

2.8969

3.1422

56

1.6725

2.0032

1.7198

2.0456

2.8948

3.1396

57

1.6720

2.0025

1.7192

2.0448

2.8927

3.1370

58

1.6716

2.0017

1.7187

2.0440

2.8907

3.1346

59

1.6711

2.0010

1.7182

2.0433

2.8888

3.1322

60

1.6706

2.0003

1.7177

2.0425

2.8870

3.1299

61

1.6702

1.9996

1.7173

2.0418

2.8852

3.1277

62

1.6698

1.9990

1.7168

2.0411

2.8835

3.1255

63

1.6694

1.9983

1.7164

2.0405

2.8818

3.1235

64

1.6690

1.9977

1.7160

2.0398

2.8802

3.1215

65

1.6686

1.9971

1.7156

2.0392

2.8787

3.1196

66

1.6683

1.9966

1.7152

2.0386

2.8772

3.1177

67

1.6679

1.9960

1.7148

2.0380

2.8757

3.1159

68

1.6676

1.9955

1.7145

2.0374

2.8743

3.1141

69

1.6672

1.9949

1.7141

2.0369

2.8729

3.1124

70

1.6669

1.9944

1.7138

2.0363

2.8716

3.1108

71

1.6666

1.9939

1.7134

2.0358

2.8703

3.1091

72

1.6663

1.9935

1.7131

2.0353

2.8690

3.1076

73

1.6660

1.9930

1.7128

2.0348

2.8678

3.1060

74

1.6657

1.9925

1.7125

2.0344

2.8666

3.1046

75

1.6654

1.9921

1.7122

2.0339

2.8655

3.1031

76

1.6652

1.9917

1.7119

2.0334

2.8643

3.1017

77

1.6649

1.9913

1.7116

2.0330

2.8632

3.1004

78

1.6646

1.9908

1.7113

2.0326

2.8621

3.0990

79

1.6644

1.9905

1.7110

2.0321

2.8611

3.0977

80

1.6641

1.9901

1.7108

2.0317

2.8601

3.0965

81

1.6639

1.9897

1.7105

2.0313

2.8591

3.0953

82

1.6636

1.9893

1.7103

2.0310

2.8581

3.0940

83

1.6634

1.9890

1.7100

2.0306

2.8572

3.0929

84

1.6632

1.9886

1.7098

2.0302

2.8563

3.0918

85

1.6630

1.9883

1.7095

2.0298

2.8554

3.0907

86

1.6628

1.9879

1.7093

2.0295

2.8545

3.0896

87

1.6626

1.9876

1.7091

2.0291

2.8537

3.0885

88

1.6624

1.9873

1.7089

2.0288

2.8529

3.0875

89

1.6622

1.9870

1.7087

2.0285

2.8520

3.0865

90

1.6620

1.9867

1.7084

2.0282

2.8513

3.0855

91

1.6618

1.9864

1.7082

2.0279

2.8505

3.0845

92

1.6616

1.9861

1.7080

2.0275

2.8497

3.0836

93

1.6614

1.9858

1.7079

2.0272

2.8490

3.0827

94

1.6612

1.9855

1.7077

2.0269

2.8482

3.0817

95

1.6611

1.9852

1.7075

2.0267

2.8475

3.0809

96

1.6609

1.9850

1.7073

2.0264

2.8468

3.0800

97

1.6607

1.9847

1.7071

2.0261

2.8462

3.0792

98

1.6606

1.9845

1.7069

2.0258

2.8455

3.0783

99

1.6604

1.9842

1.7068

2.0256

2.8448

3.0775

100

1.6602

1.9840

1.7066

2.0253

2.8442

3.0767

 

 

（参考）正規分布の（２シグマ）に対応する確率は正確にはすなわちですから、正規分布の（２シグマ）対応で両側検定する場合には、スチューデント分布の逆関数の値を求めるために入力する値はにする必要があります。同様に、正規分布の（３シグマ）に対応する確率は正確にはすなわちですから、正規分布の（３シグマ）対応で両側検定する場合のスチューデント分布の逆関数の値を求めるために入力する値はにする必要があります。