t分布

t 分布

分布（t-distribution）はStudentの分布とも呼ばれ、推測統計学では非常に重要な分布の一つです。いま、互いに独立な２つの変数とがあって、は標準正規分布型分布をし、は自由度の分布をするものとします。このとき、次式で与えられる変数との結合変数は標本平均について自由度の分布をすることがStudentというペンネームをもつ統計学者（W. S. Gosset）によって見い出されました。

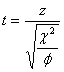
　この自由度の分布の確率密度関数は次式で与えられます。

あるいは

ここで、は次式で与えられるベータ関数です。

また、やなどはガンマ関数と呼ばれ、次のような性質があります。

１）

２）

３）

４）

５）

分布は分布と同じように自由度によってその形は変わるが、を中心にして左右対称であり、自由度で標準正規分布に一致します。

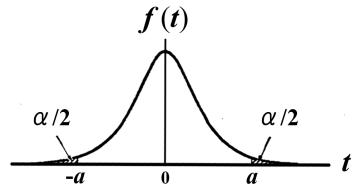
　分布において、があるの値より大きくなる確率は理論的に次式から求められ、この値を表にしたものが分布です。

ここで、は中の条件下での確率です。

　分布の期待値と分散は

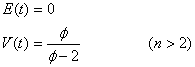
となります。ただし、では分散は無限大に発散してしまうため存在しません。

　また、の特殊な場合には、分布は

となりますが、これはコーシー分布（Cauchy distribution）あるいはローレンツ曲線（Lorenzian curve）と呼ばれる関数となります。コーシー分布を一般化した記号はで表され、その密度関数は

となり、下図のような形状の曲線になります。

　コーシー分布には期待値と分散は存在しないことと、コーシー分布には中心極限定理が適用できないことには注意する必要があります。

　互いに独立に標準正規分布に従う確率変数の比はコーシー分布に従います。すなわち

となります。また、がの一様分布に従うとき、はコーシ分布になります。すなわち

となります。

　正規母集団から大きさのランダム標本を抽出し、その平均について規準化変数を

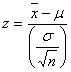
のように表せば、この規準化変数は標準正規分布型分布をします。

　一方、は自由度の分布をするから、

分布に従うこのの式を上述の標準正規分布に従うの式と比較すると、の式はの式の母標準偏差を標本の不偏標準偏差で置き換えたものになっています。したがって、このの式には正規母集団の母数である母平均のみしか含まないので、分布は母平均を推定するのに適切で重要な分布です。

これに対し、分布は

の式から明らかなように、正規母集団の母数である母分散のみしか含まないので、母分散を推定するのに適切で重要な分布として知られています。

　個の標本からなる分布を使って母平均を確率の信頼限界で区間推定すると

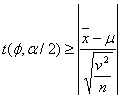
のようになるので、母平均の確率での信頼区間は

のような両側検定によって求めることができます。

　分布の特徴から次のような重要な定理が導かれます。すなわち、分散の等しい２つの正規母集団とからそれぞれ独立に大きさの任意標本を抽出し、それぞれの標本平均を、不偏分散をとすれば

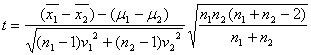
は自由度の分布をするという定理です。この定理の根幹をなす部分は２つの母分散が等しいという「等分散の条件」ですが、現実の正規母集団においては等分散の条件が満たされる場合が多いこととたとえ多少満たされなくても上式が分布からはずれることが少ないという理由から、２つの正規母集団の比較検定や推定に利用されること多い重要な定理です。