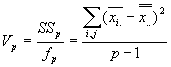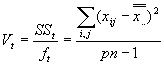データ構造による総平均の不確かさの違い
1)すべてのデータが与えられている場合
すべてのデータが1つの母集団を形成している場合の平均と分散を![]() と
と![]() と定義し、また、これらのデータを
と定義し、また、これらのデータを![]() 個のグループ(ただし各グループにはデータがそれぞれ
個のグループ(ただし各グループにはデータがそれぞれ![]() 個ずつあるものとする)に分けた時のそれぞれの母集団の平均を
個ずつあるものとする)に分けた時のそれぞれの母集団の平均を![]() および分散を
および分散を![]() とします。また、個々のデータはグループ分けした場合を考慮して
とします。また、個々のデータはグループ分けした場合を考慮して![]() の記号で表記します。したがって、総平均
の記号で表記します。したがって、総平均![]() は
は

となります。また、総分散![]() は次のように定義されます。
は次のように定義されます。
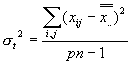
一方、![]() 個にグループ分けされたデータ群をそれぞれ
個にグループ分けされたデータ群をそれぞれ![]() 個の繰り返し観測データだとして、一元配置の分散分析を行い、その級間不偏分散を
個の繰り返し観測データだとして、一元配置の分散分析を行い、その級間不偏分散を![]() 、また級内不偏分散を
、また級内不偏分散を![]() とする。ここで、級間変動の分散を
とする。ここで、級間変動の分散を![]() 、また級内変動の分散を
、また級内変動の分散を![]() とおけば、
とおけば、
![]()
![]()
となります。
不偏分散![]() および
および![]() は
は


と定義されますので、上述の総分散![]() の式を次のように書き表すことができます。
の式を次のように書き表すことができます。
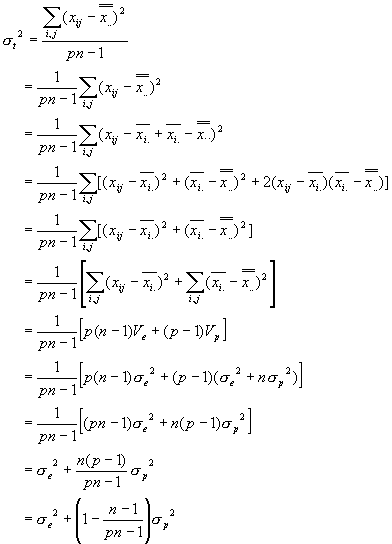
したがって、総平均![]() の標準不確かさの2乗
の標準不確かさの2乗![]() は
は
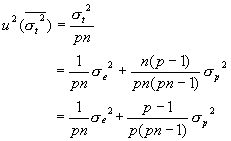
となります。
一方、グループ分けして一元配置の分散分析より求められる総平均![]() の標準不確かさの2乗
の標準不確かさの2乗![]() は
は
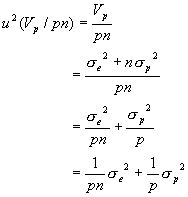
となります。
総平均![]() の標準不確かさの2乗に関しては、1つの母集団としてデータの処理を行うか、またはグループ分けしたデータを一元配置の分散分析で処理するかの違いにより、下記のような差違
の標準不確かさの2乗に関しては、1つの母集団としてデータの処理を行うか、またはグループ分けしたデータを一元配置の分散分析で処理するかの違いにより、下記のような差違![]() が生ずることになるが、その差はもし級間変動に起因する分散
が生ずることになるが、その差はもし級間変動に起因する分散![]() が0であれば、総平均
が0であれば、総平均![]() の標準不確かさの2乗は両定義で一致し、
の標準不確かさの2乗は両定義で一致し、![]() となります。
となります。

上式から差違![]() は、
は、![]() が大きければ
が大きければ![]() に近似でき、また
に近似でき、また![]() がかなり大きい場合は無視し得るほどその値は小さくなり、極限的には総平均
がかなり大きい場合は無視し得るほどその値は小さくなり、極限的には総平均![]() の標準不確かさの2乗
の標準不確かさの2乗![]() は偶然誤差に起因する成分
は偶然誤差に起因する成分![]() のみになります。
のみになります。
BIPMのCCQMデータベースの基幹比較などにおいては、総平均![]() (CCQMでは
(CCQMでは![]() で表示されている)の標準不確かさ
で表示されている)の標準不確かさ![]() (CCQMでは
(CCQMでは![]() で表示されている)は、上述のグループ分けした一元は位置の分散分析によって定義される値
で表示されている)は、上述のグループ分けした一元は位置の分散分析によって定義される値
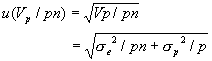
が用いられています。
グループ分けしたデータの一元配置分散分析表(ANOVA)
|
偏差平方和 |
自由度 |
不偏分散(平均平方) |
期待値 |
|
級間変動 |
|
|
|
|
級内変動 |
|
|
|
|
総変動 |
|
|
|
2)グループ分けした各グループの平均![]() のみがわかっている場合
のみがわかっている場合
文献などで報告されているデータには個々のデータのすべてが記載されておらず、断片的なデータのみから総平均![]() の標準不確かさ
の標準不確かさ![]() を求めたい場合があります。いま、個々のデータはわからないがグループ分けした各グループの平均値
を求めたい場合があります。いま、個々のデータはわからないがグループ分けした各グループの平均値![]() だけがわかっている場合について、その標準不確かさ
だけがわかっている場合について、その標準不確かさ![]() を求めてみることにします。
を求めてみることにします。
総平均![]() は、各グループの平均
は、各グループの平均![]() の算術平均であるから
の算術平均であるから
![]()

となります。また、求めるべき総平均![]() の標準不確かさ
の標準不確かさ![]() の2乗
の2乗![]() は、各グループの平均
は、各グループの平均![]() の標本から得られる不偏分散
の標本から得られる不偏分散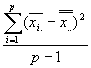 を平均したものであるから
を平均したものであるから
![]()

となります。そこでこの式をさらに変形すると
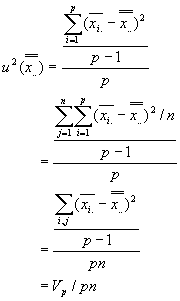
となり、これはグループ分けして一元配置の分散分析より求められる総平均![]() の標準不確かさの2乗
の標準不確かさの2乗![]() と一致します。
と一致します。
3)グループ分けした各グループの平均![]() の標準不確かさ
の標準不確かさ![]() のみがわかっている場合
のみがわかっている場合
このような場合には、総平均![]() は、各グループの平均
は、各グループの平均![]() の算術平均であるから
の算術平均であるから
![]()

となるので、これを![]() と置き、
と置き、![]() について不確かさの伝搬即を適用すれば
について不確かさの伝搬即を適用すれば

![]()
となります。上式の右辺の![]() は、各グループの標本平均
は、各グループの標本平均![]() の不偏分散
の不偏分散 の平均値である、すなわち
の平均値である、すなわち
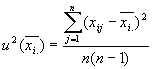
であるから、
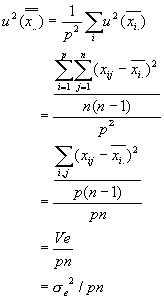
となり、これは1)で検証したように、グループ間変動の分散![]() が0の場合と合致しますから、グループ間変動の分散
が0の場合と合致しますから、グループ間変動の分散![]() が小さいかグループ数
が小さいかグループ数![]() がかなり大きい時にはよい近似値となります。
がかなり大きい時にはよい近似値となります。