安定性保証期間の保証値の不確かさ

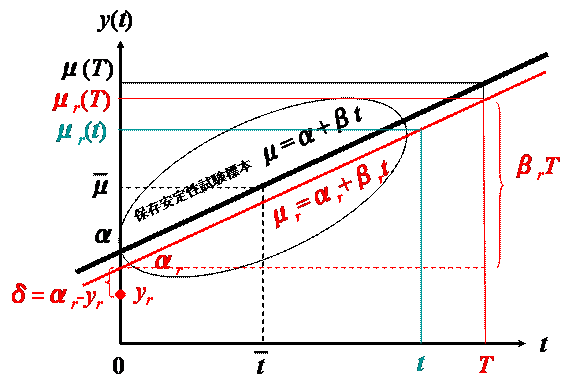
ある時点（時間）で調製した特定標準溶液の濃度の認証値（保証値）をとすると

なるモデル式で表すことができます。ただし、この濃度の時間後の濃度の真の値は

のような回帰直線モデル（切片、傾き）で表せるものとします。すると時刻における濃度の不確かさ（誤差）は

となります。したがって、その誤差分散は保証期間（）内でいつその標準溶液がユーザーに使われるかわからないので、その時間平均とすれば

となります。また保証期間ぎりぎりいっぱいまでの濃度値（）まで保証するとすれば（すなわちほとんどのユーザーは常に時刻で標準溶液を使うものとすれば）

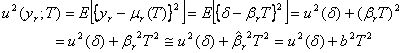
となります。ここで、簡単のために

としたが、正確には回帰係数には

なる誤差があるので

となるが、一方で繰り返しのある回帰直線近似ではその回帰係数の母数に関して

なる関係が成り立つことが統計学でよく知られています。

ここで、時刻における濃度の不確かさ（誤差）は

であることをすでに導いたので、この式に上述の関係式を適用すると

となります。すなわち、誤差は時刻の関数でありしかも直線近似（傾きでその誤差は）の関数となっているので

回帰係数の最大値としては

と表現できます。したがっては

と表すことができます。よって、その誤差分散は保証期間（）内でいつその標準溶液がユーザーに使われるかわからないので、その時間平均とすれば

となります。また保証期間ぎりぎりいっぱいまでの濃度値（）まで保証するとすれば（すなわちほとんどのユーザーは常に時刻で標準溶液を使うものとすれば）

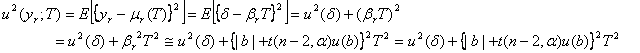
となります。これら2つの式のの項にはにはスチューデントのが掛かっているが、上式から求められるのは標準不確かさあるいはなので、それらの拡張不確かさやを求める際にはまたスチューデントのまたは適当な包含係数を掛けることになるので、過大評価しないため上式２つは

としておく方がよいと考えられます。

ただし、これら回帰係数およびその推定値として標本回帰係数を、また標本回帰係数の標準誤差（標準不確かさ）としてを用いたが、これら標本の回帰係数や不確かさは、安定性保証期間内で予め測定した標本データの真の値の回帰直線モデル式

の母回帰係数の推定値およびその不確かさから算出したもので近似することにします。

一方、直線回帰の検定でとはならないが、標本回帰係数がたまたま

となるような場合やもともと少ない標本データから得られた標本回帰分析の検定からでしかもであったとしても本当の母回帰直線が得られたならではあり得ないと考えられるような場合には、

のような誤差がの周りに分布していると考えられるので、時刻における標準溶液の濃度の不確かさ（誤差）の分散は

となります。

したがって、このような特殊な場合（直線回帰性はあるらしいが標本回帰係数がである場合）の特定標準溶液の認証値（保証値）は保証期間内の時間平均に対しては

であり、また保証期間ぎりぎりいっぱいまでの濃度値（）に対しては

となります。