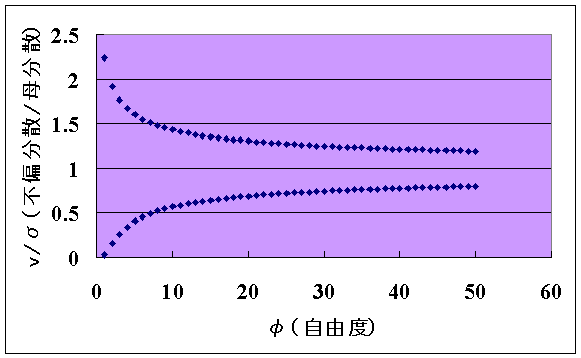
標本分散（s2）および不偏分散（v2）と母分散（σ2）との関係
標本分散（
）および不偏分散（
）と母分散（
）との関係は以下に示すように、自由度
が小さいときはかなり母分散の推定値（
）となる標本分散あるいは不偏分散は母分散からかけ離れた値をとる可能性が高いので、なるべく標本の大きさ
は大きくする必要があります。望ましくは
、少なくとも
であるように標本の大きさを選ぶ必要があります。下表と下図では
あるいは
の比を95%の信頼区間で標示しています。
これらの図表から明らかなように、標本の大きさが
でも
あるいは
は
の食い違いが起こり得ます。その違いを
程度にするには標本の大きさを
程度まで大きくする必要があります。
|
φ=n-1 |
χ2(φ,1-α/2) |
φ=n-1 |
s/σ=√[χ2(φ,1-α/2)/n] |
φ=n-1 |
v/σ=√[χ2(φ,1-α/2)/φ] |
|||||
|
1 |
0.000982 |
|
1 |
0.022159 |
|
|
1 |
0.031338 |
|
|
|
2 |
0.050636 |
|
2 |
0.129918 |
|
|
2 |
0.159116 |
|
|
|
3 |
0.215795 |
|
3 |
0.232269 |
|
|
3 |
0.268201 |
|
|
|
4 |
0.484419 |
|
4 |
0.311262 |
|
|
4 |
0.348001 |
|
|
|
5 |
0.831209 |
|
5 |
0.372203 |
|
|
5 |
0.407728 |
|
|
|
6 |
1.237342 |
|
6 |
0.420432 |
|
|
6 |
0.454119 |
|
|
|
7 |
1.689864 |
|
7 |
0.459601 |
|
|
7 |
0.491334 |
|
|
|
8 |
2.179725 |
|
8 |
0.49213 |
|
|
8 |
0.521982 |
|
|
|
9 |
2.700389 |
|
9 |
0.519653 |
|
|
9 |
0.547762 |
|
|
|
10 |
3.246963 |
|
10 |
0.543303 |
|
|
10 |
0.569821 |
|
|
|
11 |
3.815742 |
|
11 |
0.563896 |
|
|
11 |
0.58897 |
|
|
|
12 |
4.403778 |
|
12 |
0.582024 |
|
|
12 |
0.60579 |
|
|
|
13 |
5.008738 |
|
13 |
0.598136 |
|
|
13 |
0.620715 |
|
|
|
14 |
5.628724 |
|
14 |
0.612575 |
|
|
14 |
0.634075 |
|
|
|
15 |
6.262123 |
|
15 |
0.625606 |
|
|
15 |
0.646123 |
|
|
|
16 |
6.907664 |
|
16 |
0.637443 |
|
|
16 |
0.657061 |
|
|
|
17 |
7.564179 |
|
17 |
0.648253 |
|
|
17 |
0.667047 |
|
|
|
18 |
8.230737 |
|
18 |
0.658177 |
|
|
18 |
0.676212 |
|
|
|
19 |
8.906514 |
|
19 |
0.667327 |
|
|
19 |
0.684663 |
|
|
|
20 |
9.590772 |
|
20 |
0.675798 |
|
|
20 |
0.692487 |
|
|
|
21 |
10.28291 |
|
21 |
0.68367 |
|
|
21 |
0.699759 |
|
|
|
22 |
10.98233 |
|
22 |
0.691008 |
|
|
22 |
0.706539 |
|
|
|
23 |
11.68853 |
|
23 |
0.69787 |
|
|
23 |
0.712879 |
|
|
|
24 |
12.40115 |
|
24 |
0.704305 |
|
|
24 |
0.718828 |
|
|
|
25 |
13.11971 |
|
25 |
0.710355 |
|
|
25 |
0.724423 |
|
|
|
26 |
13.84388 |
|
26 |
0.716056 |
|
|
26 |
0.729696 |
|
|
|
27 |
14.57337 |
|
27 |
0.721441 |
|
|
27 |
0.73468 |
|
|
|
28 |
15.30785 |
|
28 |
0.726538 |
|
|
28 |
0.739398 |
|
|
|
29 |
16.04705 |
|
29 |
0.73137 |
|
|
29 |
0.743873 |
|
|
|
30 |
16.79076 |
|
30 |
0.73596 |
|
|
30 |
0.748126 |
|
|
|
31 |
17.53872 |
|
31 |
0.740328 |
|
|
31 |
0.752174 |
|
|
|
32 |
18.29079 |
|
32 |
0.744491 |
|
|
32 |
0.756034 |
|
|
|
33 |
19.04666 |
|
33 |
0.748462 |
|
|
33 |
0.759718 |
|
|
|
34 |
19.80624 |
|
34 |
0.752258 |
|
|
34 |
0.763241 |
|
|
|
35 |
20.56938 |
|
35 |
0.755891 |
|
|
35 |
0.766614 |
|
|
|
36 |
21.33587 |
|
36 |
0.759372 |
|
|
36 |
0.769846 |
|
|
|
37 |
22.10562 |
|
37 |
0.76271 |
|
|
37 |
0.772948 |
|
|
|
38 |
22.87849 |
|
38 |
0.765916 |
|
|
38 |
0.775929 |
|
|
|
39 |
23.6543 |
|
39 |
0.768998 |
|
|
39 |
0.778794 |
|
|
|
40 |
24.43306 |
|
40 |
0.771964 |
|
|
40 |
0.781554 |
|
|
|
41 |
25.21452 |
|
41 |
0.77482 |
|
|
41 |
0.784212 |
|
|
|
42 |
25.99866 |
|
42 |
0.777573 |
|
|
42 |
0.786775 |
|
|
|
43 |
26.78537 |
|
43 |
0.78023 |
|
|
43 |
0.78925 |
|
|
|
44 |
27.57454 |
|
44 |
0.782795 |
|
|
44 |
0.79164 |
|
|
|
45 |
28.36618 |
|
45 |
0.785274 |
|
|
45 |
0.793952 |
|
|
|
46 |
29.16002 |
|
46 |
0.787671 |
|
|
46 |
0.796187 |
|
|
|
47 |
29.95616 |
|
47 |
0.789992 |
|
|
47 |
0.798351 |
|
|
|
48 |
30.7545 |
|
48 |
0.792239 |
|
|
48 |
0.800449 |
|
|
|
49 |
31.55493 |
|
49 |
0.794417 |
|
|
49 |
0.802483 |
|
|
|
50 |
32.35738 |
|
50 |
0.796529 |
|
|
50 |
0.804455 |
|
|
|
1 |
5.023903 |
|
1 |
1.584914 |
|
|
1 |
2.241406 |
|
|
|
2 |
7.377779 |
|
2 |
1.568203 |
|
|
2 |
1.920648 |
|
|
|
3 |
9.348404 |
|
3 |
1.528758 |
|
|
3 |
1.765258 |
|
|
|
4 |
11.14326 |
|
4 |
1.492867 |
|
|
4 |
1.669076 |
|
|
|
5 |
12.83249 |
|
5 |
1.462446 |
|
|
5 |
1.602029 |
|
|
|
6 |
14.44935 |
|
6 |
1.43673 |
|
|
6 |
1.551846 |
|
|
|
7 |
16.01277 |
|
7 |
1.414778 |
|
|
7 |
1.512461 |
|
|
|
8 |
17.53454 |
|
8 |
1.395809 |
|
|
8 |
1.480479 |
|
|
|
9 |
19.02278 |
|
9 |
1.379231 |
|
|
9 |
1.453837 |
|
|
|
10 |
20.4832 |
|
10 |
1.364591 |
|
|
10 |
1.431195 |
|
|
|
11 |
21.92002 |
|
11 |
1.351543 |
|
|
11 |
1.411641 |
|
|
|
12 |
23.33666 |
|
12 |
1.339824 |
|
|
12 |
1.394533 |
|
|
|
13 |
24.73558 |
|
13 |
1.329221 |
|
|
13 |
1.379397 |
|
|
|
14 |
26.11893 |
|
14 |
1.319569 |
|
|
14 |
1.365884 |
|
|
|
15 |
27.48836 |
|
15 |
1.310734 |
|
|
15 |
1.35372 |
|
|
|
16 |
28.84532 |
|
16 |
1.302607 |
|
|
16 |
1.342696 |
|
|
|
17 |
30.19098 |
|
17 |
1.295097 |
|
|
17 |
1.332644 |
|
|
|
18 |
31.52641 |
|
18 |
1.288132 |
|
|
18 |
1.32343 |
|
|
|
19 |
32.85234 |
|
19 |
1.281646 |
|
|
19 |
1.314941 |
|
|
|
20 |
34.16958 |
|
20 |
1.275587 |
|
|
20 |
1.307088 |
|
|
|
21 |
35.47886 |
|
21 |
1.269912 |
|
|
21 |
1.299796 |
|
|
|
22 |
36.78068 |
|
22 |
1.264579 |
|
|
22 |
1.293 |
|
|
|
23 |
38.07561 |
|
23 |
1.259557 |
|
|
23 |
1.286647 |
|
|
|
24 |
39.36406 |
|
24 |
1.254816 |
|
|
24 |
1.280691 |
|
|
|
25 |
40.6465 |
|
25 |
1.250331 |
|
|
25 |
1.275092 |
|
|
|
26 |
41.92314 |
|
26 |
1.246077 |
|
|
26 |
1.269814 |
|
|
|
27 |
43.19452 |
|
27 |
1.242039 |
|
|
27 |
1.264831 |
|
|
|
28 |
44.46079 |
|
28 |
1.238197 |
|
|
28 |
1.260113 |
|
|
|
29 |
45.72228 |
|
29 |
1.234535 |
|
|
29 |
1.255639 |
|
|
|
30 |
46.97922 |
|
30 |
1.23104 |
|
|
30 |
1.251389 |
|
|
|
31 |
48.23192 |
|
31 |
1.2277 |
|
|
31 |
1.247345 |
|
|
|
32 |
49.48044 |
|
32 |
1.224503 |
|
|
32 |
1.243488 |
|
|
|
33 |
50.7251 |
|
33 |
1.22144 |
|
|
33 |
1.239808 |
|
|
|
34 |
51.96602 |
|
34 |
1.218501 |
|
|
34 |
1.23629 |
|
|
|
35 |
53.20331 |
|
35 |
1.215677 |
|
|
35 |
1.232921 |
|
|
|
36 |
54.43726 |
|
36 |
1.212962 |
|
|
36 |
1.229693 |
|
|
|
37 |
55.66798 |
|
37 |
1.21035 |
|
|
37 |
1.226597 |
|
|
|
38 |
56.89549 |
|
38 |
1.207832 |
|
|
38 |
1.223622 |
|
|
|
39 |
58.12005 |
|
39 |
1.205405 |
|
|
39 |
1.220761 |
|
|
|
40 |
59.34168 |
|
40 |
1.203062 |
|
|
40 |
1.218007 |
|
|
|
41 |
60.56055 |
|
41 |
1.200799 |
|
|
41 |
1.215355 |
|
|
|
42 |
61.77672 |
|
42 |
1.198611 |
|
|
42 |
1.212796 |
|
|
|
43 |
62.99031 |
|
43 |
1.196494 |
|
|
43 |
1.210327 |
|
|
|
44 |
64.20141 |
|
44 |
1.194445 |
|
|
44 |
1.207942 |
|
|
|
45 |
65.41013 |
|
45 |
1.192459 |
|
|
45 |
1.205636 |
|
|
|
46 |
66.61647 |
|
46 |
1.190534 |
|
|
46 |
1.203405 |
|
|
|
47 |
67.82064 |
|
47 |
1.188667 |
|
|
47 |
1.201246 |
|
|
|
48 |
69.02257 |
|
48 |
1.186855 |
|
|
48 |
1.199154 |
|
|
|
49 |
70.22236 |
|
49 |
1.185094 |
|
|
49 |
1.197125 |
|
|
|
50 |
71.42019 |
|
50 |
1.183383 |
|
|
50 |
1.195159 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
74.22188 |
|
100 |
0.857246 |
|
|
100 |
0.861521 |
|
|
|
100 |
129.5613 |
|
100 |
1.132601 |
|
|
100 |
1.13825 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
914.2572 |
|
1000 |
0.95569 |
|
|
1000 |
0.956168 |
|
|
|
1000 |
1089.531 |
|
1000 |
1.043284 |
|
|
1000 |
1.043806 |
|
|
