不確かさの伝播則による合成標準不確かさの求め方
ある実験系での測定の目的とは「測定量」(measurand)![]() の値すなわち観測される特定の量(particular
quantity)の値を決定することです。したがって、測定にあたっては、測定量の評価に対して適切な「測定の方法」(method of measurement)および「測定の手順」(measurement procedure)をまず最初に明示しておかなければならず、また、「測定の結果」(result of a measurement)
の値すなわち観測される特定の量(particular
quantity)の値を決定することです。したがって、測定にあたっては、測定量の評価に対して適切な「測定の方法」(method of measurement)および「測定の手順」(measurement procedure)をまず最初に明示しておかなければならず、また、「測定の結果」(result of a measurement)![]() は一般に「測定量の値」の近似値あるいは「推定値」(estimate)に過ぎないことから、その推定値の「不確かさ」(uncertainty)も併せて明記しなければならないと、GUMは謳っています。
は一般に「測定量の値」の近似値あるいは「推定値」(estimate)に過ぎないことから、その推定値の「不確かさ」(uncertainty)も併せて明記しなければならないと、GUMは謳っています。
多くの場合、「測定量」(物理量)![]() は、直接には測定されず、他の
は、直接には測定されず、他の![]() 個の量
個の量![]() から
から
![]()
のような関数関係![]() によって決定されます。
によって決定されます。
「測定量![]() の推定値」(an
estimate of the measurand
の推定値」(an
estimate of the measurand ![]() )、すなわち、「出力推定値」(output
estimate)
)、すなわち、「出力推定値」(output
estimate)![]() は、
は、![]() 個の量
個の量![]() に対する「入力推定値」(input
estimate)
に対する「入力推定値」(input
estimate)![]() を用いて
を用いて
![]()
![]()
のように表すことができます。
「出力推定値」あるいは「測定結果」![]() に付随する推定標準偏差
に付随する推定標準偏差![]() を「合成標準不確かさ」(combined
standard uncertainty)と呼び、記号
を「合成標準不確かさ」(combined
standard uncertainty)と呼び、記号![]() で表します。また、これは、「標準不確かさ」と呼ばれ
で表します。また、これは、「標準不確かさ」と呼ばれ![]() で表される、それぞれの「入力推定値」
で表される、それぞれの「入力推定値」![]() の推定標準偏差
の推定標準偏差![]() を合成することにより求めることができます。
を合成することにより求めることができます。
入力量![]() がすべて「独立」な場合は、測定量
がすべて「独立」な場合は、測定量![]() の推定値、すなわち、測定の結果
の推定値、すなわち、測定の結果![]() の合成標準不確かさ
の合成標準不確かさ![]() は、次式で与えられる合成分散(combined
variance)
は、次式で与えられる合成分散(combined
variance)![]() の正の平方根となります。
の正の平方根となります。
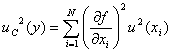
ここで、![]() は上述の関数
は上述の関数![]() を表す写像記号であり、
を表す写像記号であり、![]() は「感度係数」(sensitivity
coefficient)と呼ばれています。感度係数は実験的に求められる場合もあり理論的・経験的に求められる場合もあります。このようにして求められた合成標準不確かさ
は「感度係数」(sensitivity
coefficient)と呼ばれています。感度係数は実験的に求められる場合もあり理論的・経験的に求められる場合もあります。このようにして求められた合成標準不確かさ![]() は推定標準偏差
は推定標準偏差![]() であり、「合理的に測定量(物理量)
であり、「合理的に測定量(物理量)![]() に結びつけられ得る値の分散」を特徴づけるものです。また、この式は「不確かさの伝播則」(the law of propagation of uncertainty)という重要な公式です。
に結びつけられ得る値の分散」を特徴づけるものです。また、この式は「不確かさの伝播則」(the law of propagation of uncertainty)という重要な公式です。
「不確かさの伝播則」の基となる関数
![]()
が、もし次式のような指数関数
![]()
であった場合には、合成標準不確かさ![]() を上述の「不確かさの伝播則」の公式をそのまま使って計算するよりも、この関数の対数をとり
を上述の「不確かさの伝播則」の公式をそのまま使って計算するよりも、この関数の対数をとり
![]()
を微分して計算した方が簡単です。すなわち
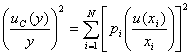
の式から合成標準不確かさ![]() を算出することができます。合成分散
を算出することができます。合成分散![]() は「相対合成分散」
は「相対合成分散」![]() として、各入力値の推定分散
として、各入力値の推定分散![]() は「相対推定分散」
は「相対推定分散」![]() として表せます。また、「相対合成標準不確かさ」は
として表せます。また、「相対合成標準不確かさ」は![]() であり、各入力推定値の「相対標準不確かさ」は
であり、各入力推定値の「相対標準不確かさ」は![]() です。ただし、
です。ただし、![]() および
および![]() とします。
とします。
(例題)いま![]() の金の容器に入れた
の金の容器に入れた![]() のダイヤモンドを
のダイヤモンドを![]() ℃から
℃から![]() ℃まで
℃まで![]() だけ温めるのに必要な熱量
だけ温めるのに必要な熱量![]() を求め、その測定量
を求め、その測定量![]() に不確かさを併記することを考えましょう。ただし、金の密度は
に不確かさを併記することを考えましょう。ただし、金の密度は![]() であり、ダイヤモンドの密度は
であり、ダイヤモンドの密度は![]() とし、それぞれの定圧比熱は
とし、それぞれの定圧比熱は![]() および
および![]() とします。また、各入力量の推定標準偏差は、それぞれ、
とします。また、各入力量の推定標準偏差は、それぞれ、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() であり、温度上昇の推定標準偏差は
であり、温度上昇の推定標準偏差は![]() とします。
とします。

(解答)求める熱量![]() を表す関数式は
を表す関数式は
![]()
ですから、求める熱量![]() の推定値
の推定値![]() は
は
![]()
となります。また、不確かさの伝播則より、求める合成分散![]() は
は
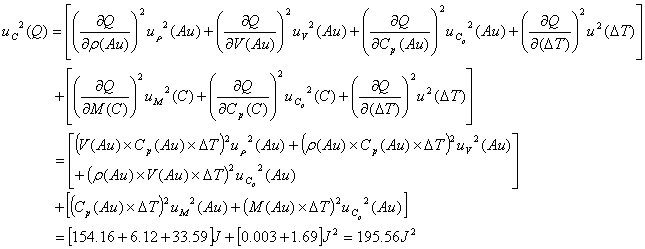
となるので、合成標準不確かさ![]() は
は
![]()
となります。したがって、包含係数![]() とすれば拡張不確かさ
とすれば拡張不確かさ![]() は
は
![]()
となるので、信頼の水準が約![]() の熱量
の熱量![]() の信頼区間は
の信頼区間は
![]()
となります。