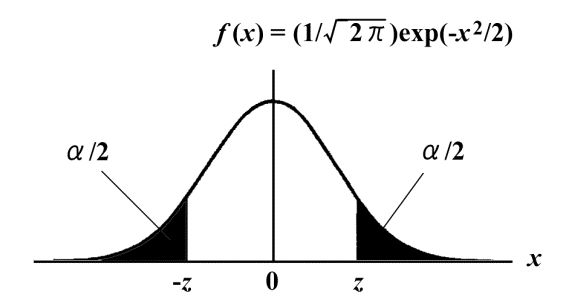
標準正規分布表

 

　下表は標準正規分布の確率密度関数

 

               

 

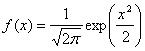
において確率変数の値をからまで積分した陰影部の面積

 

               

 

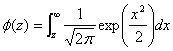
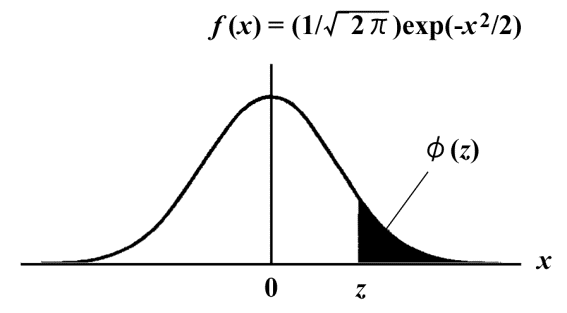
の値を確率変数に対して記載したものです。この確率の値はMicrosoftのExcel表計算ソフトのメニュバーにある「関数の貼り付け」（）で「関数の分類」で統計を選び「関数名」でNORMSDISTを選んだ後、その入力欄でZに所望する値（z）を入れて、得られる値を1から引けば得られます。すなわち1−NORMSDIST(z)が表の値となります。

 

 

正規分布

z

0

1

2

3

4

5

6

7

8

9

 

0

0.5

0.496011

0.492022

0.488033

0.484047

0.480061

0.476078

0.472097

0.468119

0.464144

 

0.1

0.460172

0.456205

0.452242

0.448283

0.44433

0.440382

0.436441

0.432505

0.428576

0.424655

 

0.2

0.42074

0.416834

0.412936

0.409046

0.405165

0.401294

0.397432

0.39358

0.389739

0.385908

 

0.3

0.382089

0.378281

0.374484

0.3707

0.366928

0.363169

0.359424

0.355691

0.351973

0.348268

 

0.4

0.344578

0.340903

0.337243

0.333598

0.329969

0.326355

0.322758

0.319178

0.315614

0.312067

 

0.5

0.308538

0.305026

0.301532

0.298056

0.294598

0.29116

0.28774

0.284339

0.280957

0.277595

 

0.6

0.274253

0.270931

0.267629

0.264347

0.261086

0.257846

0.254627

0.251429

0.248252

0.245097

 

0.7

0.241964

0.238852

0.235762

0.232695

0.22965

0.226627

0.223627

0.22065

0.217695

0.214764

 

0.8

0.211855

0.20897

0.206108

0.203269

0.200454

0.197662

0.194894

0.19215

0.18943

0.186733

 

0.9

0.18406

0.181411

0.178786

0.176186

0.173609

0.171056

0.168528

0.166023

0.163543

0.161087

σ

1

0.158655

0.156248

0.153864

0.151505

0.14917

0.146859

0.144572

0.14231

0.140071

0.137857

 

1.1

0.135666

0.1335

0.131357

0.129238

0.127143

0.125072

0.123024

0.121001

0.119

0.117023

 

1.2

0.11507

0.11314

0.111233

0.109349

0.107488

0.10565

0.103835

0.102042

0.100273

0.098525

 

1.3

0.096801

0.095098

0.093418

0.091759

0.090123

0.088508

0.086915

0.085344

0.083793

0.082264

 

1.4

0.080757

0.07927

0.077804

0.076359

0.074934

0.073529

0.072145

0.070781

0.069437

0.068112

 

1.5

0.066807

0.065522

0.064256

0.063008

0.06178

0.060571

0.05938

0.058208

0.057053

0.055917

 

1.6

0.054799

0.053699

0.052616

0.051551

0.050503

0.049471

0.048457

0.04746

0.046479

0.045514

 

1.7

0.044565

0.043633

0.042716

0.041815

0.040929

0.040059

0.039204

0.038364

0.037538

0.036727

 

1.8

0.03593

0.035148

0.034379

0.033625

0.032884

0.032157

0.031443

0.030742

0.030054

0.029379

 

1.9

0.028716

0.028067

0.027429

0.026803

0.02619

0.025588

0.024998

0.024419

0.023852

0.023295

2σ

2

0.02275

0.022216

0.021692

0.021178

0.020675

0.020182

0.019699

0.019226

0.018763

0.018309

 

2.1

0.017864

0.017429

0.017003

0.016586

0.016177

0.015778

0.015386

0.015003

0.014629

0.014262

 

2.2

0.013903

0.013553

0.013209

0.012874

0.012545

0.012224

0.011911

0.011604

0.011304

0.011011

 

2.3

0.010724

0.010444

0.01017

0.009903

0.009642

0.009387

0.009137

0.008894

0.008656

0.008424

 

2.4

0.008198

0.007976

0.00776

0.007549

0.007344

0.007143

0.006947

0.006756

0.006569

0.006387

 

2.5

0.00621

0.006037

0.005868

0.005703

0.005543

0.005386

0.005234

0.005085

0.00494

0.004799

 

2.6

0.004661

0.004527

0.004397

0.004269

0.004145

0.004025

0.003907

0.003793

0.003681

0.003573

 

2.7

0.003467

0.003364

0.003264

0.003167

0.003072

0.00298

0.00289

0.002803

0.002718

0.002635

 

2.8

0.002555

0.002477

0.002401

0.002327

0.002256

0.002186

0.002118

0.002052

0.001988

0.001926

 

2.9

0.001866

0.001807

0.00175

0.001695

0.001641

0.001589

0.001538

0.001489

0.001441

0.001395

3σ

3

0.00135

0.001306

0.001264

0.001223

0.001183

0.001144

0.001107

0.00107

0.001035

0.001001

 

3.1

0.000968

0.000936

0.000904

0.000874

0.000845

0.000816

0.000789

0.000762

0.000736

0.000711

 

3.2

0.000687

0.000664

0.000641

0.000619

0.000598

0.000577

0.000557

0.000538

0.000519

0.000501

 

3.3

0.000483

0.000467

0.00045

0.000434

0.000419

0.000404

0.00039

0.000376

0.000362

0.00035

 

3.4

0.000337

0.000325

0.000313

0.000302

0.000291

0.00028

0.00027

0.00026

0.000251

0.000242

 

3.5

0.000233

0.000224

0.000216

0.000208

0.0002

0.000193

0.000185

0.000179

0.000172

0.000165

 

3.6

0.000159

0.000153

0.000147

0.000142

0.000136

0.000131

0.000126

0.000121

0.000117

0.000112

 

3.7

0.000108

0.000104

9.96E-05

9.58E-05

9.2E-05

8.84E-05

8.5E-05

8.16E-05

7.84E-05

7.53E-05

 

3.8

7.24E-05

6.95E-05

6.67E-05

6.41E-05

6.15E-05

5.91E-05

5.67E-05

5.44E-05

5.22E-05

5.01E-05

 

3.9

4.81E-05

4.62E-05

4.43E-05

4.25E-05

4.08E-05

3.91E-05

3.75E-05

3.6E-05

3.45E-05

3.31E-05

4σ

4

3.17E-05

3.04E-05

2.91E-05

2.79E-05

2.67E-05

2.56E-05

2.45E-05

2.35E-05

2.25E-05

2.16E-05

 

4.1

2.07E-05

1.98E-05

1.9E-05

1.81E-05

1.74E-05

1.66E-05

1.59E-05

1.52E-05

1.46E-05

1.4E-05

 

4.2

1.34E-05

1.28E-05

1.22E-05

1.17E-05

1.12E-05

1.07E-05

1.02E-05

9.78E-06

9.35E-06

8.94E-06

 

4.3

8.55E-06

8.17E-06

7.81E-06

7.46E-06

7.13E-06

6.81E-06

6.51E-06

6.22E-06

5.94E-06

5.67E-06

 

4.4

5.42E-06

5.17E-06

4.94E-06

4.72E-06

4.5E-06

4.3E-06

4.1E-06

3.91E-06

3.74E-06

3.56E-06

 

4.5

3.4E-06

3.24E-06

3.09E-06

2.95E-06

2.82E-06

2.68E-06

2.56E-06

2.44E-06

2.33E-06

2.22E-06

 

4.6

2.11E-06

2.02E-06

1.92E-06

1.83E-06

1.74E-06

1.66E-06

1.58E-06

1.51E-06

1.44E-06

1.37E-06

 

4.7

1.3E-06

1.24E-06

1.18E-06

1.12E-06

1.07E-06

1.02E-06

9.69E-07

9.22E-07

8.78E-07

8.35E-07

 

4.8

7.94E-07

7.56E-07

7.19E-07

6.84E-07

6.5E-07

6.18E-07

5.88E-07

5.59E-07

5.31E-07

5.05E-07

 

4.9

4.8E-07

4.56E-07

4.33E-07

4.12E-07

3.91E-07

3.72E-07

3.53E-07

3.35E-07

3.18E-07

3.02E-07

5σ

5

2.87E-07

2.73E-07

2.59E-07

2.46E-07

2.33E-07

2.21E-07

2.1E-07

1.99E-07

1.89E-07

1.79E-07

 

　上の表の値は、下図のように、標準正規分布の信頼水準での両側検定における陰影部分の面積（危険率）のちょうど半分の面積に相当する確率と等しくなっています。