正規分布
測定誤差のバラツキや社会現象あるいは自然現象の中に現れるバラツキの多くは釣鐘型をした正規分布であることから、この分布は統計学の中でも最も重要で応用性の広い分布です。母集団が正規分布に従っているとき、これを正規母集団と呼び、その母平均を![]() 、母分散を
、母分散を![]() (母標準偏差はしたがって
(母標準偏差はしたがって![]() )としたとき、一般に
)としたとき、一般に![]() なる記号で表します。正規分布の形状は、下図のように、母平均
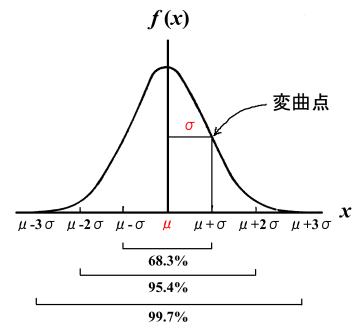
なる記号で表します。正規分布の形状は、下図のように、母平均![]() を中心として左右対称になった釣鐘型形状をしており、その関数
を中心として左右対称になった釣鐘型形状をしており、その関数![]() の変曲点までの距離がちょうど母標準偏差
の変曲点までの距離がちょうど母標準偏差![]() となっています。確率変数
となっています。確率変数![]() の実現値である変数
の実現値である変数![]() の出現確率
の出現確率![]() を示す式を確率密度関数と呼び、それを
を示す式を確率密度関数と呼び、それを![]() としますと、正規分布の確率密度関数
としますと、正規分布の確率密度関数![]() は
は

となります。
このように関数![]() は確率変数
は確率変数![]() の他には母平均
の他には母平均![]() と母分散
と母分散![]() しか含まず、またこの母平均と母分散がその関数
しか含まず、またこの母平均と母分散がその関数![]() の形状を特徴づけていることから、正規母集団の母数として母平均
の形状を特徴づけていることから、正規母集団の母数として母平均![]() と母分散
と母分散![]() が選ばれます。関数
が選ばれます。関数![]() を確率変数
を確率変数![]() の全領域で積分した値は確率100%すなわち1となります。
の全領域で積分した値は確率100%すなわち1となります。
![]()
また、この確率変数![]() の期待値
の期待値![]() と分散
と分散![]() は
は
![]()
となります。
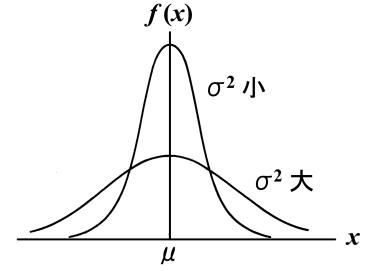
「塵(ちり)も積もれば山となる」という諺がありますが、正にちりのような小さな誤差の集積が正規分布(上図参照)のような山を作り出しているので、正規分布のことを「誤差分布」ということもあります。このちりの積もり方(分散![]() に相当)によって山の形が変わってきます。
に相当)によって山の形が変わってきます。
ところで、確率変数![]() と平均
と平均![]() との差の
との差の![]() 乗の期待値を
乗の期待値を![]() 次のモーメントと呼び、
次のモーメントと呼び、![]() で表すと
で表すと
![]()
となります。![]() の場合は
の場合は![]() となり、2次のモーメント
となり、2次のモーメント![]() は正規分布の分散
は正規分布の分散![]() に相当します。また、モーメントの定義式から明らかなように、分布の形状が平均
に相当します。また、モーメントの定義式から明らかなように、分布の形状が平均![]() を中心として、正規分布のように、左右対称になっていれば奇数次のモーメントはいつも
を中心として、正規分布のように、左右対称になっていれば奇数次のモーメントはいつも![]() になります。また、3次のモーメント
になります。また、3次のモーメント
![]()
を標準偏差![]() の3乗
の3乗![]() で割ったものは
で割ったものは
![]()
と呼ばれ、分布の非対称性の度合いとしてよく用いられます。正規分布は母分散![]() を中心として左右対称の形状をした密度関数であることから歪度は0となります。正規分布では、奇数次のモーメントは0であり、偶数次のモーメントは一般式
を中心として左右対称の形状をした密度関数であることから歪度は0となります。正規分布では、奇数次のモーメントは0であり、偶数次のモーメントは一般式
![]()
で表すことができます。一般に、4次のモーメントと2次のモーメントの2乗の比![]() のことを
のことを
![]()
と呼んでいますが、正規分布の場合は上述の偶数次のモーメントの一般式より
![]()
となります。したがって、正規分布の尖度は
![]()
になるので、ある分布が与えられたとき歪度が0で尖度が3にどれだけ近いかを判定すれば、その分布が正規分布かどうかを判断することができます。
正規分布には次のような重要な性質があります。![]()
(1) 正規母集団![]() から無作為意抽出した大きさ
から無作為意抽出した大きさ![]() の標本の平均
の標本の平均![]() は、下図のように、平均が
は、下図のように、平均が![]() で分散が
で分散が![]() の正規分布
の正規分布![]() になります。
になります。


(2)2つの互いに独立な確率変数![]() がつくる2つの正規分布
がつくる2つの正規分布![]() と
と![]() の和は、確率変数の和
の和は、確率変数の和![]() がつくる分布であり、これは、下図のように、平均が
がつくる分布であり、これは、下図のように、平均が![]() で分散が
で分散が![]() の正規分布
の正規分布![]() になります。正規分布の和は正規分布の単なる重ね合わせではないことに注意しなければなりません。
になります。正規分布の和は正規分布の単なる重ね合わせではないことに注意しなければなりません。

正規分布![]() の確率密度関数
の確率密度関数![]() は
は
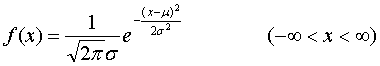
ですが、確率変数![]() を
を
![]()
のように、新たな確率変数![]() に変更することを「標準化」と呼んでいます。そして、この新しい標準化変数
に変更することを「標準化」と呼んでいます。そして、この新しい標準化変数![]() を使って書き直した正規分布の確率密度関数
を使って書き直した正規分布の確率密度関数![]()
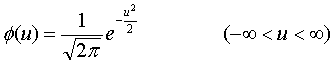
で表現される分布のことを特に「標準正規分布」あるいは「基準正規分布」(standard normal distribution)と呼び、![]() あるいは単に
あるいは単に![]() という記号で書き表します。標準正規分布は記述統計学のみならず推測統計学においてもきわめて重要な統計分布です。
という記号で書き表します。標準正規分布は記述統計学のみならず推測統計学においてもきわめて重要な統計分布です。