母数と統計量
確率母分布(random population distribution)の「原点の回りの1次モーメント」(1st raw moment)が母平均(![]() )を、「母平均の回りの2次モーメント」(2nd raw moment)が母分散(
)を、「母平均の回りの2次モーメント」(2nd raw moment)が母分散(![]() )を表すように、一般に「母分布のモーメント(積率)」は母集団の特性を表す統計値(母集団特性値)であり、これをとくに「母数」(population parameter)と呼んでいます。
)を表すように、一般に「母分布のモーメント(積率)」は母集団の特性を表す統計値(母集団特性値)であり、これをとくに「母数」(population parameter)と呼んでいます。
これと同様に、「標本の度数分布(sample frequency distribution)のモーメント」は標本集団の特性を表す特性値(標本集団特性値)であり、これを標本統計量(sample statistic)あるいは単に「統計量」(statistic)と呼んでいます。
母数と統計量が違う点は、前者が母集団に固有の定数であるのに対して、後者は標本集団が異なるごとに異なる確率定数であることです。統計量の代表的なものとしては標本平均(![]() )や標本分散(
)や標本分散(![]() )や不偏分散(
)や不偏分散(![]() )などがあります。
)などがあります。
母集団の各変数![]() (観測値)の個数は
(観測値)の個数は![]() であると上では定義しましたが、最近の推測統計学では
であると上では定義しましたが、最近の推測統計学では![]() である無限母集団の母数(母平均
である無限母集団の母数(母平均![]() と母分散
と母分散![]() )をそれから無作為抽出(random
sampling)した標本集団の統計量(標本平均
)をそれから無作為抽出(random
sampling)した標本集団の統計量(標本平均![]() と不偏分散
と不偏分散![]() )から推定する場合が一般的です。母集団から無作為抽出した標本の各変数の分布は母集団の分布と限りなく近いものになるはずですが、標本数(
)から推定する場合が一般的です。母集団から無作為抽出した標本の各変数の分布は母集団の分布と限りなく近いものになるはずですが、標本数(![]() )が少なければ少ないほど標本分布は母集団分布とはかけ離れたものになるであろうことは容易に想像がつきます。また、標本数が同じであっても母集団の変数からどれとどれが選ばれるかによって標本ごとに違った分布となり、それらの標本分布から算出される標本平均
)が少なければ少ないほど標本分布は母集団分布とはかけ離れたものになるであろうことは容易に想像がつきます。また、標本数が同じであっても母集団の変数からどれとどれが選ばれるかによって標本ごとに違った分布となり、それらの標本分布から算出される標本平均![]() と不偏分散
と不偏分散![]() の値も標本ごとに変わり得ることは自明でしょう。すなわち、母集団の母数(母平均
の値も標本ごとに変わり得ることは自明でしょう。すなわち、母集団の母数(母平均![]() と母分散
と母分散![]() )を推定するはずの標本の統計量(標本平均
)を推定するはずの標本の統計量(標本平均![]() と不偏分散
と不偏分散![]() )は、標本の選び方により値は異なるが、標本の選び方が母集団からの完全な無作為抽出である限り、標本分布もそれから得られる統計量も完全に確率的なものになると考えられます。したがって、標本の変数は確率変数と呼ばれ、標本の
)は、標本の選び方により値は異なるが、標本の選び方が母集団からの完全な無作為抽出である限り、標本分布もそれから得られる統計量も完全に確率的なものになると考えられます。したがって、標本の変数は確率変数と呼ばれ、標本の![]() 番目の変数
番目の変数![]() は確率変数であることを明示するために英大文字の
は確率変数であることを明示するために英大文字の![]() で表されるのが一般的です。したがって、この確率変数
で表されるのが一般的です。したがって、この確率変数![]() の実現値が標本の
の実現値が標本の![]() 番目の変数
番目の変数![]() に相当することになります。
に相当することになります。
(注)モーメント(moment)とは?
標本分布(sample distribution)の代表値から標本平均を引いた偏差のベキ乗和を総度数で平均したものは標本分布の特性をよく表すことが知られています。たとえば、各変数の算術平均(標本平均)からの偏差の2乗和を総度数で割ったものが統計学で言う「分散」であり、偏差の3乗和を総度数で割ったものが「歪度」、偏差の4乗和を総度数で割ったものが「尖度」に相当します。
統計学では、このように各変数![]() の算術平均(標本平均)
の算術平均(標本平均)![]() からの偏差
からの偏差![]() のr乗の総和
のr乗の総和![]() を総度数
を総度数![]() で平均化したもの、すなわち
で平均化したもの、すなわち
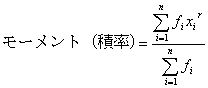
あるいは、もっと詳しくは、「算術平均まわりのr次モーメント」と呼んでいます。ここで、![]()
![]() は度数(frequency)で変数
は度数(frequency)で変数![]() の事象が起こる度合いを表しています。統計学で言う「モーメント」は力学で言う「力のモーメント」に相当し、上述の変数
の事象が起こる度合いを表しています。統計学で言う「モーメント」は力学で言う「力のモーメント」に相当し、上述の変数![]() は力学のてこの原理における支点からの距離、度数
は力学のてこの原理における支点からの距離、度数![]() はそこにかかる力の大きさに相当します。
はそこにかかる力の大きさに相当します。
そこで、原点を支点にした「原点まわりのr次モーメント」と算術平均を支点にした「算術平均まわりのr次モーメント」をそれぞれνrおよびμrとすれば

と定義することができます。ちなみに、![]() であるから、
であるから、![]() です。
です。
これらの定義式を使って標本の統計量を表せば次のようになります。
標本平均(算術平均): ![]()
標本分散: ![]()
標準偏差: ![]()

ここで、統計学で最も重要な概念である「平均」と「分散」についてもう少し考えてみましょう。いま、確率変数![]() の実現値
の実現値![]() である事象が下図のような度数分布をしているものとすると、それらの変数
である事象が下図のような度数分布をしているものとすると、それらの変数![]() の平均
の平均![]() は
は
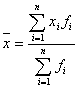
です。ここで、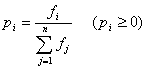 なる変換を行えば
なる変換を行えば![]() は
は![]() という事象が起きる確率であり、
という事象が起きる確率であり、![]() だから、全体集合(あるいは標本空間とも言う)
だから、全体集合(あるいは標本空間とも言う)![]() がつくる度数分布は確率分布であるとも言えます。そうすると、この全事象の平均
がつくる度数分布は確率分布であるとも言えます。そうすると、この全事象の平均![]() は
は
![]()
と書くことができます。

上述の確率分布は![]() は離散的な集合であったが、これを連続的な確率分布に発展させるために、離散的な確率
は離散的な集合であったが、これを連続的な確率分布に発展させるために、離散的な確率![]() を連続的な確率密度
を連続的な確率密度![]() に置き換えると、その連続的な集合
に置き換えると、その連続的な集合![]() の平均
の平均![]() は
は
![]()
と定義されます。ただし、確率密度![]() は
は
![]()
です。すなわち、平均![]() は確率密度分布
は確率密度分布![]() の平均に相当します。
の平均に相当します。
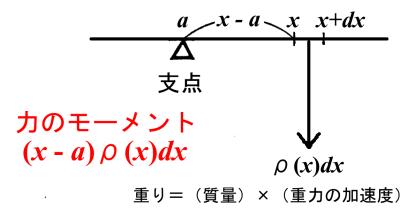
いま、![]() を質量密度と仮定すると、下図のように、
を質量密度と仮定すると、下図のように、![]() の部分の重さは
の部分の重さは![]() であり、支点
であり、支点![]() の周りの力のモーメント(トルクとも言う)
の周りの力のモーメント(トルクとも言う)![]() は
は
![]()
となります。重心はこの力のモーメント![]() の総和が0になるところ、すなわち
の総和が0になるところ、すなわち
![]()
の式を満足する![]() の位置になります。
の位置になります。
したがって、上式を変形すれば
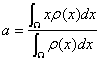
となるが、分子は定義より標本空間![]() の平均
の平均![]() であり、分母は確率密度
であり、分母は確率密度![]() の定義より1であるので、
の定義より1であるので、
![]()
となります。すなわち、標本空間![]() の平均
の平均![]() は剛体の重心に相当します。
は剛体の重心に相当します。
一方、次式
![]()
で定義される![]() は「
は「![]() の周りの分散」と言い、とくに平均
の周りの分散」と言い、とくに平均![]() の周りの分散のことを単に「分散」と呼び、一般に
の周りの分散のことを単に「分散」と呼び、一般に![]() の記号で表します。また、
の記号で表します。また、![]() は「標準偏差」と呼ばれ、標準不確かさ
は「標準偏差」と呼ばれ、標準不確かさ![]() に相当する重要なものです。
に相当する重要なものです。
確率密度分布![]() の平均および分散を統計学では確率変数
の平均および分散を統計学では確率変数![]() の平均や分散と言います。ところで、
の平均や分散と言います。ところで、
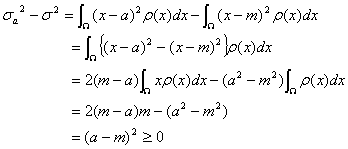
であるから、下図のように、平均![]() とは分散が最小になる特殊な点であることがわかります。分散とは重心
とは分散が最小になる特殊な点であることがわかります。分散とは重心![]() の周りの慣性モーメント
の周りの慣性モーメント![]() であり、その剛体の慣性モーメント
であり、その剛体の慣性モーメント![]() が最小となる位置(
が最小となる位置(![]() )が平均
)が平均![]() であると言うこともできます。すなわち、
であると言うこともできます。すなわち、
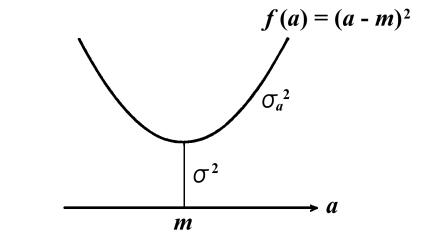
平均![]() とは、標本空間
とは、標本空間![]() (全事象)の
(全事象)の![]() -加法族
-加法族![]() の上の最も安定な点(剛体で言えば重心の位置)であると言えます。
の上の最も安定な点(剛体で言えば重心の位置)であると言えます。
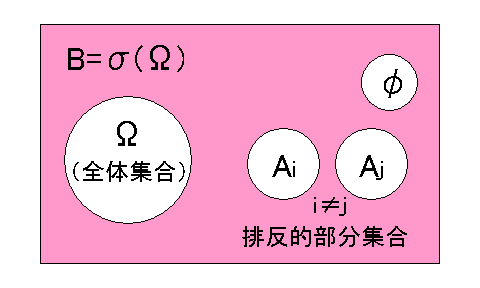
(参考)集合論から眺めた確率空間
空でない集合![]() 上の加算加法族(
上の加算加法族(![]() -加法族とも言う)
-加法族とも言う)![]() で定義された実数値関数
で定義された実数値関数![]() (1次元ユークリッド空間)が次のような3条件を満たすとき、
(1次元ユークリッド空間)が次のような3条件を満たすとき、![]() の組
の組![]() を確率空間、
を確率空間、![]() を標本空間、
を標本空間、![]() の元を(確率)事象、関数値
の元を(確率)事象、関数値![]() を事象
を事象![]() の起こる確率と言います。ここで、
の起こる確率と言います。ここで、![]() は全事象
は全事象![]() の部分集合の全体である
の部分集合の全体である![]() -加法族
-加法族![]() です。また、標本空間
です。また、標本空間![]() が
が![]() 次元ユークリッド空間
次元ユークリッド空間![]() であるならば、
であるならば、![]() の任意の閉集合全体を含む最小の
の任意の閉集合全体を含む最小の![]() -加法族を考えたとき、これをボレル(Borel)集合族と呼んでいます。
-加法族を考えたとき、これをボレル(Borel)集合族と呼んでいます。
(1)![]()
(2)![]()
(3)![]()
ここで、![]() は合併集合あるいは和集合(union)と呼ばれる記号で
は合併集合あるいは和集合(union)と呼ばれる記号で
![]()
と等価であり、事象![]() がいずれも起こり得ることを表しています。
がいずれも起こり得ることを表しています。
また、「事象」(event)とは空間におけるある行為すなわち「試行」(trial)の結果起こった事柄であり、それ以上に分けられない事象を根元事象(elementary
event)と言い、根元事象全体の集まりを集合(set)と呼び通常![]() という記号で表します。そして、集合を形成している個々の事象をその集合の要素あるいは元(element)と言います。要素のない集合は空集合(null set)と呼ばれ
という記号で表します。そして、集合を形成している個々の事象をその集合の要素あるいは元(element)と言います。要素のない集合は空集合(null set)と呼ばれ![]() という記号で表されます。これに対し集合
という記号で表されます。これに対し集合![]() は全体集合(universe)と呼ばれます。
は全体集合(universe)と呼ばれます。
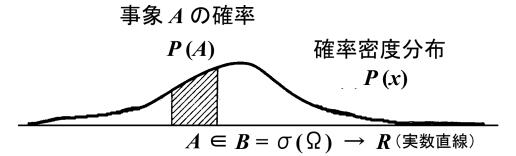
いま、全体集合(事象の全体)![]() の要素の数を
の要素の数を![]() と書き、また
と書き、また![]() の部分集合(subset)
の部分集合(subset)![]() の要素の数を
の要素の数を![]() で表すことにします。このとき、どの根元事象も同程度の確かさで起こるとすれば、事象
で表すことにします。このとき、どの根元事象も同程度の確かさで起こるとすれば、事象![]() の確率(数学的確率)
の確率(数学的確率)![]() は
は
![]()
と定義することができます。![]() は負にはならず
は負にはならず![]() を超えることはないので
を超えることはないので
![]()
という関係が成立します。部分集合![]() は全体集合
は全体集合![]() の部分集合の全体である集合
の部分集合の全体である集合![]() (
(![]() 上の可算加法族(
上の可算加法族(![]() -加法族
-加法族![]() )である)の中に含まれるので
)である)の中に含まれるので
![]()
という関係も成立します。
部分集合![]() の中にある根元事象を
の中にある根元事象を![]() とすれば、各根元事象は互いに排反的(exclusive)、すなわち
とすれば、各根元事象は互いに排反的(exclusive)、すなわち
![]()
のように共通部分(intersection)がないから、確率の加法定理
![]()
より
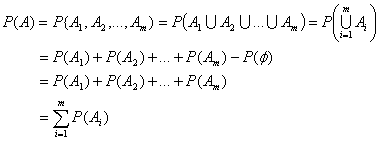
という関係式が導かれます。そして、このような関係が成り立つ全体集合![]() (標本空間)とボレル集合族
(標本空間)とボレル集合族![]() および確率
および確率![]() が作る組
が作る組![]() のことを「確率空間」と呼んでいます。
のことを「確率空間」と呼んでいます。