分散分析法と構造モデル

データの構造

　ある触媒を使った化学反応（A+B→C）において反応温度を変えた実験を行い、反応収率（%）を各温度条件毎に4回繰り返し測定をしたら、下表のような結果が得られました。ただし、反応温度の選び方は40℃、60℃、80℃と固定ですが、3×4=12回の実験そのものは順序は完全にランダムに行ったものとします。また、この実験結果は横軸を反応温度、縦軸を反応収率とすれば下図のようになります。

	反応温度（因子A）
実験の繰り返し番号	A1=40℃	A2=60℃	A3=80℃
1	63.2	70.3	80.2
2	64.0	71.0	83.3
3	62.8	69.6	82.0
4	63.5	71.2	81.4

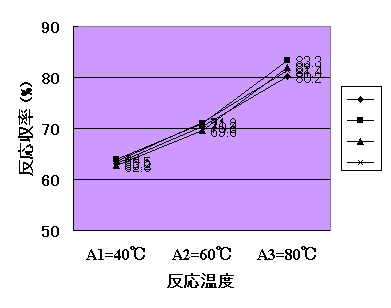
　上図から明らかなように、実験の繰り返しによるデータのバラツキは小さく（繰り返し実験は完全にランダムに行われているから、それに基づく変動誤差は偶然誤差）であるから、それに比べ反応温度が変動するとデータのバラツキは大きくなり、結果として反応温度が反応収率に一定の説明可能な影響を与えている（反応温度が上がれば反応収率が上がる）ことがわかります。

この例のように、実験データに大きな影響を与え得る可能性のある主要な変動要因（これを因子Aとします）が１つで、残りの変動要因がランダムな実験の繰り返しすなわち偶然誤差であるような場合の統計モデルを「１因子実験」あるいは「１元配置実験」と呼んでいます。また、この場合、因子Aである反応温度は３種類選びましたが、この３種類それぞれの実験条件のことを因子Aの水準と呼び、その種類の数のことを水準数と呼んでいます。上例では因子Aは反応温度であり、その水準は40℃、60℃、80℃の３種類であり、したがって水準数となります。偶然誤差の基となるランダムな繰り返し実験の繰返し数はこの場合となっています。

　ところで、この１元配置実験においては、母集団としての無限にあり得る反応温度の条件から、サンプルとして特に40℃、60℃、80℃の３種類の因子を選んだのであるが、一般的にこのような場合にはある反応温度で反応収率がどのように変わるのかということに関心があるのが普通であり、そのような因子のことを「母数型」因子と呼んでいます。これに対し、もし40℃、60℃、80℃という反応温度が無限母集団からランダムに選んだものであり、この場合選ばれた反応温度因子の水準がたまたま偶然に40℃、60℃、80℃という反応温度であったということであれば、このような因子のことを「変量型」因子と呼びます。したがって、変量型因子の実験においては、各反応温度における反応収率そのものには関心はなく、ただ反応温度をふった場合に反応収率がどの程度ばらつくのかということだけが興味の対象となっているわけです。実験に取り上げた因子にはその特徴を規定するための構造上のモデル（模型）を設定しなければならず、そのようなモデルのことを「構造モデル」と呼んでいます。したがって、構造モデルには「母数型モデル」と「変量型モデル」があることになります。

　さて、上述の例は一般的には「母数型１元配置実験」と考えるのが妥当なので、まずそれについて考えることにします。いま、40℃（因子Aの水準1に相当する）という反応温度条件下における反応収率の結果は繰り返しの数だけの個数あるわけですが、その各々のデータをとすれば、これらの値は、偶然誤差による分散である母平均の無限正規母集団からのランダムサンプルの実現値とみることができます。すなわち水準1内（級内）における実験誤差（偶然誤差）をとすれば

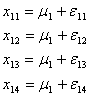
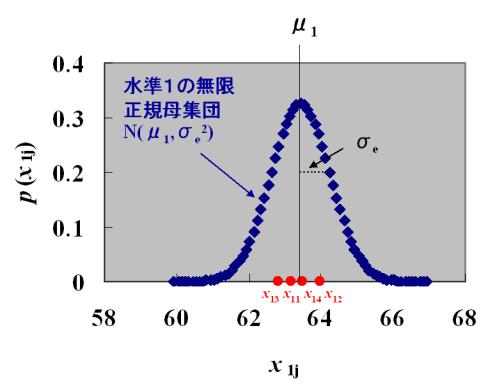
のように水準1の各データを書き表すことができます。つまり各データは無限正規母集団の母平均のまわりに母分散をもってばらついていることになります。比較のために水準１のデータのみを使って推定した無限正規母集団の確率密度関数も一緒に示しました。

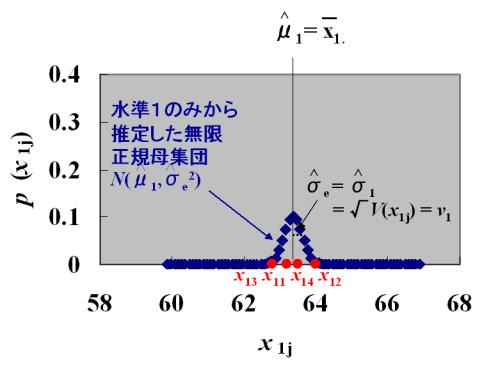
　これを、データの一般式（：因子Aの水準；：水準内の繰り返し番号）について表せば

となります。ここで、は因子Aの水準において想定した無限母集団の分布に従って変化する量であり、各実験条件における偶然誤差に相当します。通常、管理された実験においてはこのような実験誤差分布は正規分布をしていることがわかっているので、偶然誤差の母平均は0、母分散はと定義すれば

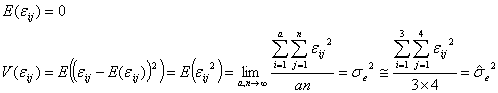
となります。この意味するところは実験誤差が無限正規母集団からのランダム・サンプリング（無作為抽出）であるということです。また、下図に見るように、実験全体（母集団）の母平均をとすれば、因子Aの各水準の平均値は母平均のまわりにばらついています。すなわち

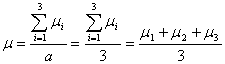
と定義し、

また、

と定義すれば、因子Aの番目の水準の効果、すなわち、は全平均に対する各反応温度条件のカタヨリ（bias）を表しており、これを主効果（main effect）と呼んでいます。ここで、上述の定義式より

の関係が成り立ちます。このように、因子Aの各水準を技術的に指定することができ、が一定の値をとると考えられる場合の実験の構造を特に「母数モデル」と呼んでいます。

　したがって、この実験の数学モデルは

のような線型モデルとなります。ここで、は因子Aの各水準（水準数）の母平均から個々のデータに至るカタヨリを意味します。また、はこのような偶然誤差であるのでその期待値はとなります。そこで、その分散をとすれば

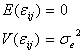
と書き表すことができます。いま、因子Aの各水準の誤差分散をと定義すれば

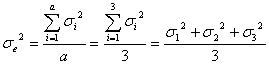
となります。したがって、偶然誤差の母分散の推定値は

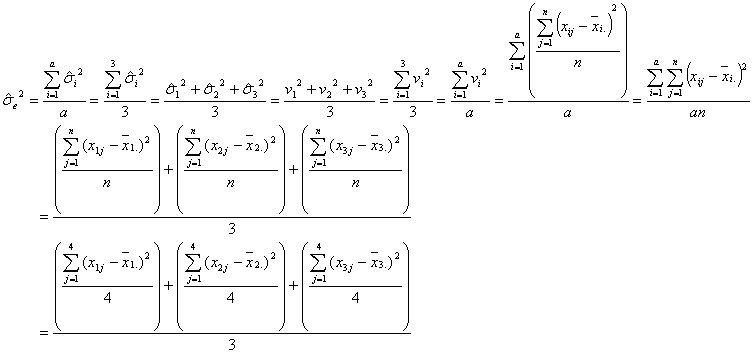
であり、因子Aの各水準（水準数）の母平均の推定値は

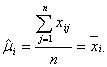
であり、この系全体の母平均の推定値は

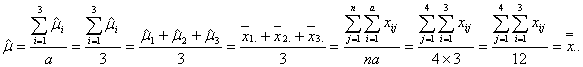
のようにして求めることができます。

　ここまででは個々のデータの構造を求めましたが、１元配置実験の分散分析を行うためには変動計算の基となる因子Aの水準毎の平均値と総平均値を知る必要があります。まず、水準の4個のデータをその構造式で表すと

となります。したがって、水準の平均値は

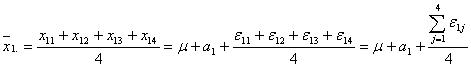
となりますが、右辺の第３項は水準内における実験誤差の平均値なので、これをと表すと

となります。さらに、この構造式を一般化すれば、水準の平均値は

と書き表すことができます。ところで、偶然誤差の総和は0ですから

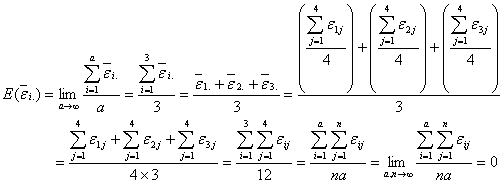
となります。また

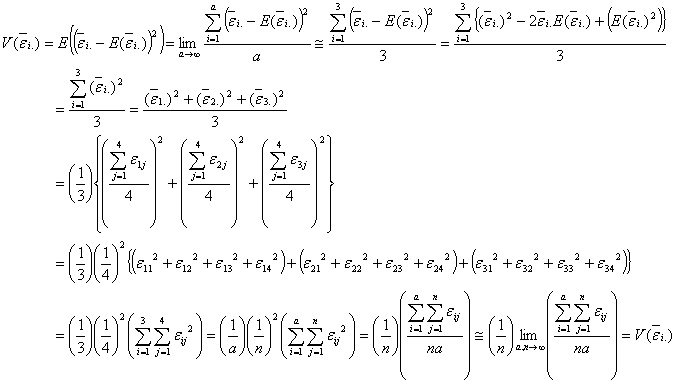
となりますが、冒頭の

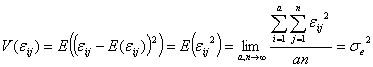
という定義式と見比べれば、求める分散は

となります。すなわち、因子Aの水準の平均値は無限正規母集団からの無作為抽出標本であることがわかります。

　次に総平均値についてその変動の期待値と分散を調べてみることにします。総平均値は

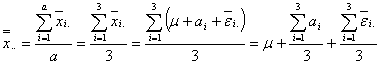
のようになるが、母数型モデルでは右辺第２項は0であり、また第３項は実験誤差の総平均なので、これをとおけば

となります。もし、実験系の因子Aがが母数型ではなく変量型である場合は

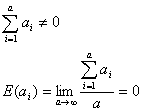
であるから

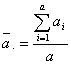
と定義すれば

のようになります。

　いずれにしても、誤差の総平均値はデータ１個当たりの誤差の総平均であるから

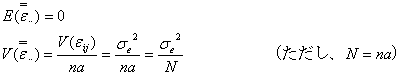
となり、総平均値は無限正規母集団あるいはからの無作為抽出標本であると結論することができます。