尤度関数と最尤推定値
池に何尾魚がいるかを調べるために、ある日100尾を捕獲し目印を付けてから放し、しばらく間をおいてからまた100尾を捕獲してみたところ、その中に先日目印を付けた魚が10尾見つかりました。このデータから池には何尾の魚がいると推定できるでしょうか。この問題を解くには「超幾何分布」を応用するのがよいと思われますが、そのために、この問題を一般化することにします。すなわち

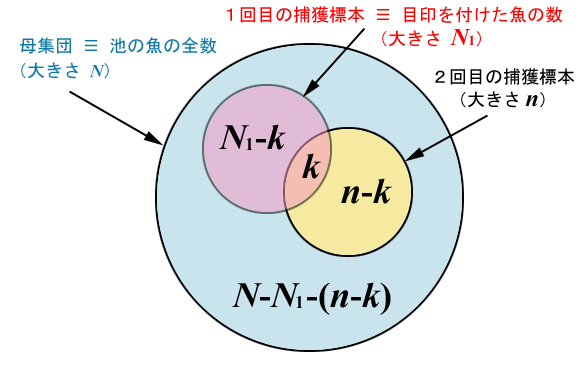
のようにしますと、この標本の確率変数![]() の確率
の確率![]() は次のような超幾何分布にしたがって
は次のような超幾何分布にしたがって
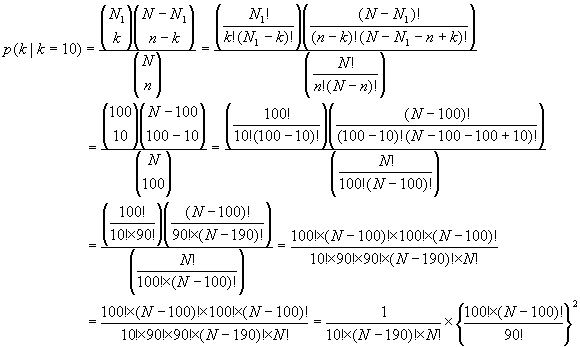
のようになります。この式から池の魚の全数![]() を求めたいわけが、確率
を求めたいわけが、確率![]() の値がわからない限り求まりそうにもありません。そこで、ここから推定をしなければなりません。まず、いま現在わかっているだけの状況を考えると
の値がわからない限り求まりそうにもありません。そこで、ここから推定をしなければなりません。まず、いま現在わかっているだけの状況を考えると

の合計の数だけの魚が池には最低限いることになります。したがって、その数![]() は
は
![]()
となります。それでは、この魚の数![]() だけ池にいたとすると、確率
だけ池にいたとすると、確率![]() はどれくらいになるか計算してみましょう。求める確率
はどれくらいになるか計算してみましょう。求める確率![]() は
は

となりますが、このままでは大変な計算になるので、スターリングの近似公式
![]()
を使って計算すると
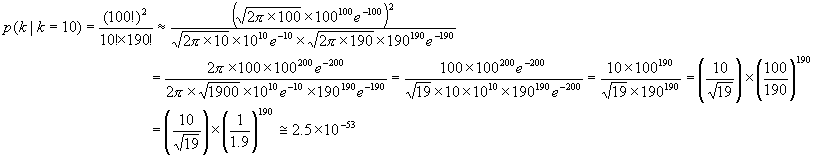
となります。この確率の値はいくら推定値とはいえあまりにも小さ過ぎて現実味に乏しいと思われます。そこで、任意のある観測値![]() に対して確率
に対して確率![]() を最大にする母数
を最大にする母数![]() の推定値
の推定値![]() を求めようとする方法「最尤法」(あるいは「最尤推定法」(method of maximum likelihood estimation)とも言います)がフィッシャーによって提案されています。この方法では推定値
を求めようとする方法「最尤法」(あるいは「最尤推定法」(method of maximum likelihood estimation)とも言います)がフィッシャーによって提案されています。この方法では推定値![]() のことを特に「最尤推定値」(maximum
likelihood estimate)と呼んでいます。意味は最も尤もらしい推定値ということです。この方法では
のことを特に「最尤推定値」(maximum
likelihood estimate)と呼んでいます。意味は最も尤もらしい推定値ということです。この方法では![]() を固定して母数
を固定して母数![]() を変数とするわけですから、
を変数とするわけですから、![]() を
を![]() あるいは
あるいは![]() と書き直すことにします。すなわち、対象とする関数
と書き直すことにします。すなわち、対象とする関数![]() は
は

で、この関数のことを「尤度関数」(likelihood function)と呼んでいます。最尤法では通常尤度関数![]() を最大ならしめるために
を最大ならしめるために![]() の偏微分方程式(尤度方程式)を解けばいいのですが、この例の場合は母数
の偏微分方程式(尤度方程式)を解けばいいのですが、この例の場合は母数![]() が整数であるため、尤度方程式を解いて求めることができません。
が整数であるため、尤度方程式を解いて求めることができません。
そこで、次のような比
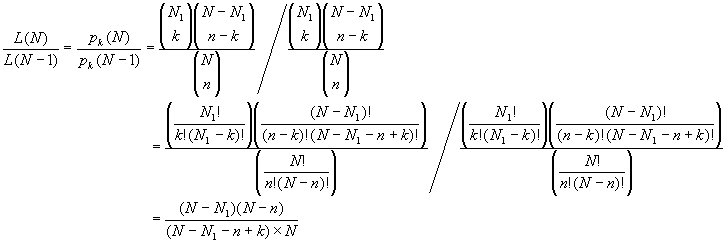
を考えると、![]() となるような最尤推定値
となるような最尤推定値![]() は
は
![]()
となるような関係を満たす最大の整数であることがわかります。
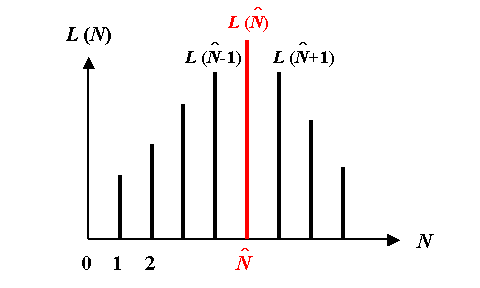
したがって、この条件式を上の比に代入すれば
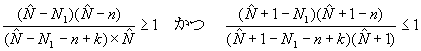
となり、これを変形すれば
![]()
となります。したがって、
![]()
となる整数が求める母数![]() (池の魚の全数)の最尤推定値となります。最後の数式の
(池の魚の全数)の最尤推定値となります。最後の数式の![]() の記号はガウスの記号で、左辺の値はカギ括弧内の数を超えない最大の整数を表すものとします。
の記号はガウスの記号で、左辺の値はカギ括弧内の数を超えない最大の整数を表すものとします。
そこで、本題の条件

を最尤推定値![]() に代入すれば、求める池の魚の最尤推定値
に代入すれば、求める池の魚の最尤推定値![]() は
は
![]()
となります。このようにして、求められた池の魚の最尤推定値![]() を使って、その確率
を使って、その確率![]() を求めてみますと
を求めてみますと

のようになります。
(参考)最尤法
「最尤法」あるいは「最尤推定法」は、母数の点推定をする一つの方法であるが、これは母集団の分布の形がわかっているがその母数が未知であるときに、標本値からその母数を決めようとする方法です。
いま母集団から大きさ![]() の標本を無作為抽出したとき、その標本の値が
の標本を無作為抽出したとき、その標本の値が![]() であったとします。すなわち、これは母集団分布に従う確率変数
であったとします。すなわち、これは母集団分布に従う確率変数![]() が実現値としてそれぞれ
が実現値としてそれぞれ![]() という値をとったことを意味します。ところで、標本変量
という値をとったことを意味します。ところで、標本変量![]() の確率密度関数(分布が離散型の場合は確率関数)は、母集団分布が
の確率密度関数(分布が離散型の場合は確率関数)は、母集団分布が![]() で与えられ、確率変数
で与えられ、確率変数![]() が互いに独立であるならば、一般に
が互いに独立であるならば、一般に
![]()
のような確率密度関数の積の形で与えられます。ここで![]() は確率変量
は確率変量![]() の実現値であり変数ですが、
の実現値であり変数ですが、![]() は一般に母数のような特性値ですから未知の定数です。しかしながら、いったん母集団から標本が抽出されてしまえば、実現値
は一般に母数のような特性値ですから未知の定数です。しかしながら、いったん母集団から標本が抽出されてしまえば、実現値![]() は定まった値として固定されてしまうことになり、一方、
は定まった値として固定されてしまうことになり、一方、![]() は未知数のままです。したがって、母数
は未知数のままです。したがって、母数![]() の推定量
の推定量![]() を求めるためには、
を求めるためには、![]() を
を![]() の関数と考えて
の関数と考えて
![]()
という![]() が固定で
が固定で![]() が変数となる新しい関数
が変数となる新しい関数![]() を考えます。この関数のことを「尤度関数」(likelihood function)あるいは単に「尤度」(likelihood)と呼び、この関数を用いて、
を考えます。この関数のことを「尤度関数」(likelihood function)あるいは単に「尤度」(likelihood)と呼び、この関数を用いて、![]() 固定の条件の下で、母数
固定の条件の下で、母数![]() の最も尤もらしい点推定により母数の推定量あるいは推定値である
の最も尤もらしい点推定により母数の推定量あるいは推定値である![]() を求めようとするのが「最尤法」です。
を求めようとするのが「最尤法」です。
この尤度関数を最大にする推定値![]() のことを「最尤推定値」(maximum
likelihood estimate)と呼び、
のことを「最尤推定値」(maximum
likelihood estimate)と呼び、![]() のことを「最尤推定量」(maximum
likelihood estimator)と呼び、最尤法はこの
のことを「最尤推定量」(maximum
likelihood estimator)と呼び、最尤法はこの![]() を求める方法になります。ここで、
を求める方法になります。ここで、![]() あるいは
あるいは![]() の
の![]() は「統計量」(statistic)を意味します。したがって
は「統計量」(statistic)を意味します。したがって
![]()
を解けば最尤推定値あるいは最尤推定量である![]() が求められることになります。尤度関数
が求められることになります。尤度関数![]() は積関数で計算が面倒なので、尤度関数の対数をとった新しい関数
は積関数で計算が面倒なので、尤度関数の対数をとった新しい関数![]() 、すなわち
、すなわち
![]()
を定義し
![]()
を解いた方が便利なことが多いと考えられます。このような偏微分方程式のことを「尤度方程式」と呼ぶこともあります。
(例題1)正規母集団![]() から大きさ
から大きさ![]() の標本を無作為抽出したときの標本値が
の標本を無作為抽出したときの標本値が![]() でした。母分散
でした。母分散![]() が既知であるときの母平均
が既知であるときの母平均![]() の最尤推定量を求めてみましょう。ただし、正規母集団
の最尤推定量を求めてみましょう。ただし、正規母集団![]() の確率密度関数
の確率密度関数![]() は
は
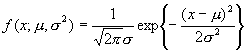
です。
標本値![]() は互いに独立なので、
は互いに独立なので、![]() の積をとることにより、標本変量
の積をとることにより、標本変量![]() の確率密度関数は
の確率密度関数は

のようになります。そこで、標本値![]() と母分散
と母分散![]() が一定で母平均
が一定で母平均![]() を変数とする尤度関数
を変数とする尤度関数![]() は
は

となります。ここで、計算を簡単にするため上式の対数をとれば

となるので、この![]() を最大にする
を最大にする![]() を求めるには
を求めるには

となる尤度方程式を解けばよい。したがって
![]()
すなわち
![]()
となり、最尤推定値![]() が求まりました。したがって、最尤推定量
が求まりました。したがって、最尤推定量![]() は
は
![]()
となります。すなわち、母分散![]() がわかっている場合の母平均
がわかっている場合の母平均![]() の最尤推定値
の最尤推定値![]() は不偏推定量に等しくなります。
は不偏推定量に等しくなります。
(例題2)正規母集団![]() から大きさ
から大きさ![]() の標本を無作為抽出したときの標本値が
の標本を無作為抽出したときの標本値が![]() でした。母分散
でした。母分散![]() が未知であるときの母平均
が未知であるときの母平均![]() の最尤推定量を求めてみましょう。ただし、正規母集団
の最尤推定量を求めてみましょう。ただし、正規母集団![]() の確率密度関数
の確率密度関数![]() は
は
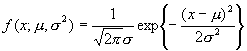
です。
標本値![]() は互いに独立なので、
は互いに独立なので、![]() の積をとることにより、標本変量
の積をとることにより、標本変量![]() の確率密度関数は
の確率密度関数は
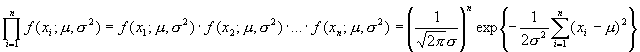
のようになります。そこで、標本値![]() を固定して母平均
を固定して母平均![]() と母分散
と母分散![]() を変数とする尤度関数
を変数とする尤度関数![]() は
は
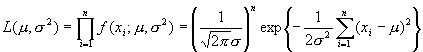
となります。ここで、計算を簡単にするため上式の対数をとれば

となるので、この![]() を最大にする
を最大にする![]() と
と![]() を求めるには、連立方程式
を求めるには、連立方程式
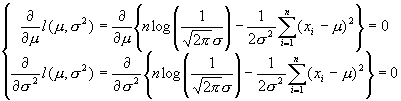
を解けばよい。したがって、最初の尤度方程式より
![]()
が求められるので、これと第2の尤度方程式により
![]()
が得られます。よって、母平均![]() と母分散
と母分散![]() の最尤推定量
の最尤推定量![]() と
と![]() は、それぞれ
は、それぞれ
![]()
および
![]()
となります。この尤度法で得られた最尤推定量![]() は母平均
は母平均![]() の不偏推定量であるが、最尤推定量
の不偏推定量であるが、最尤推定量![]() は母分散
は母分散![]() の不偏推定量とはなっていません。すなわち
の不偏推定量とはなっていません。すなわち
![]()
なので、最尤推定量![]() を母分散
を母分散![]() の不偏推定量とするためには、
の不偏推定量とするためには、
![]()
のように分母を![]() にする必要があります。もちろん標本の大きさ
にする必要があります。もちろん標本の大きさ![]() がかなり大きいときは、尤度法でも母分散
がかなり大きいときは、尤度法でも母分散![]() にきわめて近い(偏りがない)推定量が求められることになります。
にきわめて近い(偏りがない)推定量が求められることになります。