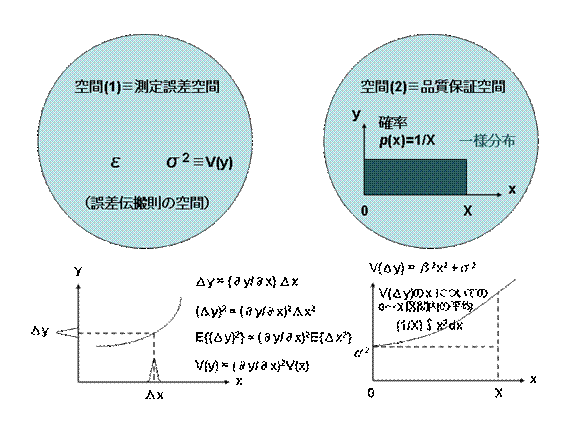
表示値と分散（回帰直線近似標本）

母回帰線近似標本（）について、その表示値をとしたときの分散をとすれば

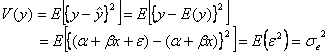
となります。この分散の式を導くのに、標本回帰直線（）を使って導出すれば

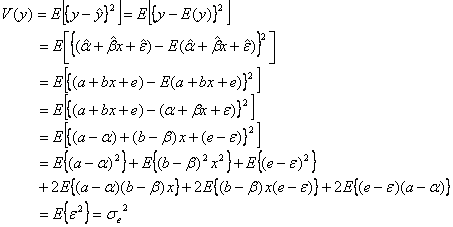
のように結局母回帰直線モデルから導出した分散に一致します（証明略）。

また、母回帰線近似標本（）について、その表示値を平均としたときの分散をとすれば

さらに、母回帰線近似標本（）について、その表示値を切片としたときの分散をとすれば

　一方、母回帰線近似標本（）のの区間の任意のの値を表示値（ただし、このときの表示値は質量比混合法で調製した誤差を伴わない真値であると仮定する）で保証する場合の分散を見積もってみることにします。

であるので、残差の期待値（母平均）は

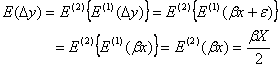
となります。したがって、求める分散は

となります。この導出過程では品質保証期間内のカタヨリの期待値（平均）を

と置いたが、品質保証期間内のすべてにおいて表示値を保証するというふうに考えれば、その期待値（平均値）は原点と置くのが普通の考え方であろう。したがって、その場合の表示値に付すべき分散は

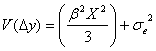
となります。品質保証期間内のすべてにおいて表示値を保証するこの分散の中で品質保証期間内の不確かさにのみ関連する分散をとすれば

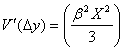
であるから、その標準不確かさをと定義すれば

となります。また、この場合の拡張不確かさは、一様分布の概念からは

となりますが、一様分布とは関係なく通常の標準不確かさから拡張不確かさを見積もるというのであれば、一般的な包含係数を用いて

と表記するのが分かり易くてよいでしょう。

（参考）上述の分散の導出過程で期待値の記号にとの２通りがありますが、１つ目は通常の測定誤差空間での期待値あるいは分散に関わる項であり、２つ目は品質保証期間内の空間における期待値あるいは分散に関わる項で、統計的には別の空間に属します。