分銅のパラドックス（強い相関の例）

　いま表示値が500gの分銅が2個あり、いずれも不確かさが1%であったとします。そこでこの分銅2個を組にして天秤で校正しながらもう１つ別の分銅（表示値1kg）を製作したときに得られる1kgの分銅の不確かさはどうなるでしょうか。

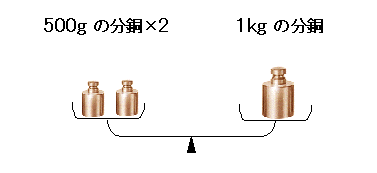
　２つの500gの分銅の真値をおよびとし、表示値をおよびとすれば

となります。ここで、およびは重さのバラツキです。一方、1kgの分銅の真値を、その表示値をとすれば

となります。したがって、1kgの分銅の表示値の不確かさは

となります。よって、求める1kgの分銅の不確かさ（変動係数）は

となり、もとになった500g分銅の不確かさ1%よりもはるかに精度のよい1kgの分銅すなわち0.7%の不確かさの分銅が得られたことになり、明らかにおかしい。これを「分銅のパラドックス」と呼んでいます。

　このようなパラドックスが生じた原因は２個の500gの分銅のバラツキが互いに無関係（相関のない）な独立な不確かさとみなして1kgの分銅の不確かさを合成したのであるが、実際には両者の分銅の間には強い相関（相関係数）があると考えれば、求める不確かさの合成値は、相関がある場合の不確かさの伝搬則

ここで、相関係数は

であり、また

あるとします。

を適用することにより

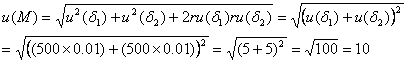
となります。したがって、求める1kgの分銅の不確かさ（変動係数）は

となり、1kgの分銅の不確かさも１％となり、現実に即したものとなります。