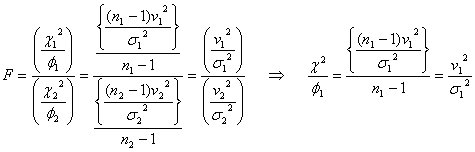F分布
![]() 分布(F-distribution)は、正規分布、
分布(F-distribution)は、正規分布、![]() 分布、
分布、![]() 分布などと並んで、推測統計や不確かさを論じる上で極めて重要な分布であり、いま自由度がそれぞれ
分布などと並んで、推測統計や不確かさを論じる上で極めて重要な分布であり、いま自由度がそれぞれ![]() であるカイ二乗変数
であるカイ二乗変数![]() と
と![]() が互いに独立であるとき、その比
が互いに独立であるとき、その比
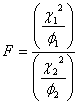
は![]() 分布をします。
分布をします。![]() 分布はまたスネデカーの
分布はまたスネデカーの![]() 分布(Snedecor’s
F-distribution)あるいはフィッシャー分布(Fisher
distribution)とも呼ばれます。
分布(Snedecor’s
F-distribution)あるいはフィッシャー分布(Fisher
distribution)とも呼ばれます。
この分布の確率密度関数![]() は次式で与えられ、その出現確率は自由度
は次式で与えられ、その出現確率は自由度![]() と
と![]() によって特徴づけられます。
によって特徴づけられます。
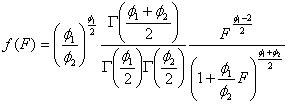
あるいは

ただし、
![]()
をベータ関数と言います。ベータ関数は、![]() が整数の場合(それぞれ
が整数の場合(それぞれ![]() とする)は
とする)は
![]()
という性質を持っています。


また、変数![]() の逆数である
の逆数である![]() も自由度
も自由度![]() で特徴づけられる
で特徴づけられる![]() 分布をすることから、変数
分布をすることから、変数![]() の分母子の取り方はどちらをとってもよいのであるが、通常分子が大きくなるように変数
の分母子の取り方はどちらをとってもよいのであるが、通常分子が大きくなるように変数![]() を選ぶ場合が多い。
を選ぶ場合が多い。
ところで、カイ二乗変数![]() と
と![]() は2つの正規母集団
は2つの正規母集団![]() と
と![]() からそれぞれ互いに独立に抽出した大きさがそれぞれ
からそれぞれ互いに独立に抽出した大きさがそれぞれ![]() の標本(不偏分散はそれぞれ
の標本(不偏分散はそれぞれ![]() )に相当するものであるから、変数
)に相当するものであるから、変数![]() は
は
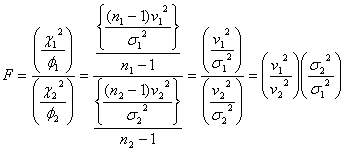
のように変形でき、母数として母平均に関係なく母分散のみを含む式となります。
いま、2つの正規母集団の母分散が等しい(![]() )ならば、上式は2つの標本の不偏分散比のみの関係式となり、これが
)ならば、上式は2つの標本の不偏分散比のみの関係式となり、これが![]() 分布をすることになります。
分布をすることになります。
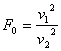
この関係式は2つの正規母集団の分散が等しいかどうかを検定するのに用いることができる非常に便利でかつ重要な関係式で、分散分析などの統計処理においてもしばしば用いられます。
そこで、ここでは![]() 分布を用いた2つの正規母集団の分散の検定方法を紹介することにします。いま、2つの正規母集団
分布を用いた2つの正規母集団の分散の検定方法を紹介することにします。いま、2つの正規母集団![]() と
と![]() に対して、
に対して、
帰無仮説![]() および対立仮説
および対立仮説![]()
をたてます。この帰無仮説が正しければ、
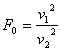
は自由度![]() の
の![]() 分布をすることになるので、2つの標本の不偏分散比から算出した
分布をすることになるので、2つの標本の不偏分散比から算出した![]() を有意水準
を有意水準![]() における
における![]() 分布の理論値
分布の理論値![]() とを比較します。もし、このとき、
とを比較します。もし、このとき、
![]()
ならば、帰無仮説は危険率![]() で棄却され、対立仮説
で棄却され、対立仮説![]() を採択することになり、
を採択することになり、
![]()
ならば、帰無仮説![]() は棄却できず、2つの母集団は等分散である可能性が高いと言えます。
は棄却できず、2つの母集団は等分散である可能性が高いと言えます。
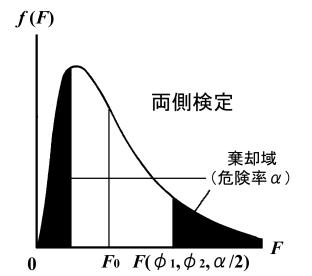
この場合は両側検定となるので、![]() は、
は、![]() と比較するのではなく、
と比較するのではなく、![]() と比較しなければなりません。
と比較しなければなりません。
一方、何らかの知見からあらかじめ母分散![]() の方が母分散
の方が母分散![]() よりも大きいことがわかっている場合には、あるいは対立仮説として
よりも大きいことがわかっている場合には、あるいは対立仮説として![]() を予測する場合は、帰無仮説
を予測する場合は、帰無仮説![]() に対して
に対して
対立仮説![]()
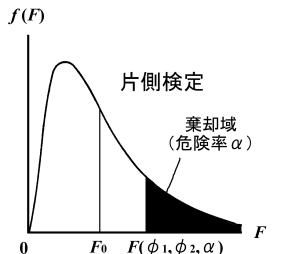
を検定することになり、このときは上図のような片側検定(右側検定あるいは上側検定)となります。すなわち、2つの標本の不偏分散比から算出した![]() を有意水準
を有意水準![]() における
における![]() 分布の理論値
分布の理論値![]() とを比較します。もし、このとき、
とを比較します。もし、このとき、
![]()
ならば、帰無仮説は危険率![]() で棄却され、対立仮説
で棄却され、対立仮説![]() を採択することになり、
を採択することになり、
![]()
ならば、帰無仮説![]() は棄却できず、2つの母集団は等分散である可能性が高いと言えます。
は棄却できず、2つの母集団は等分散である可能性が高いと言えます。
また、上とは逆に、対立仮説として![]() をとるときには、棄却域は
をとるときには、棄却域は
![]()
のような片側検定(左側検定あるいは下側検定)となります。
確率変数![]() が
が![]() 分布すなわち
分布すなわち![]() に従うときには、次のような特徴があります。
に従うときには、次のような特徴があります。
まず、確率変数![]() の平均
の平均![]() と分散
と分散![]() は
は

となります。また、確率変数![]() の逆数
の逆数![]() は
は![]() に従います。さらに、
に従います。さらに、![]() の右側
の右側![]() 点は
点は![]() の左側
の左側![]() 点の逆数に相当します。すなわち
点の逆数に相当します。すなわち
![]()
という関係が成立します。
![]() 分布の自由度
分布の自由度![]() のうち自由度
のうち自由度![]() が十分大きくなれば、
が十分大きくなれば、![]() 分布は自由度
分布は自由度![]() の
の![]() 分布に従う量を自由度
分布に従う量を自由度![]() で割ったものの分布によって近似できることが知られています。
で割ったものの分布によって近似できることが知られています。