不偏分散の期待値の求め方

不偏分散の期待値を求めるのは結構面倒ですが、根気よく計算すれば不偏分散から期待値が求められることを、次のような「一元配置実験モデル」で例示します。下表は「一元配置実験モデル」（変動要因の水準数個、繰り返し測定回数個の標本モデル、実測値の確率変数をとする）で、その実測値と確率変数は

のようになります。ただし、主効果の母平均はでその母分散は、また偶然誤差の母平均はでその母分散はとします。

列平均　　　

列分散　　　

一元配置実験標本についての構造モデル

から、標本データの不偏分散との期待値は、それぞれ

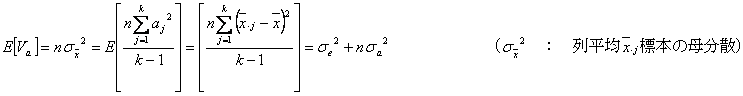
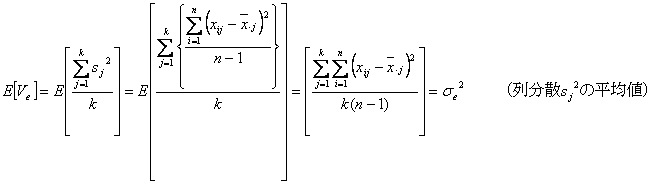
となることが知られているが、この期待値の求め方を以下詳述します。それには上述の標本の構造モデルの代わりに母集団の構造モデル式

から出発した方が簡単なのでそのようにします。

上式のについての平均をとれば

となり、また、繰り返し測定変動誤差の偏差平方和は

となります。そこで、この期待値を計算してみると

となります。

　一方、繰り返し測定誤差変動の不偏分散は

であると定義されているので、不偏分散の期待値は

となります。

　次に、変動要因の偏差平方和は

であるから、その期待値を計算してみると、（主効果）と（偶然誤差）は独立な誤差であることを考慮して、

となります。したがって、変動要因の偏差平方和の不偏分散は

であるから、その期待値は

となります。