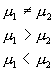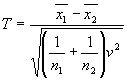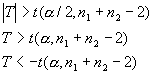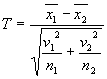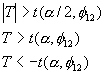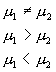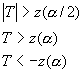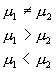測定比較スキームEn
ある標準物質について2つの試験機関の間でどの程度測定値の一致度がいいかを見るために、![]() という物差しで評価を行うことがあります。この
という物差しで評価を行うことがあります。この![]() という統計量は次のように定義されます。いま、機関Aと機関Bの測定値のそれぞれの平均を
という統計量は次のように定義されます。いま、機関Aと機関Bの測定値のそれぞれの平均を![]() および
および![]() とし、またそれぞれの標本平均の拡張不確かさ
とし、またそれぞれの標本平均の拡張不確かさ![]() および
および![]() とすれば、
とすれば、![]() は
は

となります。ここで、機関Aと機関Bのそれぞれの平均![]() および
および![]() の標準不確かさをそれぞれ
の標準不確かさをそれぞれ![]() および
および![]() と定義すれば
と定義すれば
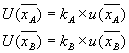
となります。ただし、![]() および
および![]() は包含係数(coverage
factor)と呼ばれるもので、標準不確かさ
は包含係数(coverage
factor)と呼ばれるもので、標準不確かさ![]() および
および![]() を算出するのに用いた自由度の
を算出するのに用いた自由度の![]() -分布の値から得られる値であるが、ここでは大標本で一般的によく用いられる包含係数値
-分布の値から得られる値であるが、ここでは大標本で一般的によく用いられる包含係数値![]() を採用することにします。そうすると上式は
を採用することにします。そうすると上式は

のように簡単な式となります。この関係を![]() の定義式に代入すると
の定義式に代入すると

となります。一方、機関Aおよび機関Bの不偏分散を![]() (標本数
(標本数![]() 個)および
個)および![]() (標本数
(標本数![]() 個)とすれば、標準偏差は
個)とすれば、標準偏差は
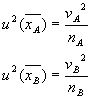
ですから、![]() は
は
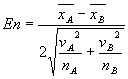
![]()
と書くこともできます。
このように2つの試験機関の間での測定比較スキーム(技能試験)においては![]() は重要な意味を持ち、その結果は以下のように判定されます。
は重要な意味を持ち、その結果は以下のように判定されます。

この関係は、それぞれの母平均が![]() と
と![]() でまたそれぞれの母分散が
でまたそれぞれの母分散が![]() および
および![]() である2つの正規母集団から抽出した2つの標本の平均
である2つの正規母集団から抽出した2つの標本の平均![]() (標本数
(標本数![]() )と
)と![]() (標本数
(標本数![]() )の差
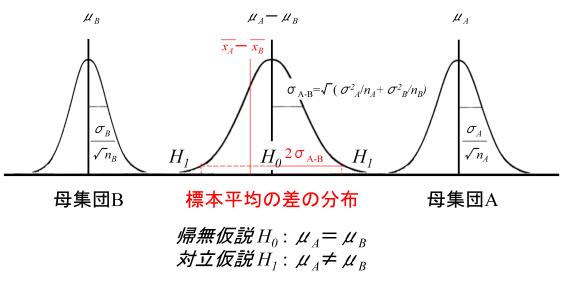
)の差![]() が偶然誤差でなく意味のある差になっているのかどうかを検定するための統計手法と似ています。すなわち、後者では、一般に帰無仮説として2つの母平均には差がない(
が偶然誤差でなく意味のある差になっているのかどうかを検定するための統計手法と似ています。すなわち、後者では、一般に帰無仮説として2つの母平均には差がない(![]() )とするから、その帰無仮説検定量は
)とするから、その帰無仮説検定量は

と定義され、変数![]() は平均が
は平均が![]() 、分散が
、分散が![]() の正規分布に従うことから、近似的には自由度
の正規分布に従うことから、近似的には自由度![]() の
の![]() 分布に従うことになりますが、
分布に従うことになりますが、![]() は式の上ではこの
は式の上ではこの![]() と同じ関係になります。ただし、自由度
と同じ関係になります。ただし、自由度![]() はSatterthwaite(サタースウェイト)の方法により、次式の通り求められます。
はSatterthwaite(サタースウェイト)の方法により、次式の通り求められます。

この自由度![]() を標準誤差和
を標準誤差和![]() の等価自由度とも呼ばれます。
の等価自由度とも呼ばれます。
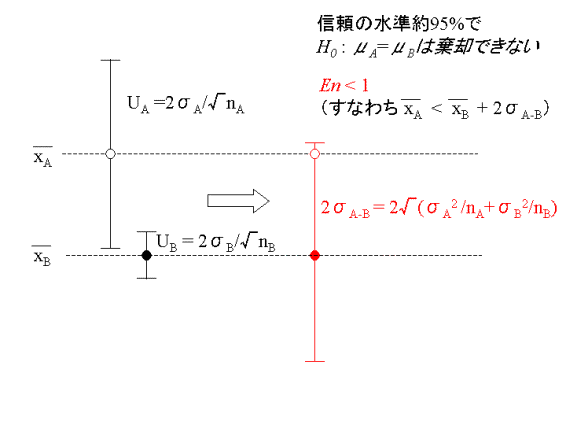
したがって、![]() の判定式は2つの標本平均の差の帰無仮説の検定で信頼区間を標準誤差
の判定式は2つの標本平均の差の帰無仮説の検定で信頼区間を標準誤差![]() 2個分、すなわち、信頼の水準を約95%にした場合に相当することになります。
2個分、すなわち、信頼の水準を約95%にした場合に相当することになります。
《参考:正規母集団![]() と
と![]() の等平均仮説の検定》
の等平均仮説の検定》
いま、正規母集団が2つ(![]() )あり、それぞれのデータ数が
)あり、それぞれのデータ数が![]() 個である場合を考え、その各々のデータが
個である場合を考え、その各々のデータが![]() であるとすれば、それぞれの標本平均
であるとすれば、それぞれの標本平均![]() 、標本分散
、標本分散![]() 、および不偏分散
、および不偏分散![]() は
は
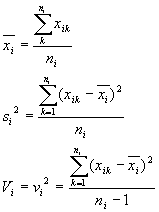
となります。したがって、標本分散![]() と不偏分散
と不偏分散![]() および偏差平方和
および偏差平方和![]() の間には
の間には
![]()
のような関係式が成り立ちます。
さて、上記の関係式の前提として母平均![]() と母分散
と母分散![]() があらかじめわかっている2つの正規母集団
があらかじめわかっている2つの正規母集団![]() と
と![]() を仮定したが、正規母集団の母数については何もわかっていない場合や母集団が正規分布でない場合も現実問題として起こりえます。そこで、これらすべての場合について2つの母集団の平均の差の検定をどのようにして行うのかを以下場合分けして調べることにします。
を仮定したが、正規母集団の母数については何もわかっていない場合や母集団が正規分布でない場合も現実問題として起こりえます。そこで、これらすべての場合について2つの母集団の平均の差の検定をどのようにして行うのかを以下場合分けして調べることにします。
(1) 正規母集団![]() と
と![]() で、母分散
で、母分散![]() が共に既知である場合
が共に既知である場合
|
|
|
統計量 |
分布 |
棄却域 |
|
|
|
|
|
|
(2) 正規母集団![]() と
と![]() で、母分散
で、母分散![]() が共に未知ではあるが、
が共に未知ではあるが、![]() は既知である場合
は既知である場合
|
|
|
統計量 |
分布 |
棄却域 |
|
|
|
|
|
|
ここで、不偏分散![]() です。
です。
(3)正規母集団![]() と
と![]() で、母分散
で、母分散![]() が共に未知、
が共に未知、![]() も未知である場合
も未知である場合
|
|
|
統計量 |
分布 |
棄却域 |
|
|
|
|
|
|
ここで、![]() 分布の自由度
分布の自由度![]() は次式で与えられます。
は次式で与えられます。
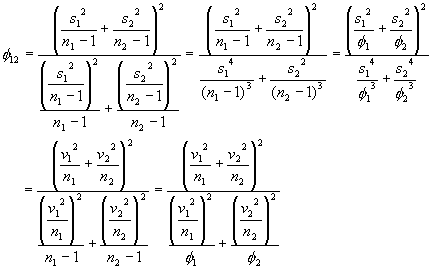
(4)2つの母集団分布は未知だが、どちらも大標本である場合
|
|
|
統計量 |
分布 |
棄却域 |
|
|
|
|
近似的に |
|
ここで、![]() は2つの母集団の標本分散です。
は2つの母集団の標本分散です。
(5)正規母集団![]() と
と![]() からの標本の大きさが等しく対応があり、
からの標本の大きさが等しく対応があり、![]() が既知である場合
が既知である場合
|
|
|
統計量 |
分布 |
棄却域 |
|
|
|
|
|
|
ここで、![]() は標本の大きさです。また、母分散
は標本の大きさです。また、母分散![]() は
は
![]()
です。ただし、偏差![]() とその平均
とその平均![]() は
は
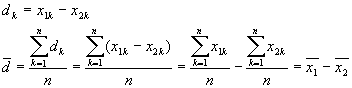
です。
(6)正規母集団![]() と
と![]() からの標本の大きさが等しく対応があり、
からの標本の大きさが等しく対応があり、![]() が未知である場合
が未知である場合
|
|
|
統計量 |
分布 |
棄却域 |
|
|
|
|
|
|
ここで、![]() は標本の大きさです。また、不偏分散
は標本の大きさです。また、不偏分散![]() は
は
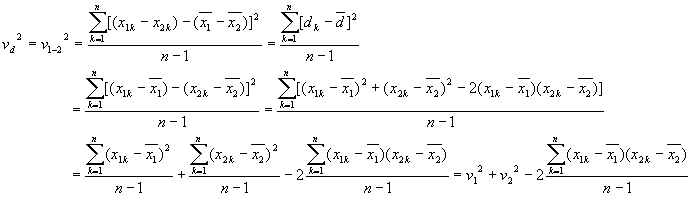
です。