母分散と不偏分散
ある観測対象全体の集合を母集団(population)と呼び、その母集団の中からいくつかを選んで観測した対象を標本(sample)と呼びます。

ある工場で製造した製品を出荷する場合には、その製品が正しい規格になっているかどうかをチェックする必要がありますが、電球の寿命のように全数チェックするわけにはいかない場合が多い。なぜなら、全数チェックするとなると出荷予定の蛍光灯を全部寿命のくるまで点灯検査するわけですから、検査が終わったものは球切れしていて出荷できないという矛盾が起こります。そこで、このような品質管理においては、母集団(この場合ある工場が製造している製品のすべて)の全数調査ではなく、その母集団からランダムに選んだ製品のいくつか(標本)のみを規格内に収まっているかどうかをチェックする場合が普通です。そして、この標本から得られる特徴(統計量)から母集団の特徴を表す母数(母平均と母分散)を推定し、品質管理に役立てるわけです。品質管理にとどまらず統計調査にはこのような母集団と標本の関係がいつでも成立します。近年では、このように標本から母集団の特性値を推測する統計学を「推測統計学」と呼んでいます。
いま、標本は![]() 個の観測値(
個の観測値(![]() )から成り、母集団はそれよりも大きい
)から成り、母集団はそれよりも大きい![]() 個の観測値(
個の観測値(![]() )から成るものとします。ここで、母集団の
)から成るものとします。ここで、母集団の![]() 個の観測値の中で標本に相当する
個の観測値の中で標本に相当する![]() 個の観測値のみが実測値であり、残りの
個の観測値のみが実測値であり、残りの![]() 個の観測値は現実には測定しない個々の特性値です。そうすると、母集団のばらつきの度合いを示す母分散(
個の観測値は現実には測定しない個々の特性値です。そうすると、母集団のばらつきの度合いを示す母分散(![]() )は母平均を
)は母平均を![]() とすると
とすると
![]()
となります。一方、標本のばらつきの度合いを示す標本分散(![]() )については、母平均(
)については、母平均(![]() )がわからない場合が普通なので、母平均を標本平均(
)がわからない場合が普通なので、母平均を標本平均(![]() )で推定することにすれば、母集団と同じようにして
)で推定することにすれば、母集団と同じようにして
![]()
ここで、![]()
となるが、この標本分散は母分散の推定値にはならないことが統計学的に証明されており、次式で示されるような不偏分散(![]() )が母分散の正しい推定値となり得るとされています。ただし、母集団の個数
)が母分散の正しい推定値となり得るとされています。ただし、母集団の個数![]() は標本の個数
は標本の個数![]() に比べて極めて大きく無限に近いもの(このような母集団のことを無限母集団といいます)と仮定します。
に比べて極めて大きく無限に近いもの(このような母集団のことを無限母集団といいます)と仮定します。
![]()
標本の大きさが![]() なのに不偏分散の自由度が
なのに不偏分散の自由度が![]() であるのは、不偏分散を求める式の中の
であるのは、不偏分散を求める式の中の![]() 個の観測値(
個の観測値(![]() )がお互いに完全には独立ではなく、どれか一つの観測値は他の
)がお互いに完全には独立ではなく、どれか一つの観測値は他の![]() 個の独立な観測値と標本平均(
個の独立な観測値と標本平均(![]() )から求められるからです。
)から求められるからです。
母分散(![]() )と不偏分散(
)と不偏分散(![]() )の式の中で分母だけがこのように異なるのは一見奇異な感じがしますが、母集団の大きさnがかなり大きく、また標本の大きさ
)の式の中で分母だけがこのように異なるのは一見奇異な感じがしますが、母集団の大きさnがかなり大きく、また標本の大きさ![]() が
が![]() と同等までに大きくなった極限では、不偏分散が、母分散にほぼ一致し、母分散の良い推定値となります。
と同等までに大きくなった極限では、不偏分散が、母分散にほぼ一致し、母分散の良い推定値となります。
ところで、大きさ![]() の正規母集団
の正規母集団![]() から大きさ
から大きさ![]() の標本を取り出す取り出し方は
の標本を取り出す取り出し方は![]() 通りあるので、標本平均(
通りあるので、標本平均(![]() )もそれだけの数だけあることになります。この標本平均(
)もそれだけの数だけあることになります。この標本平均(![]() )をもとの正規母集団
)をもとの正規母集団![]() の正規分布曲線の上に重ねて描いてみると下図のようになり、標本平均(
の正規分布曲線の上に重ねて描いてみると下図のようになり、標本平均(![]() )が描く曲線も母平均を中心とした正規分布曲線となります。
)が描く曲線も母平均を中心とした正規分布曲線となります。
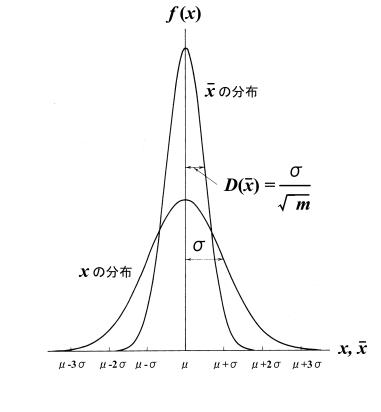
ただし、その正規分布の分散はもとの正規母集団![]() の母分散
の母分散![]() の
の![]() になることが知られています。すなわち、標本平均(
になることが知られています。すなわち、標本平均(![]() )の期待値、分散、標準偏差はそれぞれ
)の期待値、分散、標準偏差はそれぞれ
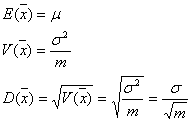
となります。この場合は、母集団がたまたま正規母集団![]() であったが、母集団が正規母集団でなくてその確率変数がどんな分布をしていても、標本の平均の分布は正規分布になることが知られており、これを「中心極限定理」と呼んでいます。また、平均と分散が有限な確率分布で最も起こりやすい(エントロピー極大の)分布は正規分布であるとされており、これを「エントロピー極大原理」と呼んでいます。このように、実際問題としては、確率変数そのものあるいはその平均がつくる分布は一般に正規分布であるとみなしてもよいと言えます。
であったが、母集団が正規母集団でなくてその確率変数がどんな分布をしていても、標本の平均の分布は正規分布になることが知られており、これを「中心極限定理」と呼んでいます。また、平均と分散が有限な確率分布で最も起こりやすい(エントロピー極大の)分布は正規分布であるとされており、これを「エントロピー極大原理」と呼んでいます。このように、実際問題としては、確率変数そのものあるいはその平均がつくる分布は一般に正規分布であるとみなしてもよいと言えます。
ところが、もしもとの正規母集団![]() が無限母集団(
が無限母集団(![]() )ではなく大きさ
)ではなく大きさ![]() の有限母集団であった場合には、上記の統計量(期待値と分散)は
の有限母集団であった場合には、上記の統計量(期待値と分散)は
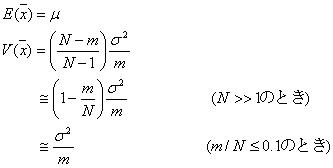
この係数![]() のことを有限補正(finite
population correction)と呼んでいるが、一般にわれわれが標本のサンプリングを行うときには有限母集団の
のことを有限補正(finite
population correction)と呼んでいるが、一般にわれわれが標本のサンプリングを行うときには有限母集団の![]() もサンプリングを行うようなことはまずあり得ないので標本平均(
もサンプリングを行うようなことはまずあり得ないので標本平均(![]() )の分散は無限母集団からのサンプリングの場合と同じく
)の分散は無限母集団からのサンプリングの場合と同じく
![]()
であると見なして差し支えありません。また、実際の統計処理においては母集団が無限母集団である場合も多いことから、有限補正(finite population correction)が必要になるケースは現実問題としてめったに起こりえないと言えます。