���v�I��������i�M����ԁA�M�����A�댯���A���o�́A���킨��ё���̉ߌ�j
�@�ꕽ�ς�![]() �ŕꕪ�U��
�ŕꕪ�U��![]() �̕�W�c����
�̕�W�c����![]() �̑傫���̔C�ӕW�{�𒊏o�����Ƃ��A��W�c���ǂ�ȕ��z�ł��낤�Ƃ�
�̑傫���̔C�ӕW�{�𒊏o�����Ƃ��A��W�c���ǂ�ȕ��z�ł��낤�Ƃ�![]() ���傫����i
���傫����i![]() �j���S�Ɍ��藝�ɂ��A���̕W�{����
�j���S�Ɍ��藝�ɂ��A���̕W�{����![]() �́A���}�̂悤�ɁA���ς�
�́A���}�̂悤�ɁA���ς�![]() �ŕ��U��
�ŕ��U��![]() �̐��K���z
�̐��K���z![]() �ɋߎ��ł��邱�Ƃ��m���Ă��܂��B
�ɋߎ��ł��邱�Ƃ��m���Ă��܂��B
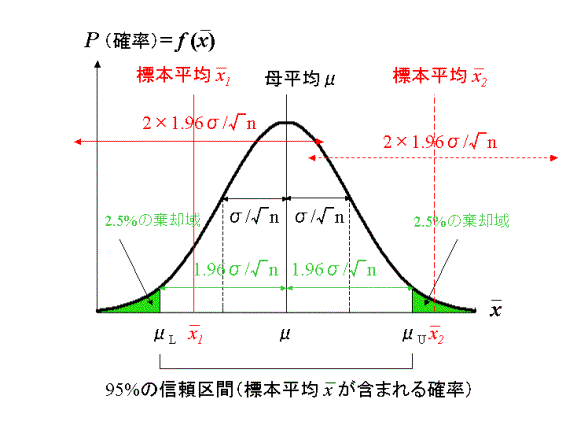
�@��}�Ō�����悤�ɁA��W�c���疳��ג��o�������傫��![]() �̕W�{�̕���
�̕W�{�̕���![]() �͕ꕽ��
�͕ꕽ��![]() �𒆐S�Ƃ���
�𒆐S�Ƃ���![]() �܂ŕ��z�����邱�Ƃ��킩��܂��B�������A�W�{����
�܂ŕ��z�����邱�Ƃ��킩��܂��B�������A�W�{����![]() �̒l���ꕽ��
�̒l���ꕽ��![]() ���痣���قǂ��̎����m��
���痣���قǂ��̎����m��![]() �͏������Ȃ�
�͏������Ȃ�![]() ��
��![]() �̋Ɍ��ł�
�̋Ɍ��ł�![]() �ƂȂ�A���̏ꍇ�͌����Ď������������Ȃ��W�{����
�ƂȂ�A���̏ꍇ�͌����Ď������������Ȃ��W�{����![]() �̒l���ƌ����܂��B���������āA���ۖ��Ƃ��ĕW�{����
�̒l���ƌ����܂��B���������āA���ۖ��Ƃ��ĕW�{����![]() ���ǂ̒��x�Ȃ�����\�Ȓl�ł��낤���Ƃ������肪�K�v�ɂȂ��Ă��܂����A���̖�����������O�ɓ��v�I���f�̊�{�I�l�����ɐG��Ă������Ƃɂ��܂��B
���ǂ̒��x�Ȃ�����\�Ȓl�ł��낤���Ƃ������肪�K�v�ɂȂ��Ă��܂����A���̖�����������O�ɓ��v�I���f�̊�{�I�l�����ɐG��Ă������Ƃɂ��܂��B
�@�����ŁA���{�×�����`��钚���q�����ɂ��ē��v�I���f���l���Ă݂邱�Ƃɂ��܂��B�T�C�R����U���Ē��������o��m���̓C�J�T�}�����Ȃ���Ή���U���Ă����̊m����![]() �ł��邱�Ƃ͌o���I�ɂ����_�I���m���Ă��܂��B�������A�T�C�R�����Q���ĐU�����Ƃ��ɂ��܂��ܒ������邢�͔����Ƒ����ē����ڂ��o��ꍇ�����R�ɂ͂��蓾�邱�Ƃ��l�����A���̊m����
�ł��邱�Ƃ͌o���I�ɂ����_�I���m���Ă��܂��B�������A�T�C�R�����Q���ĐU�����Ƃ��ɂ��܂��ܒ������邢�͔����Ƒ����ē����ڂ��o��ꍇ�����R�ɂ͂��蓾�邱�Ƃ��l�����A���̊m����![]() �ł��B���l�ɂR���ĐU�����Ƃ��ɋ��R�ɒ��������邢�͔������Əo��m����
�ł��B���l�ɂR���ĐU�����Ƃ��ɋ��R�ɒ��������邢�͔������Əo��m����![]() �ƂȂ�A��ʂ�
�ƂȂ�A��ʂ�![]() ���ăT�C�R����U�����Ƃ��ɋ��R�����肠�邢�͔�����̖ڂ��o��m����
���ăT�C�R����U�����Ƃ��ɋ��R�����肠�邢�͔�����̖ڂ��o��m����![]() �ƂȂ�܂��B
�ƂȂ�܂��B
�@���܁A�ǎ҂̓�l�i�b�Ɖ��j���^���������q��������͂߂Ɋׂ�A��l�Ƃ��Ȃ��Ȃ��̂����������̓x�ɂ������ɓq�������̂Ɖ��肵�܂��B���̓q�����搂�����̓N���[���ȃC���[�W�́u�C�J�T�}�͂��Ȃ��v�i�����j�Ƃ������̂ł����B���A�������A�����ɂ́A�ŏ���5��܂ł̏����ł�搂�����ʂ�C�J�T�}�͍s���Ȃ������̂ł����A���܂��܂��̓��͒�����̖ڂ������A6��ڈȍ~�̓T�C�R���ɍH�����Ă��������o��悤�ȃC�J�T�}�����Ă����Ƃ��܂��B���̂Ƃ��A�b�Ɖ��̂Ƃ����s�������v�I���f�̍l�����̊�{�ƂȂ�܂��B�b�͐����A���e���m�̂����������������n�߂Ă܂�2�����������Ȃ��̂ɁA���̓q���̓C�J�T�}�ł���Ɣ��f���Ȃ��R���đޏꂵ�܂����B����̓C�J�T�}�����Ă��Ȃ��Ƃ��������i�����j���������̂ɃC�J�T�}�����Ă���Ƃ�������������f���A���e�e���Ă��܂����ߌ�ierror�j�ł���A������u����̉ߌ�v�i�A���e���m�̌��A Type �T error���邢��error of the first kind�j�ƌ����܂��B����ɑ��A���͐����{���������m�̂������A�����������n�߂Ă���10������̖ڂ������ďo�Ă���̂ɁA���ł�����܂�����Ȃ��Ƃ����邾�낤�Ƃ����Ƃ��C�J�T�}�ɋC�t���Ȃ��l�q�ŁA�����������Ă�Ă�ɂȂ�܂ʼn��x������q�������Ă��܂����B������̍l�����͊m�����v�̗��_���炷���10���Ē��̖ڂ��o��m����![]() �����͂��蓾��킯�ł�����A搂�����i�����j�ʂ�C�J�T�}���S���s���Ă��Ȃ������Ȃ�A���̉��̔��f�ɂ͊ԈႢ���Ȃ������ƌ����܂����A�����ɂ�6��ڈȍ~�̒��������ł̓C�J�T�}���s���Ă��莖���͉����Ƃ͈Ⴄ�̂ɁA���̉��������܂ł��������Ɣ��f�����{���������m�̉��̔��f�ɂ͂�͂�d��ȉߌ낪��܂��B���̂悤�Ȏ����͊Ԉ���Ă���i�����͐������Ȃ��j�̂ɉ����𐳂����Ɣ��f����ߌ�̂��Ƃ��u���̉ߌ�v�i�{���������m�̌��A Type �U error���邢�� error of the second kind�j�ƌ����܂��B�����āA�b������������̔Ƃ����ߌ�̎��_�ł̊m��
�����͂��蓾��킯�ł�����A搂�����i�����j�ʂ�C�J�T�}���S���s���Ă��Ȃ������Ȃ�A���̉��̔��f�ɂ͊ԈႢ���Ȃ������ƌ����܂����A�����ɂ�6��ڈȍ~�̒��������ł̓C�J�T�}���s���Ă��莖���͉����Ƃ͈Ⴄ�̂ɁA���̉��������܂ł��������Ɣ��f�����{���������m�̉��̔��f�ɂ͂�͂�d��ȉߌ낪��܂��B���̂悤�Ȏ����͊Ԉ���Ă���i�����͐������Ȃ��j�̂ɉ����𐳂����Ɣ��f����ߌ�̂��Ƃ��u���̉ߌ�v�i�{���������m�̌��A Type �U error���邢�� error of the second kind�j�ƌ����܂��B�����āA�b������������̔Ƃ����ߌ�̎��_�ł̊m��![]() �̂��Ƃ��u�댯���v�icritical
rate�j�Ɠ��v�w�ł͌Ă�ł��܂��B���Ȃ킿�A�b�̊댯���i�b������̉ߌ��Ƃ��댯���j��
�̂��Ƃ��u�댯���v�icritical
rate�j�Ɠ��v�w�ł͌Ă�ł��܂��B���Ȃ킿�A�b�̊댯���i�b������̉ߌ��Ƃ��댯���j��![]() �ł���A���̊댯���i��������̉ߌ��Ƃ��m���j��
�ł���A���̊댯���i��������̉ߌ��Ƃ��m���j��![]() �Ƃ������Ƃł��B
�Ƃ������Ƃł��B
�@���̎����Ɣ��f�̊W��\�ɂ���Ɖ��\�̂悤�ɂȂ�܂��B�������f�������ɓ�����������̂ł����A���v�I���f�ł͂���댯���ő���̉ߌ�����̉ߌ��Ƃ��\��������܂��B�܂�A����̉ߌ������̉ߌ�������ɋN�����Ȃ��悤�Ȕ��f�͓���Ƃ������Ƃł��B���Ȃ킿�A�{���ǂ���̉ߌ���ł��邾���������Ȃ�悤�Ȕ��f���ł�������̂ł����A�����ɂ͂�����̃f�[�^���ł͑��̉ߌ������������Ƃ���ɉ����đ���̉ߌ�͑傫���Ȃ�܂��B�����ŁA���v�w�ōs����������́A����̉ߌ��Ƃ��m���i�댯���j�����߂Ĕ��f���A����̉ߌ�ɂ��Ă͕]�����s��Ȃ��̂����ʂł����A���̏ꍇ�A�f�[�^�̃o���c�L�i���U�j�����炷���ƂƂƃf�[�^�̐��𑝂₷���Ƃɂ���āA���Ȃ킿�A![]() �����������邱�Ƃɂ���āA����̉ߌ�����Ȃ����邱�Ƃ��ł��܂��B
�����������邱�Ƃɂ���āA����̉ߌ�����Ȃ����邱�Ƃ��ł��܂��B
|
���� |
�����͐������Ɣ��f���� |
�����͌��Ɣ��f���� |
|
�����͐����� |
�� |
����̉ߌ�i�A���e���m�̌��j |
|
�����͌�� |
����̉ߌ�i�{���������m�̌��j |
�� |
�@���āA���悢��{��ɖ߂邱�Ƃɂ��܂��傤�B��}�͕ꕽ�ς�![]() �ŕꕪ�U��
�ŕꕪ�U��![]() �̕�W�c����
�̕�W�c����![]() �̑傫���̔C�ӕW�{�𒊏o�����Ƃ��̕W�{����
�̑傫���̔C�ӕW�{�𒊏o�����Ƃ��̕W�{����![]() �̕��z�i���K���z
�̕��z�i���K���z![]() ��\���Ă��܂����A�W�{����
��\���Ă��܂����A�W�{����![]() �̒l���ꕽ��
�̒l���ꕽ��![]() ���痣���Η����قNj}���ɂ��̎����m��
���痣���Η����قNj}���ɂ��̎����m��![]() �͏������Ȃ�
�͏������Ȃ�![]() �ł�
�ł�![]() �ƂȂ��Ď������͑S�����蓾�Ȃ����ƂɂȂ��Ă��܂��܂��B�����ŁA
�ƂȂ��Ď������͑S�����蓾�Ȃ����ƂɂȂ��Ă��܂��܂��B�����ŁA![]() �̒l���W�{�̕��ςƂ��Ăǂ̒��x�܂ł����e�ł�����E�������߂�K�v������܂����A�킽�������͌o���I��
�̒l���W�{�̕��ςƂ��Ăǂ̒��x�܂ł����e�ł�����E�������߂�K�v������܂����A�킽�������͌o���I��![]() �ȉ��̊m�������Ȃ��l�͂߂����ɋN���肻���ɂ��Ȃ������l�ł��낤�ƍl����̂��Ó��Ƃ݂Ȃ��܂��B���Ȃ킿�A��}�ł͗���������
�ȉ��̊m�������Ȃ��l�͂߂����ɋN���肻���ɂ��Ȃ������l�ł��낤�ƍl����̂��Ó��Ƃ݂Ȃ��܂��B���Ȃ킿�A��}�ł͗���������![]() �ɂȂ�Ƃ���ł�����Б����ɂ����
�ɂȂ�Ƃ���ł�����Б����ɂ����![]() �ȉ��ɂȂ�
�ȉ��ɂȂ�![]() �������������ɂȂ��l���ƌ����܂��B���̌��E�_�̂��Ƃ�M�����E�ƌĂсA��}�ł͐M�������
�������������ɂȂ��l���ƌ����܂��B���̌��E�_�̂��Ƃ�M�����E�ƌĂсA��}�ł͐M�������![]() �ł���M��������
�ł���M��������![]() �ƂȂ�܂��B1.96�Ƃ��������͐��K���z�̃p�[�Z���g�_�̕\��0.025�ɑ�������l�ł��B���Ȃ킿�A�W�{����
�ƂȂ�܂��B1.96�Ƃ��������͐��K���z�̃p�[�Z���g�_�̕\��0.025�ɑ�������l�ł��B���Ȃ킿�A�W�{����![]() ��95%�M����ԁiconfidence interval�j��
��95%�M����ԁiconfidence interval�j��
![]()
���邢��
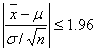
�ƂȂ�܂��B���������āA��}�̕W�{����![]() �͂��̋�ԓ��ɓ����Ă��邩��̑��\�ȕW�{���ςł���A�W�{����
�͂��̋�ԓ��ɓ����Ă��邩��̑��\�ȕW�{���ςł���A�W�{����![]() �͂��̋�ԊO�ɂ��邩����p���ׂ��W�{���ςł���ƌ����܂��B�������A���̂悤�Ȕ��f�������Ƃ��ɑ���̉ߌ��Ƃ��댯����5%�ł���Ƃ������ƂɂȂ�܂��B
�͂��̋�ԊO�ɂ��邩����p���ׂ��W�{���ςł���ƌ����܂��B�������A���̂悤�Ȕ��f�������Ƃ��ɑ���̉ߌ��Ƃ��댯����5%�ł���Ƃ������ƂɂȂ�܂��B
�@���̂悤�ȐM����Ԃɂ��Ă̊W����ό`�����
![]()
�Ƃ����W���������܂����A����͕W�{����![]() ����95%�̐M�����ŕꕽ��
����95%�̐M�����ŕꕽ��![]() �̐M����Ԃ𐄒肷�邱�Ƃ��ł���Ƃ������ƂƓ����ɂȂ�܂��B
�̐M����Ԃ𐄒肷�邱�Ƃ��ł���Ƃ������ƂƓ����ɂȂ�܂��B
�@�����ŁA�ϐ�![]() ���K���ϐ�
���K���ϐ�![]() �ŕϊ������
�ŕϊ������
![]()
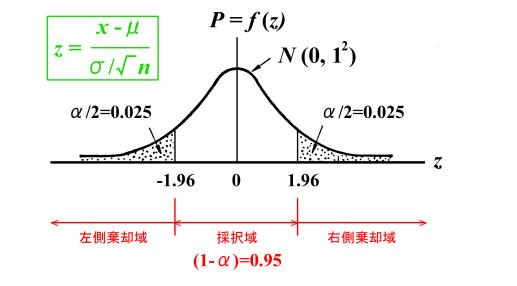
�̂悤�ɂȂ邪�A���̕ϐ�![]() ���܂����}�̂悤�ȕW�����K���z
���܂����}�̂悤�ȕW�����K���z![]() ������̂ŁA���̐}�ŐM����Ԃ����߂�����킩��₷�������m��܂���B
������̂ŁA���̐}�ŐM����Ԃ����߂�����킩��₷�������m��܂���B
�@���Ȃ݂ɁA���p��irejection
region�j�ɑ�������m��![]() �̂��Ƃ��u�댯���v�icritical
rate�j�ƌ������A���f�̊�ƂȂ�m���Ƃ����Ӗ��Łu�L�Ӑ����v�isignificance level���邢��level of significance�j�ƌĂԂ��Ƃ�����܂��B�܂��A����Ƃ͋t�ɍ̑���iacceptance region�j��
�̂��Ƃ��u�댯���v�icritical
rate�j�ƌ������A���f�̊�ƂȂ�m���Ƃ����Ӗ��Łu�L�Ӑ����v�isignificance level���邢��level of significance�j�ƌĂԂ��Ƃ�����܂��B�܂��A����Ƃ͋t�ɍ̑���iacceptance region�j��![]() �ɑ�������m���ł���A���̊m���̂��Ƃ�
�ɑ�������m���ł���A���̊m���̂��Ƃ�![]() �M�������邢�͐M���W���iconfidence
coefficient�j�ƌĂ�ł��܂��B����ł́A�L�Ӑ�����5%�Ƃ����̂͂ǂ��������Ƃ��Ӗ����Ă��邩�Ƃ����ƁA�����Ƃ��Ċ��p���邱�Ƃ�\�����ė��Ă������i���̂悤�ȉ����̂��Ƃ��A�������inull hypothesis�j�ƌ����A�ʏ�
�M�������邢�͐M���W���iconfidence
coefficient�j�ƌĂ�ł��܂��B����ł́A�L�Ӑ�����5%�Ƃ����̂͂ǂ��������Ƃ��Ӗ����Ă��邩�Ƃ����ƁA�����Ƃ��Ċ��p���邱�Ƃ�\�����ė��Ă������i���̂悤�ȉ����̂��Ƃ��A�������inull hypothesis�j�ƌ����A�ʏ�![]() �Ƃ����L�����g���܂��j�����p�����Ƃ��Ă��A���̂��Ƃɂ�����5%�ȉ��ł���Ƃ������Ƃł��B����������A�{���͋A�������������������ɂ�������炸�A��������p���邱�Ƃɂ���Č��i����̉ߌ�j��Ƃ������m��Ȃ��댯��100��̂����T��܂ł͔F�߂Ă������Ƃ������ƂƓ����ł��̂ŁA�L�Ӑ���
�Ƃ����L�����g���܂��j�����p�����Ƃ��Ă��A���̂��Ƃɂ�����5%�ȉ��ł���Ƃ������Ƃł��B����������A�{���͋A�������������������ɂ�������炸�A��������p���邱�Ƃɂ���Č��i����̉ߌ�j��Ƃ������m��Ȃ��댯��100��̂����T��܂ł͔F�߂Ă������Ƃ������ƂƓ����ł��̂ŁA�L�Ӑ���![]() �̂��Ƃ��댯���ƌ����ꍇ�������̂ł��B�A�������i���Ƃ��A
�̂��Ƃ��댯���ƌ����ꍇ�������̂ł��B�A�������i���Ƃ��A![]() �j�ɑ��A
�j�ɑ��A![]() �ƂȂ�悤�ȉ����̂��Ƃ�Η������ialternative hypothesis�j�ƌĂ�
�ƂȂ�悤�ȉ����̂��Ƃ�Η������ialternative hypothesis�j�ƌĂ�![]() �Ƃ����L����p���܂��B���R�A�A�����������p����ꍇ�͑Η��������̗p���邱�ƂɂȂ�܂��B
�Ƃ����L����p���܂��B���R�A�A�����������p����ꍇ�͑Η��������̗p���邱�ƂɂȂ�܂��B
�@���̂悤�ɁA���v�I��������ɂ����ẮA�A������![]() ���������ɂ�������炸��������p���Ă��܂���肪����̉ߌ�ł���A��ʂɂ��̌��̊m����
���������ɂ�������炸��������p���Ă��܂���肪����̉ߌ�ł���A��ʂɂ��̌��̊m����![]() �Ƃ����L���ŕ\���A����
�Ƃ����L���ŕ\���A����![]() �̂��Ƃ��댯���ƌĂ�L�Ӑ����ƌĂ肵�܂��B�܂��A���̊m��
�̂��Ƃ��댯���ƌĂ�L�Ӑ����ƌĂ肵�܂��B�܂��A���̊m��![]() �ɑ�������K���ϐ�
�ɑ�������K���ϐ�![]() ��̓_
��̓_![]() �̂��Ƃ�L�Ӑ����_�ƌĂ�ł��܂��B���������āA�댯����L�Ӑ����Ƃ����̂͑���̉ߌ��Ƃ��m���ł���ƊȌ��Ɍ������Ƃ��ł��܂��B����ɑ��A�Η��������������i�A�������͌��j�̂ɂ�������o�ł��Ȃ��̂�����̉ߌ�ŁA���̊m�����L��
�̂��Ƃ�L�Ӑ����_�ƌĂ�ł��܂��B���������āA�댯����L�Ӑ����Ƃ����̂͑���̉ߌ��Ƃ��m���ł���ƊȌ��Ɍ������Ƃ��ł��܂��B����ɑ��A�Η��������������i�A�������͌��j�̂ɂ�������o�ł��Ȃ��̂�����̉ߌ�ŁA���̊m�����L��![]() ���g���ĕ\���̂���ʓI�ł��B�܂��A
���g���ĕ\���̂���ʓI�ł��B�܂��A![]() �ɑ�������m���̂��Ƃ��u���o�́v�ƌĂ�ł��܂��B
�ɑ�������m���̂��Ƃ��u���o�́v�ƌĂ�ł��܂��B
�@���v�I��������ɂ�����댯���i�L�Ӑ����j![]() �A�M����
�A�M����![]() �A����̉ߌ��Ƃ��m��
�A����̉ߌ��Ƃ��m��![]() �A����ь��o��
�A����ь��o��![]() �̊W�͉��}�Ɏ����Ă���܂��B
�̊W�͉��}�Ɏ����Ă���܂��B
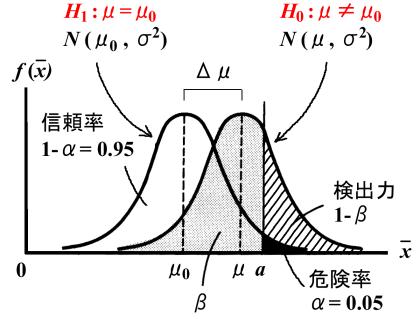
�@���܁A�����W�c�̕ꕽ��![]() ��
��![]() �ɓ������Ƃ����A������
�ɓ������Ƃ����A������![]() �𗧂āA�Η������Ƃ���
�𗧂āA�Η������Ƃ���![]() �i���Ȃ킿�A�^�̕ꕽ��
�i���Ȃ킿�A�^�̕ꕽ��![]() �͋A�������ʼn��肵���l
�͋A�������ʼn��肵���l![]() ���
���![]() �����傫���j��M����
�����傫���j��M����![]() �ő傫��
�ő傫��![]() �̔C�ӕW�{�ɂ��ĉ������肵�Ă݂邱�Ƃɂ��܂��B���̏ꍇ�A�Η�������
�̔C�ӕW�{�ɂ��ĉ������肵�Ă݂邱�Ƃɂ��܂��B���̏ꍇ�A�Η�������![]() �Ȃ̂ʼnE�Б���������邱�ƂɂȂ�܂��B���������āA�댯��
�Ȃ̂ʼnE�Б���������邱�ƂɂȂ�܂��B���������āA�댯��![]() �ɑ�������L�Ӑ����_�͐��K���z
�ɑ�������L�Ӑ����_�͐��K���z![]() �Ȑ����
�Ȑ����![]() �ɂȂ�A����
�ɂȂ�A����![]() �_���E���̍����������A������
�_���E���̍����������A������![]() �̊��p��ɂȂ�A�Η�����
�̊��p��ɂȂ�A�Η�����![]() ���̑����邱�ƂɂȂ�܂��B�܂��A����
���̑����邱�ƂɂȂ�܂��B�܂��A����![]() �_��荶���̕����͂��ׂċA������
�_��荶���̕����͂��ׂċA������![]() �����p�ł����A�A������
�����p�ł����A�A������![]() ���̑����邱�ƂɂȂ�܂��B�������Ȃ���A��}�Ō���悤�ɁA�Η������ł���
���̑����邱�ƂɂȂ�܂��B�������Ȃ���A��}�Ō���悤�ɁA�Η������ł���![]() ���^���ł������Ƃ���ƁA���K���z
���^���ł������Ƃ���ƁA���K���z![]() �Ȑ����
�Ȑ����![]() �_��荶���̕����i�e�̕����j�̕W�{����
�_��荶���̕����i�e�̕����j�̕W�{����![]() �͐��K���z
�͐��K���z![]() �Ȑ��̋A������
�Ȑ��̋A������![]() �̑���ɓ����Ă��܂��A�A������
�̑���ɓ����Ă��܂��A�A������![]() ���������Ȃ��i�Η�����
���������Ȃ��i�Η�����![]() ���������j�̂ɋA������
���������j�̂ɋA������![]() ���������Ƃ����Ԉ�������f�i����̉ߌ�j�����Ă��܂����ƂɂȂ�܂��B���Ȃ킿�A���K���z
���������Ƃ����Ԉ�������f�i����̉ߌ�j�����Ă��܂����ƂɂȂ�܂��B���Ȃ킿�A���K���z![]() �Ȑ���̉e�̕���������̉ߌ��Ƃ��m��
�Ȑ���̉e�̕���������̉ߌ��Ƃ��m��![]() �ɑ�������킯�ł��B�����āA���K���z
�ɑ�������킯�ł��B�����āA���K���z![]() �Ȑ���̎ΐ����������o��
�Ȑ���̎ΐ����������o��![]() �ɂȂ�܂��B���o��
�ɂȂ�܂��B���o��![]() ���グ��Α��ΓI�ɑ���̉ߌ��Ƃ��m��
���グ��Α��ΓI�ɑ���̉ߌ��Ƃ��m��![]() �������邱�Ƃ��ł���̂ŁA���Ɍ��o��
�������邱�Ƃ��ł���̂ŁA���Ɍ��o��![]() �����߂�ɂ͂ǂ�������悢�����l���܂��B
�����߂�ɂ͂ǂ�������悢�����l���܂��B
�@���K���z![]() �̌��o��
�̌��o��![]() �ɑΉ����鐳�K���z
�ɑΉ����鐳�K���z![]() �̗L�Ӑ����_
�̗L�Ӑ����_![]() �͐��K���z
�͐��K���z![]() �̉E�Б������
�̉E�Б������![]() �_�ł��邩��
�_�ł��邩��
![]()
�ƂȂ�܂��B����A����![]() �_�͐��K���z
�_�͐��K���z![]() �Ȑ���ɂ��邩��A���̊m��
�Ȑ���ɂ��邩��A���̊m��![]() �̎n�_�ɑ�������K���ϐ��̒l��
�̎n�_�ɑ�������K���ϐ��̒l��![]() �Ƃ����
�Ƃ����
![]()
�ƂȂ�̂ŁA![]() �̊W���l������
�̊W���l������![]() �����߂��
�����߂��
![]()
![]()
�ƂȂ�܂��B
�����ŁA���K���z![]() �̕W�{����
�̕W�{����![]() ���K���ϐ�
���K���ϐ�![]() �ɕϊ�����
�ɕϊ�����
![]()
�Ƃ���A���o��![]() �͐��K���z
�͐��K���z![]() �̋K���ϐ�
�̋K���ϐ�![]() �����K���z
�����K���z![]() �̊��p��ɗ�����m���A���Ȃ킿�A
�̊��p��ɗ�����m���A���Ȃ킿�A![]() ������
������
![]()
�ƂȂ�܂��B���o��![]() �����߂邽�߂ɂ͊m��
�����߂邽�߂ɂ͊m��![]() ��傫������悢�̂ŁA
��傫������悢�̂ŁA![]() ���̏������ł�
���̏������ł�
![]()
�Ƃ������������A���o��![]() �����܂�A���ΓI�ɑ���̉ߌ��Ƃ��m��
�����܂�A���ΓI�ɑ���̉ߌ��Ƃ��m��![]() ���������ł��邱�Ƃ��킩��܂��B
���������ł��邱�Ƃ��킩��܂��B
�@��q�̓��v�I��������͕Б�����̏ꍇ��z�肵�čs�������A��������̏ꍇ���l�����Ă����K�v������ł��傤�B��������̏ꍇ�́A�����W�c�̕ꕽ��![]() ��
��![]() �ɓ������Ƃ����A������
�ɓ������Ƃ����A������![]() �𗧂āA�Η������Ƃ���
�𗧂āA�Η������Ƃ���![]() �i���Ȃ킿�A�^�̕ꕽ��
�i���Ȃ킿�A�^�̕ꕽ��![]() �͋A�������ʼn��肵���l
�͋A�������ʼn��肵���l![]() �Ƃ͈���Ă���j��M����
�Ƃ͈���Ă���j��M����![]() �ő傫��
�ő傫��![]() �̔C�ӕW�{�ɂ��ĉ������肷�邱�ƂɂȂ�܂��B���̏ꍇ�A�Η�������
�̔C�ӕW�{�ɂ��ĉ������肷�邱�ƂɂȂ�܂��B���̏ꍇ�A�Η�������![]() �Ȃ̂ŗ�����������邱�ƂɂȂ�܂��B���������āA�댯��
�Ȃ̂ŗ�����������邱�ƂɂȂ�܂��B���������āA�댯��![]() �ɑ�������L�Ӑ����_�́A���}�̐��K���z
�ɑ�������L�Ӑ����_�́A���}�̐��K���z![]() �Ȑ����
�Ȑ����![]() ��
��![]() �ɂȂ�A����
�ɂȂ�A����![]() �_���E���̍������������
�_���E���̍������������![]() �_��荶���̍����������A������
�_��荶���̍����������A������![]() �̊��p��ɂȂ�A�Η�����
�̊��p��ɂȂ�A�Η�����![]() ���̑����邱�ƂɂȂ�܂��B�܂��A����
���̑����邱�ƂɂȂ�܂��B�܂��A����![]() �_��
�_��![]() �_�ɂ͂��܂ꂽ�����͂��ׂċA������
�_�ɂ͂��܂ꂽ�����͂��ׂċA������![]() �����p�ł����A�A������
�����p�ł����A�A������![]() ���̑����邱�ƂɂȂ�܂��B
���̑����邱�ƂɂȂ�܂��B
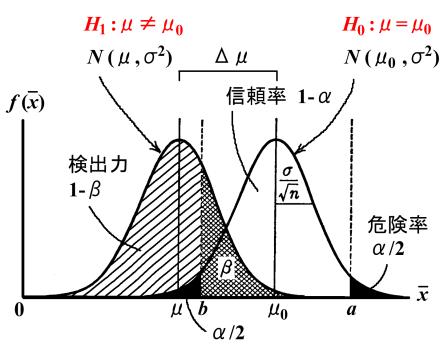
�@�������Ȃ���A��}�Ō���悤�ɁA�Η������ł���![]() �i�ƂƂ��ΐ^�̕ꕽ��
�i�ƂƂ��ΐ^�̕ꕽ��![]() �͋A�������̒l
�͋A�������̒l![]() ���
���![]() ��������Ă���j���^���ł������Ƃ���ƁA���K���z
��������Ă���j���^���ł������Ƃ���ƁA���K���z![]() �̕ꕽ��
�̕ꕽ��![]() �����炩�ɐ��K���z
�����炩�ɐ��K���z![]() �̊��p��ɓ����Ă���i���������āA
�̊��p��ɓ����Ă���i���������āA![]() ���������j�ɂ�������炸�A���K���z
���������j�ɂ�������炸�A���K���z![]() �Ȑ����
�Ȑ����![]() �_���E���̕����i�e�̕����j�̕W�{����
�_���E���̕����i�e�̕����j�̕W�{����![]() �͐��K���z
�͐��K���z![]() �Ȑ��̋A������
�Ȑ��̋A������![]() �̑���ɓ����Ă��܂��A�A������
�̑���ɓ����Ă��܂��A�A������![]() ���������Ȃ��i�Η�����
���������Ȃ��i�Η�����![]() ���������j�̂ɋA������
���������j�̂ɋA������![]() ���������Ƃ����Ԉ�������f�i����̉ߌ�j�����Ă��܂����ƂɂȂ�܂��B���Ȃ킿�A���K���z
���������Ƃ����Ԉ�������f�i����̉ߌ�j�����Ă��܂����ƂɂȂ�܂��B���Ȃ킿�A���K���z![]() �Ȑ���̉e�̕���������̉ߌ��Ƃ��m��
�Ȑ���̉e�̕���������̉ߌ��Ƃ��m��![]() �ɑ�������킯�ł��B�����āA���K���z
�ɑ�������킯�ł��B�����āA���K���z![]() �Ȑ���̎ΐ����������o��
�Ȑ���̎ΐ����������o��![]() �ɂȂ�܂��B���o��
�ɂȂ�܂��B���o��![]() ���グ��Α��ΓI�ɑ���̉ߌ��Ƃ��m��
���グ��Α��ΓI�ɑ���̉ߌ��Ƃ��m��![]() �������邱�Ƃ��ł��܂��B
�������邱�Ƃ��ł��܂��B
�@�Б�����̏ꍇ�Ɠ����悤�ɁA��������̏ꍇ�ɂ��Ă����o��![]() �����߂Ă݂邱�Ƃɂ��܂��B���K���z
�����߂Ă݂邱�Ƃɂ��܂��B���K���z![]() �̌��o��
�̌��o��![]() �ɑΉ����鐳�K���z
�ɑΉ����鐳�K���z![]() �̗L�Ӑ����_
�̗L�Ӑ����_![]() ��
��![]() �͂��ꂼ�ꐳ�K���z
�͂��ꂼ�ꐳ�K���z![]() �̗��������
�̗��������![]() �_�ł��邩��
�_�ł��邩��
![]()
�ƂȂ�܂��B����A����![]() �_��
�_��![]() �_�͂���������K���z
�_�͂���������K���z![]() �Ȑ���ɂ��邩��A���̊m��
�Ȑ���ɂ��邩��A���̊m��![]() �̎n�_�ɑ�������K���ϐ��̒l��
�̎n�_�ɑ�������K���ϐ��̒l��![]() �����
�����![]() �Ƃ����
�Ƃ����
![]()
�ƂȂ�̂ŁA![]() �̊W���l������
�̊W���l������![]() ��
��![]() �����߂��
�����߂��
![]()
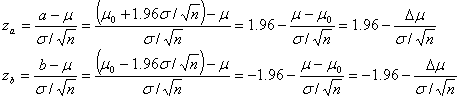
�ƂȂ�܂��B
�����ŁA���K���z![]() �̕W�{����
�̕W�{����![]() ���K���ϐ�
���K���ϐ�![]() �ɕϊ�����
�ɕϊ�����
![]()
�Ƃ���A���o��![]() �͐��K���z
�͐��K���z![]() �̋K���ϐ�
�̋K���ϐ�![]() �����K���z
�����K���z![]() �̊��p��ɗ�����m���A���Ȃ킿�A�m��
�̊��p��ɗ�����m���A���Ȃ킿�A�m��![]() ����ъm��
����ъm��![]() �̑��a������
�̑��a������
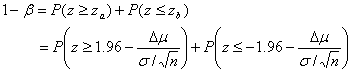
�ƂȂ�܂��B
�@�W�{�̑傫��![]() �ɂ���Č��o��
�ɂ���Č��o��![]() ���ǂ̂悤�ɕς��̂����댯��
���ǂ̂悤�ɕς��̂����댯��![]() �̗�������̏�������
�̗�������̏�������![]() �����ɂ��ăv���b�g�������̂����}�Ɏ����܂��B���o�͋Ȑ��̋t��OP�Ȑ��i�I�y���[�V�����Ȑ��j�ł��BOP�Ȑ���
�����ɂ��ăv���b�g�������̂����}�Ɏ����܂��B���o�͋Ȑ��̋t��OP�Ȑ��i�I�y���[�V�����Ȑ��j�ł��BOP�Ȑ���![]() �����v�p�����[�^�[�ɂ���Ăǂ��ς�邩���v���b�g�������̂ŁA������茟���Ɏg�p����܂��B
�����v�p�����[�^�[�ɂ���Ăǂ��ς�邩���v���b�g�������̂ŁA������茟���Ɏg�p����܂��B
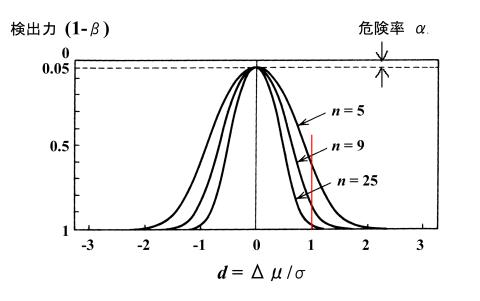
�@���Ƃ��A�ꕽ�ς̍����ꕪ�U���x�i![]() �j�ł���ꍇ�͌��o�͋Ȑ��ƐԐ��̌�_�̓ǂ݂���A�W�{�̑傫����
�j�ł���ꍇ�͌��o�͋Ȑ��ƐԐ��̌�_�̓ǂ݂���A�W�{�̑傫����![]() �̂Ƃ��͌��o��
�̂Ƃ��͌��o��![]() �͖�60%�A
�͖�60%�A![]() �̂Ƃ��͖�85%�A
�̂Ƃ��͖�85%�A![]() �̂Ƃ��͂قƂ��100%�߂��ɂȂ邱�Ƃ��킩��܂��B�܂��A�ꕽ�ς̍����ꕪ�U��2�{�ȏ�i
�̂Ƃ��͂قƂ��100%�߂��ɂȂ邱�Ƃ��킩��܂��B�܂��A�ꕽ�ς̍����ꕪ�U��2�{�ȏ�i![]() �j�ł���ꍇ�́A�W�{�̑傫����
�j�ł���ꍇ�́A�W�{�̑傫����![]() �ł����Ă����o��
�ł����Ă����o��![]() �͂ق�100%�ɂȂ�A����̉ߌ��Ƃ��\���͂قƂ�ǂȂ��i
�͂ق�100%�ɂȂ�A����̉ߌ��Ƃ��\���͂قƂ�ǂȂ��i![]() �j���Ƃ��킩��܂��B
�j���Ƃ��킩��܂��B
�i���j��W�c�͐��K���z�ł���A�ꕪ�U![]() �͊��m�ł���Ƃ��܂��B���̂Ƃ�
�͊��m�ł���Ƃ��܂��B���̂Ƃ�
![]()
�Ƃ��������̉��ŁA�L�Ӑ���5%�ʼn���������s���A�W�{�̑傫��![]() �ɂ��Č��o��
�ɂ��Č��o��![]() ���v�Z���Ă݂܂��傤�B�������A�ꕽ��
���v�Z���Ă݂܂��傤�B�������A�ꕽ��![]() �̍��͕ꕪ�U
�̍��͕ꕪ�U![]() ���x�ł������Ɖ��肵�܂��B
���x�ł������Ɖ��肵�܂��B
�i�j����![]() �����
�����![]() �̗L�Ӑ���5%�̊��p��́A��������ł���̂�
�̗L�Ӑ���5%�̊��p��́A��������ł���̂�
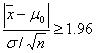
�ƂȂ�܂��B�^�̕ꕽ�ς�![]() �ł���Ƃ��A�W�{����
�ł���Ƃ��A�W�{����![]() �����̊��p��ɗ�����m�����Ȃ킿���o��
�����̊��p��ɗ�����m�����Ȃ킿���o��![]() ��
��

�ƂȂ邪�A������
![]()
�Ƃ����A���̋K���ϐ�![]() �͕W�����K���z
�͕W�����K���z![]() �ɏ]���܂��B�����
�ɏ]���܂��B�����
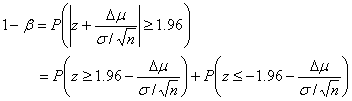
�ƂȂ�܂��B��ӂ��
![]()
������A���߂錟�o��![]() ��
��
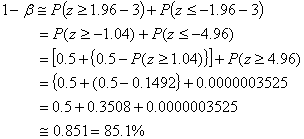
�ƂȂ�܂��B