χ2(カイ2乗)分布
いま赤い玉と白い玉が同数ずつたくさん入った箱をよくかき混ぜてから目隠しをして20個の玉を取ったとします。目隠しをはずし取り出した玉の数を数えたところ、赤玉が12個、白玉が8個でした。確率の教えるところによれば、箱の中の玉の種類は同数だから、ランダムに取り出される玉の種類の数は同数、すなわち、赤玉10個、白玉10個になるはずで、これが確率論的期待値です。
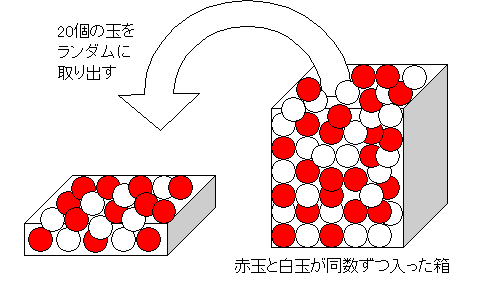
しかしながら、現実に取り出された玉の数(実現値)はこの期待値とずれています。そこで、このような理想と現実のずれを測る尺度として、次のような「食い違いの測度」を定義することにします。
![]()
この例では箱の中の玉は赤と白の2種類だからn=2になり、実現値1は赤玉の12、実現値2は白玉の8で、期待値1は赤玉の10、期待値2は白玉の10です。したがって、食い違いの測度は今回の実験では
![]()
となります。同じような実験をまた繰り返したところ、今度は赤玉が9個、白玉が11個になりました。したがって
![]()
となります。さらに、実験を繰り返したところ、今度は赤玉と白玉の数が期待値と同じ10個ずつになりました。この時の食い違いの測度を計算してみると
![]()
のように食い違いの測度が0になり、確かに食い違いがないことがわかります。
さらに、めったに起こりそうにない例(赤玉20個と白玉0個、あるいはその逆)について、食い違いの測度を計算してみると
![]()
となり、起こりそうもない事象が起きる場合には食い違いの測度は0よりだんだん大きくなるが、この場合は20を超えることはありません。しかしながら、玉を箱からもっとたくさん取り出すような場合には食い違いの測度の上限はさらに大きくなり、極限では∞までの値を取り得ます。
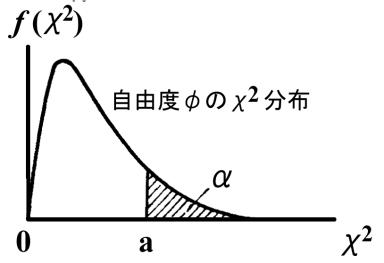
このような赤玉と白玉を箱からランダムに取り出す実験を無限回繰り返し、その食い違いの測度を横軸に、またその測度に相当する事象が起きた回数(度数)の相対値(確率密度)を縦軸にプロットすると、次図のような曲線が得られます。

この曲線のことをχ2(カイ2乗)分布曲線と言い、期待値からのずれの度合いを判定するのに用いられます。上図で赤く示した範囲は対象となるある事象の出現確率が5%以下である範囲を示し、χ2=3.841以上の食い違いの測度が観測されたときは5%以下というめったに起こらない事象が何らかの理由で起こったと言うことになります。
玉の種類がもう一種増えた場合についてもχ2分布曲線を描くことができますが、その時の自由度φは、玉の種類がn=3ですから、φ=n−1=3−1=2となり、またχ2の5%境界値は5.991となります。当然のことですが自由度2のχ2分布曲線は上図の自由度1のχ2分布曲線とは形が異なります。もちろん、自由度がさらに増えたχ2分布曲線も描くことができます。
先ほどの例では赤玉と白玉の数は同数でしたが、箱の中の玉の種類の数の割合が異なっていても、また取り出す玉の数が違っていても、自由度が1である限り上図と同じχ2分布曲線となりますから、χ2分布曲線は確率統計学の上で汎用性のある重要な曲線となっています。
自由度φのχ2分布の確率密度関数は理論的にはΓ(ガンマ)関数
![]()
を使った次式で表されます。
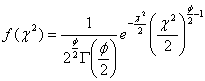
Γ(ガンマ)関数には次のような性質があります。
1)![]()
2)![]()
3)![]()
4)![]()
5)![]()
この確率密度関数![]() を
を![]() に対してプロットしたものが前掲した
に対してプロットしたものが前掲した![]() 分布曲線(
分布曲線(![]() の場合)です。また、自由度
の場合)です。また、自由度![]() が1から10まで変化した場合の
が1から10まで変化した場合の![]() 分布曲線は下図のようになり、自由度
分布曲線は下図のようになり、自由度![]() が大きくなると
が大きくなると![]() 分布は正規分布に近づきます。
分布は正規分布に近づきます。

![]() がある値
がある値![]() より大きくなる確率
より大きくなる確率![]() は、理論的に次式で与えられます。
は、理論的に次式で与えられます。

![]() 分布が統計学上重要な分布であることは、正規母集団(母平均μ、母分散σ2)の確率密度関数
分布が統計学上重要な分布であることは、正規母集団(母平均μ、母分散σ2)の確率密度関数![]() と比べて見るとよくわかります。すなわち、正規分布については
と比べて見るとよくわかります。すなわち、正規分布については![]() は
は
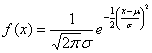
のような確率密度関数になっており、![]() の
の![]() 分布の確率密度関数
分布の確率密度関数
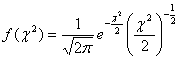
において、![]() とおけば、両関数の骨格はほとんど一致することが理解できると思います。
とおけば、両関数の骨格はほとんど一致することが理解できると思います。
また、![]() 分布については次のような重要な性質が知られています。
分布については次のような重要な性質が知られています。
1)![]() 分布の期待値と分散および標準偏差は次式で与えられます。
分布の期待値と分散および標準偏差は次式で与えられます。
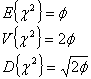
2)![]() 分布には加成性がある、すなわち、一般に
分布には加成性がある、すなわち、一般に![]() がそれぞれ自由度
がそれぞれ自由度![]() の互いに独立な
の互いに独立な![]() 分布に従うときは
分布に従うときは
![]()
は自由度![]() の
の![]() 分布に従います。
分布に従います。
上記の性質を一般の正規分布N(μ,σ2)に拡張することができます。すなわち、いま![]() がそれぞれ独立な正規分布N(μ,σ2)に従うとすれば、
がそれぞれ独立な正規分布N(μ,σ2)に従うとすれば、
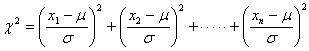
は自由度![]() の
の![]() 分布に従います。
分布に従います。
上式の右辺の各項は、確率変数![]() を母平均
を母平均![]() と母標準偏差
と母標準偏差![]() で規格化した、いわゆるz−スコア
で規格化した、いわゆるz−スコア
![]()
を2乗したものであるから、![]() 上式は
上式は
![]()
と簡略化され、![]() は標準正規分布
は標準正規分布![]() の母集団からランダムに抽出した大きさ
の母集団からランダムに抽出した大きさ![]() の標本の規格化確率変数
の標本の規格化確率変数![]() の平方和と表現することもできます。
の平方和と表現することもできます。
![]()
一方、上式でμを![]() で置き換えた場合も
で置き換えた場合も![]() 分布に従います。すなわち正規母集団
分布に従います。すなわち正規母集団![]() からランダムサンプリングした
からランダムサンプリングした![]() 個のデータの平方和(偏差2乗和)
個のデータの平方和(偏差2乗和)![]() を母分散(
を母分散(![]() )で割ったものは、自由度
)で割ったものは、自由度![]() の
の![]() 分布に従います。したがって
分布に従います。したがって
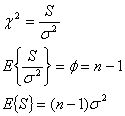
となります。
不偏分散(![]() )の定義式を考慮すれば、正規母集団
)の定義式を考慮すれば、正規母集団![]() からランダムサンプリングした
からランダムサンプリングした![]() 個のデータから求めた不偏分散
個のデータから求めた不偏分散![]() を
を![]() 倍したものは、自由度
倍したものは、自由度![]() の
の![]() 分布に従います。すなわち、
分布に従います。すなわち、
![]()
となります。
このように、![]() 分布は平方和
分布は平方和![]() や不偏分散
や不偏分散![]() と密接な関係があるため、母分散の推定や検定に利用されます。
と密接な関係があるため、母分散の推定や検定に利用されます。
3)自由度![]() の
の![]() 分布に従う
分布に従う![]() 個の確率変数からなる
個の確率変数からなる![]() に関して、
に関して、![]() の時は
の時は
![]()
![]()
が近似的に標準正規分布![]() に従うことが知られており、Fisherの近似式と呼ばれています。
に従うことが知られており、Fisherの近似式と呼ばれています。
この近似式を利用すれば、![]() 分布のパーセント点(危険率
分布のパーセント点(危険率![]() における有意水準点
における有意水準点![]() )を与える表には、その値が通常自由度
)を与える表には、その値が通常自由度![]() が100までしか与えられていないが、自由度
が100までしか与えられていないが、自由度![]() の場合は、標準正規分布表から必要とする危険率
の場合は、標準正規分布表から必要とする危険率![]() に対応する有意水準点
に対応する有意水準点![]() を読みとり、上式を変形した次式
を読みとり、上式を変形した次式
![]()
に、その有意水準点![]() の値と自由度
の値と自由度![]() を代入することにより、危険率
を代入することにより、危険率![]() における自由度
における自由度![]() の有意水準点
の有意水準点![]() を求めることが可能となります。
を求めることが可能となります。
(例題1)ここで、![]() 分布を利用した統計推理をしてみることにします。いまあるコーヒー喫茶店にコーヒーを飲みにやって来るお客さんの人数は1日に平均16人であることがわかっている場合、32人以上のお客さんがこの店にやって来る日数は1ヶ月のうちに何日あるかを推定してみて下さい。また、1日に8人以下しかお客さんが来ない日数は1ヶ月のうち何日あるでしょうか。
分布を利用した統計推理をしてみることにします。いまあるコーヒー喫茶店にコーヒーを飲みにやって来るお客さんの人数は1日に平均16人であることがわかっている場合、32人以上のお客さんがこの店にやって来る日数は1ヶ月のうちに何日あるかを推定してみて下さい。また、1日に8人以下しかお客さんが来ない日数は1ヶ月のうち何日あるでしょうか。
(解答)![]() 分布の平均は自由度
分布の平均は自由度![]() に等しいから、この場合
に等しいから、この場合![]() となります。そこで
となります。そこで
![]()
となるような危険率![]() を
を![]() 分布のパーセント点を与える表から求めると、
分布のパーセント点を与える表から求めると、![]() であることがわかります。したがって、1日に32人以上のお客さんがやって来る日数は30日×0.10=3日となります。
であることがわかります。したがって、1日に32人以上のお客さんがやって来る日数は30日×0.10=3日となります。

すなわち、1日に32人以上もコーヒーを飲みに来てくれるような盛況な日は1ヶ月に高々3日程度であることが![]() 分布から容易に推定されることになります。また、
分布から容易に推定されることになります。また、
![]()
となるような確率![]() を
を![]() 分布のパーセント点を与える表から求めると、
分布のパーセント点を与える表から求めると、![]() であることがわかります。したがって、一日に8人以下しかお客さんが来ない日数は30日×(1−0.95)=30日×0.05=1.5日と算出され、そのような日は1ヶ月に高々1日しかないことがわかります。
であることがわかります。したがって、一日に8人以下しかお客さんが来ない日数は30日×(1−0.95)=30日×0.05=1.5日と算出され、そのような日は1ヶ月に高々1日しかないことがわかります。
(例題2)ある高校で英語の試験を受けた生徒の中からランダムに10人を選び、その点数を調べたところ、次のようであった。この標本データを基に母分散の95%の信頼限界を求めて下さい。また、母分散の点推定も併せて行って下さい。
18 38 50 57 69 19 39 52 59 74
(解答)母分散![]() の正規母集団からの
の正規母集団からの![]() 個の無作為標本による
個の無作為標本による
![]()
は自由度![]() の
の![]() 分布をすることはすでに明らかです。
分布をすることはすでに明らかです。
いま危険率を![]() とすれば、下図の左側と右側の確率はそれぞれ
とすれば、下図の左側と右側の確率はそれぞれ![]() となりますが、それら確率を与える
となりますが、それら確率を与える![]() 値をそれぞれ
値をそれぞれ![]() とおきますと
とおきますと
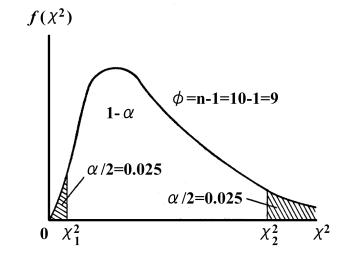
上式の![]() 値が次式の範囲に入る確率は
値が次式の範囲に入る確率は![]() となります。
となります。
![]()
変形すると
![]()
となり、この式から信頼率![]() で母分散
で母分散![]() の区間推定を行うことができます。
の区間推定を行うことができます。
そこで、問題の標本データについては、自由度![]() であるから、両側確率5%の
であるから、両側確率5%の![]() の限界値を
の限界値を![]() 分布のパーセント点を与える表から求めると、片側2.5%ずつとることになるので
分布のパーセント点を与える表から求めると、片側2.5%ずつとることになるので
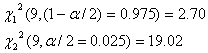
となります。
また、標本データの偏差平方和は
![]()
となるので、これらの値を下式
![]()
に代入すると、
![]()
となり、母分散![]() の95%信頼限界が求められました。
の95%信頼限界が求められました。
また、母分散![]() の点推定は不偏分散
の点推定は不偏分散![]() であるから、
であるから、
![]()
の関係式から、
![]()
のように母分散![]() の点推定値
の点推定値![]() が求められます。
が求められます。