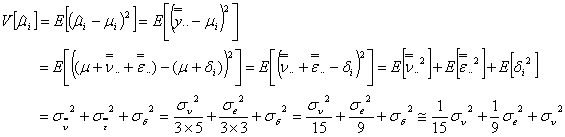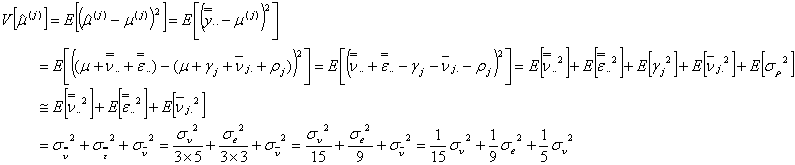断熱型熱量計による標準溶液の純度の不確かさ評価(その3)
断熱型熱量計による標準溶液の純度の不確かさ評価については、簡易解析法をすでに本ホームページ「断熱型熱量計による標準溶液の純度の不確かさ評価」(簡易評価法)で解説しましたが、ここではもう少し突っ込んだ数学モデルを立てて解説することにします。本ホームページ「断熱型熱量計による標準溶液の純度の不確かさ評価(その2)」との違いは「縮分」(reduction)の誤差を考慮したことです。
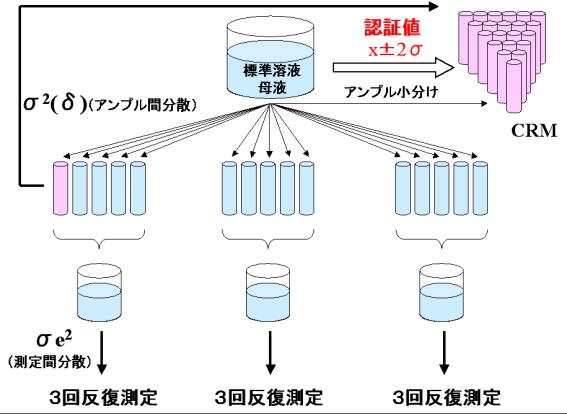
下図のように、CRM(認証標準物質)としてアンプル詰めした標準溶液の純度の認証値を決めるため、断熱型熱量計を用いてアンプル詰めした標準溶液の純度を測定し、アンプル詰めの誤差分散(アンプル間分散)![]() と測定誤差分散(測定間分散)
と測定誤差分散(測定間分散)![]() を求めることにより、認証値
を求めることにより、認証値![]() として必要なCRMアンプル1本の純度
として必要なCRMアンプル1本の純度![]() と標準不確かさ
と標準不確かさ![]() を求めてみましょう。
を求めてみましょう。
調製した標準溶液の母液(純度の(真の)値は母平均![]() とする)から小分けしたアンプル1本(i番目のアンプル)の純度の(真の)値を
とする)から小分けしたアンプル1本(i番目のアンプル)の純度の(真の)値を![]() とすれば
とすれば
![]()
となります。ここで、![]() はアンプルに小分けしたときのアンプル間のバラツキ誤差です。
はアンプルに小分けしたときのアンプル間のバラツキ誤差です。
一方、断熱型熱量計による純度測定はアンプル5本をまとめて1個の被検溶液とするのであるが、その被検溶液は3種類(3種類にグループ分け、すなわち、![]() )作るのであるから、それらのグループの中で
)作るのであるから、それらのグループの中で![]() 番目のグループの
番目のグループの![]() 番目のアンプルの純度の(真の)値を
番目のアンプルの純度の(真の)値を![]() とすれば
とすれば
![]()
となります。ここで、![]() はサンプリングした
はサンプリングした![]() 番目のグループのアンプル間のバラツキ誤差(真値からのカタヨリ)であり、
番目のグループのアンプル間のバラツキ誤差(真値からのカタヨリ)であり、
![]()
と書くことができます。ここで、![]() はグループ間の真値からのカタヨリであり、
はグループ間の真値からのカタヨリであり、![]() はグループ内のバラツキ誤差すなわちアンプル間のバラツキ誤差です。もしグループ分けするときに完全にランダム抽出できていたとすればグループ間の真値からのカタヨリである
はグループ内のバラツキ誤差すなわちアンプル間のバラツキ誤差です。もしグループ分けするときに完全にランダム抽出できていたとすればグループ間の真値からのカタヨリである![]() は限りなく0に近く
は限りなく0に近く![]() は
は![]() のみの成分と考えてよいでしょう。実際、本ホームページの「断熱型熱量計による標準溶液の純度の不確かさ評価」(簡易評価法)ではそのような取り扱いをしています。
のみの成分と考えてよいでしょう。実際、本ホームページの「断熱型熱量計による標準溶液の純度の不確かさ評価」(簡易評価法)ではそのような取り扱いをしています。
したがって、![]() は
は
![]()
となります。ところで、被検溶液はこのようなアンプルを5本まとめて1個の被検溶液としたものであるから、![]() を
を![]() 番目のグループのアンプル5本をまとめて1つにした
番目のグループのアンプル5本をまとめて1つにした![]() 番目の被検溶液にした(縮分した)ときの「縮分」(reduction)誤差とすれば、
番目の被検溶液にした(縮分した)ときの「縮分」(reduction)誤差とすれば、![]() 番目の被検溶液の純度の(真の)値
番目の被検溶液の純度の(真の)値![]() は
は
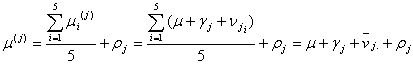
となります。ここで![]() についてはランダムな誤差であるからその期待値と分散は
についてはランダムな誤差であるからその期待値と分散は

とします。また![]() についても同様に
についても同様に

とします。一方、![]() の期待値と分散は
の期待値と分散は
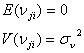
であるから、
![]()
となります。さらに、縮分誤差![]() についてもその期待値と分散は、同様に
についてもその期待値と分散は、同様に

となります。
断熱型熱量計による純度測定は1個の被検溶液について3回の繰り返し測定を行うのであるから、繰り返し番号を![]() とすれば、
とすれば、![]() 番目の被検溶液の純度の測定値
番目の被検溶液の純度の測定値![]() (
(![]() は
は
![]()
となります。ただし、![]() は測定のカタヨリ(被検溶液
は測定のカタヨリ(被検溶液![]() 間のカタヨリ)であり、
間のカタヨリ)であり、![]() は
は![]() 番目の被検溶液についての
番目の被検溶液についての![]() 回目の測定誤差(測定内のバラツキ)です。これら誤差の期待値と誤差はやはり
回目の測定誤差(測定内のバラツキ)です。これら誤差の期待値と誤差はやはり
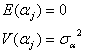
および

とみなします。
したがって、最終的な測定値![]() の完全な数学モデルは
の完全な数学モデルは
![]()
となります。ところで、この式の右辺の![]() 成分の誤差
成分の誤差![]() はお互いに交絡していて通常の統計解析ではそれらの分散
はお互いに交絡していて通常の統計解析ではそれらの分散![]() を区別して算出することはできないので、それらの誤差成分をまとめて
を区別して算出することはできないので、それらの誤差成分をまとめて![]() とすることにします。すなわち
とすることにします。すなわち
![]()
とすると、測定値![]() の数学モデルは
の数学モデルは
![]()
となります。もちろん、この![]() という真値からのカタヨリについてもその期待値と分散は
という真値からのカタヨリについてもその期待値と分散は

と書くことができます。現実問題として、ランダムサンプリングをきちんと行ったとすれば、![]() の成分
の成分![]() の中で
の中で![]() や
や![]() あるいは
あるいは![]() は小さく
は小さく![]() が主成分であると考えることができ、したがって
が主成分であると考えることができ、したがって
![]()
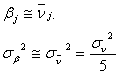
とおくことができます。
この数学モデルは一元配置実験分散分析(1段枝分かれ分散分析)モデルに相当しますので、被検溶液間の変動の水準数(被検溶液の種類の数)を![]() 、測定の繰り返し数を
、測定の繰り返し数を![]() とすれば、ANOVA表は
とすれば、ANOVA表は
|
変動要因 |
水準数 繰り返し数 |
自由度 |
不偏分散 |
期待値 |
|
被検溶液間の変動 |
|
|
|
|
|
被検溶液内の測定誤差変動 |
|
|
|
|
となります。一方、標本の総平均![]() は
は
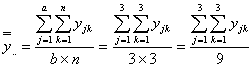
で、これは標準溶液の母液あるいはアンプルあるいは被検溶液の純度の平均値であり、母平均![]() の推定値
の推定値![]() となります。すなわち、
となります。すなわち、
![]()
および
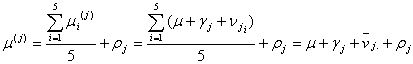
より
![]()
であるから
![]()
であり、よって
![]()
となります。同様に、
![]()
だから
![]()
より、
![]()
となるので
![]()
となります。ただし、 としました。
としました。
したがって、標準溶液の母液のもつ純度の分散![]() は、測定値の総平均値
は、測定値の総平均値![]() の推定値
の推定値![]() と母液の純度の(真の値である)母平均
と母液の純度の(真の値である)母平均![]() との偏差平方和であるから
との偏差平方和であるから

となりますが、![]() と
と![]() は互いに独立で、
は互いに独立で、![]() および
および![]() なので
なので

となります。よって求める母液の純度の標準不確かさ![]() は
は
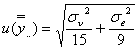
です。
また、アンプル1本当たりの標準不確かさ![]() すなわち
すなわち![]() は、アンプル1本の純度の測定値の推定値
は、アンプル1本の純度の測定値の推定値![]() を測定値の総平均値
を測定値の総平均値![]() とみなせば
とみなせば
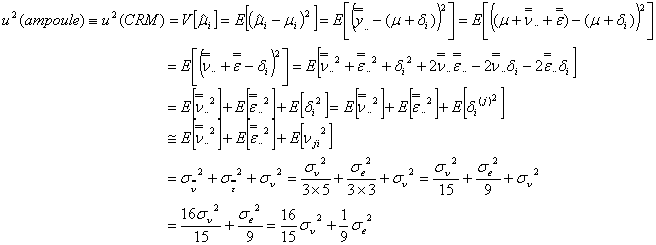
となります。よって、アンプル1本の純度の標準不確かさは
![]()
となります。
よって、求める認証値は
![]()
のようになります。ただし、包含係数![]() としました。
としました。


(参考)いろいろな分散

あるいは
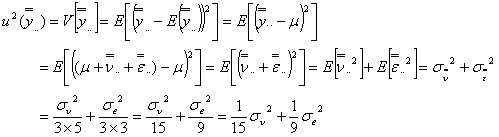
としても求められます。
これは、また、
![]()
であるから、![]() とおけば
とおけば
![]()
となります。あるいは
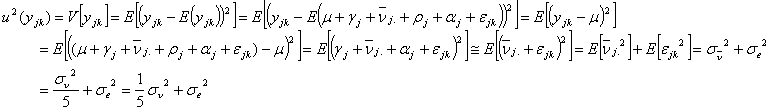
となります。
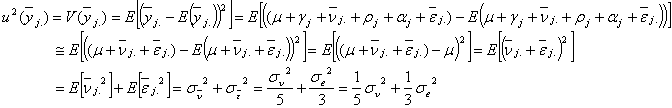
これは、また、
![]()
であるから、![]() とおけば
とおけば
![]()
となります。