断熱型熱量計による標準溶液の純度の不確かさ評価（簡易評価法）

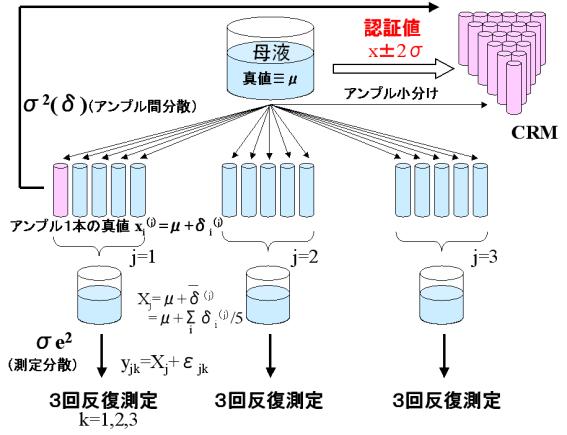
　下図のように、CRM（認証標準物質）としてアンプル詰めした標準溶液の純度の認証値を決めるため、断熱型熱量計を用いてアンプル詰めした標準溶液の純度を測定し、アンプル詰めの誤差分散（アンプル間分散）と測定誤差分散（測定間分散）を求めることにより、認証値として必要なCRMアンプル１本の純度と標準不確かさを求めてみましょう。

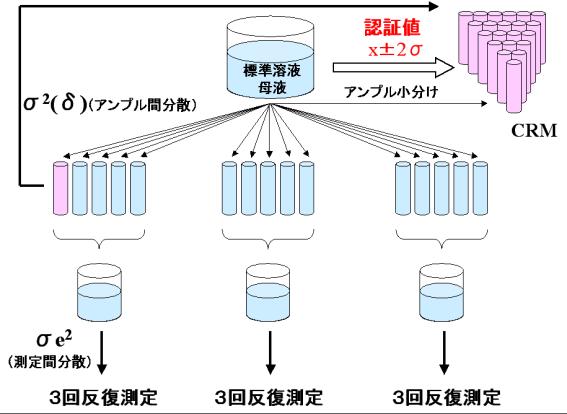
調製した標準溶液の母液（純度の母平均）から小分けしたアンプル1本（i番目のアンプル）の真値をとすれば

となります。ここで、はアンプルに小分けしたときのアンプルのバラツキ誤差です。

　一方、断熱型熱量計による純度測定はアンプル5本をまとめて１個の被検溶液とするのであるが、その被検溶液は3種類作るのであるから、それらの被検溶液の純度の真値をそれぞれとすれば

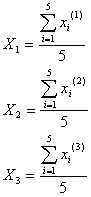
となります。ここで、はに対応する番目のアンプル5本組の中の番目のアンプル中の標準溶液の純度の真値です。すなわち

　断熱型熱量計による純度測定は１個の被検溶液について3回の繰り返し測定を行うのであるから、繰り返し番号をとすれば、番目の被検溶液の測定純度（は

となります。ただし、は番目の被検溶液についての回目の測定誤差です。

　ところで、は、番目の被検溶液のもととなった5本のアンプルのバラツキ誤差の平均値をとすれば、

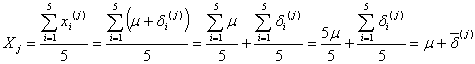
となります。この構造モデルは一元配置実験分散分析（１段枝分かれ分散分析）モデルに相当しますので、自由度と不偏分散の期待値は

変動要因	水準数 繰り返し数	自由度	不偏分散	期待値
被検溶液間の変動
被検溶液内の測定誤差変動

となります。一方、標本の総平均は

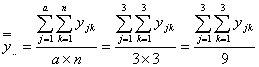
で、これは標準溶液の母液あるいはアンプルあるいは被検溶液の純度の平均値であり、母平均の推定値となります。また、被検溶液１個当たりの分散は

のようにアンプル１本当たりの分散のであるから、上述のANOVA表は

変動要因	水準数 繰り返し数	自由度	不偏分散	期待値
被検溶液間の誤差変動
被検溶液内の測定誤差変動

となります。したがって、標準溶液の母液のもつ標準不確かさは

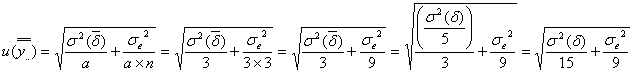
であり、またアンプル１本当たりの標準不確かさすなわちは、上記母液の標準不確かさとアンプル１本に小分けするときの標準不確かさを合成することにより、

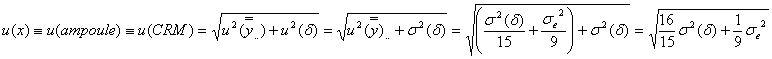
となります。

　よって、求める認証値は

のようになります。ただし、包含係数としました。

（参考）いろいろな分散
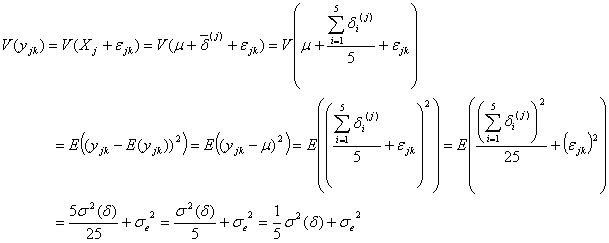
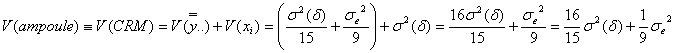
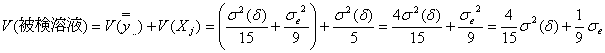